Разложившееся вещество раздражает зрительный нерв в течение некоторого времени, примерно
![]() , секунды. Поэтому возникшее зрительное ощущение сохраняется в течение этого времени, хотя бы само дражание и было очень кратковременным. Эта способность глаза сохранять полученное впечатление в течение указанного времени используется в различных приспособлениях. Самое известное из них — кинематограф.
, секунды. Поэтому возникшее зрительное ощущение сохраняется в течение этого времени, хотя бы само дражание и было очень кратковременным. Эта способность глаза сохранять полученное впечатление в течение указанного времени используется в различных приспособлениях. Самое известное из них — кинематограф.
В кинематографе на экране быстро (24 раза в секунду) сменяется ряд картин (рис. 338), изображающих последовательные положения какого-либо предмета. Глаз сохраняет еще предшествующее изображение, когда он уже начинает получать следующее. В результате восприятие непрерывно меняющихся положений объекта создает впечатление плавного движения.

Рис. 338. Отрезок киноленты. При быстрой смене кадров создается впечатление непрерывно меняющихся положений (движения)
Для получения киноленты необходимо, конечно, осуществлять последовательную съемку движущегося предмета с той же частотой, с которой потом проецируется на экран снятая последовательность фотографий, т. е. 24 раза в секунду. Если скорость проекции будет больше или меньше, чем скорость съемки, то наблюдаемая Картина будет искажена по масштабу времени. Этим пользуются для научных целей. Делая очень частые съемки, например 2000 раз в секунду, и проектируя кадры, например 20 раз в секунду, мы растягиваем явление во времени в сто раз, т. е. наблюдаем его в весьма замедленном темпе. Это позволяет различать подробности в быстро протекающих процессах («лупа времени»). Наоборот, снимая медленный процесс (например, рост кристалла) со значительными промежутками времени и быстро пропуская последовательность снимков, можно воспроизвести в убыстренном темпе и сделать крайне наглядными такие процессы, течение которых обычно незаметно для наблюдателя. Таким образом, например, в последнее время воспроизводят извержение солнечных протуберанцев (применяя ускорение в 500—600 раз).
1. Получите с помощью принципа Гюйгенса закон отражения света.
2.
На рис. 339 дано расположение максимумов интерференционной картины для
![]() . Покажите, что для
. Покажите, что для
![]() линии
линии
![]() будут по-прежнему соответствовать положению максимумов, а линии
будут по-прежнему соответствовать положению максимумов, а линии
![]() дадут положение максимумов.
дадут положение максимумов.
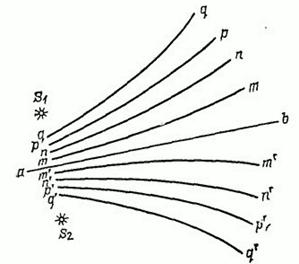
Рис. 339. К упражнению 2: ![]() и
и
![]() — положения когерентных источников света,
— положения когерентных источников света,
![]() - линия симметрии,
- линия симметрии,
![]() - линии максимумов для
- линии максимумов для
![]()
3.
Напомним, что разность хода лучей в тонких пленках впроходящем свете равна
![]() ,, а в отраженном
,, а в отраженном
![]() , где
, где
![]() — толщина пленки, а
— толщина пленки, а
![]() - длина волны в ней. Покажите, что в проходящем свете радиусы светлых колец Ньютона пропорциональны корню квадратному из четных чисел, а радиусы темных — корню квадратному из четных чисел, а радиусы темных – корню квадратному из нечетных чисел; в отраженном же свете — наоборот.
- длина волны в ней. Покажите, что в проходящем свете радиусы светлых колец Ньютона пропорциональны корню квадратному из четных чисел, а радиусы темных — корню квадратному из четных чисел, а радиусы темных – корню квадратному из нечетных чисел; в отраженном же свете — наоборот.
4.
Для опытов с кольцами Ньютона применена плосковыпуклая линза, радиус кривизны которой равен
![]() . а) Определите радиус десятого темного кольца в проходящем и отраженном свете для желтого света
. а) Определите радиус десятого темного кольца в проходящем и отраженном свете для желтого света
![]() . 6) О поделите длину волны зеленой линии ртути, если она дает в отраженном свете второе светлое кольцо с радиусом
. 6) О поделите длину волны зеленой линии ртути, если она дает в отраженном свете второе светлое кольцо с радиусом
![]() в) Определите расстояние между вторыми темными кольцами Ньютона в отраженном свете, относящимися к двум желтым линиям
в) Определите расстояние между вторыми темными кольцами Ньютона в отраженном свете, относящимися к двум желтым линиям
![]() и
и
![]() . г) Которое темное кольцо в отраженном свете зеленой линии меди
. г) Которое темное кольцо в отраженном свете зеленой линии меди
![]() имеет радиус
имеет радиус
![]() ?
?
5.
Каков радиус кривизны линзы в опыте Ньютона, если красная линия водорода
![]() дает в проходящем свете восьмое светлое кольцо с радиусом
дает в проходящем свете восьмое светлое кольцо с радиусом
![]() ?
?
6.
Физо, наблюдая кольца Ньютона в желтом свете линии натрия, обнаружил, что четкость картины постепенно уменьшается по мере увеличения номера
![]() кольца. При
кольца. При
![]() наблюдалось полное смазывание интерференционной картины, т.е. не наблюдалось резких максимумов, разделенных минимумами. Однако при переходе к большим кольцам
наблюдалось полное смазывание интерференционной картины, т.е. не наблюдалось резких максимумов, разделенных минимумами. Однако при переходе к большим кольцам
![]() обнаруживается вновь улучшение четкости. Объяснение этого явления связано с тем, что желтый свет натрия соответствует двум близким линиям
обнаруживается вновь улучшение четкости. Объяснение этого явления связано с тем, что желтый свет натрия соответствует двум близким линиям
![]() и
и
![]() . Объясните явление. Известно, что
. Объясните явление. Известно, что
![]() ; определите из указанных наблюдений
; определите из указанных наблюдений
![]() . При каком
. При каком
![]() четкость картины будет вновь наибольшей?
четкость картины будет вновь наибольшей?
7.
Между двумя стеклянными пластинками зажата с одной стороны проволочка, диаметр которой
![]() (рис. 340), так что образуется воздушный клин. Длина пластинки
(рис. 340), так что образуется воздушный клин. Длина пластинки
![]() . а вид будет иметь интерференционная картина? Какой вид будет иметь интерференционная картина? Каково будет в стояние между соседними темными линиями, если пластинка освещена зеленым светом ртутной лампы
. а вид будет иметь интерференционная картина? Какой вид будет иметь интерференционная картина? Каково будет в стояние между соседними темными линиями, если пластинка освещена зеленым светом ртутной лампы
![]() ? Как изменится ширина полос (расстояние между соседними максимумами) при увеличении утла между пластинками (увеличение
? Как изменится ширина полос (расстояние между соседними максимумами) при увеличении утла между пластинками (увеличение
![]() или уменьшение
или уменьшение
![]() ).
).

Рис. 340. К упражнению 7
8. На основании результатов упражнения 7 объясните, почему в случае, изображенном на рис.266, интерференционные полосы сужаются к нижней части пленки.
9.
Для расположения, изображенного на рис. 340, известно, что
![]() и
и
![]() . Сколько интерференционных полос уложится на поверхности стеклянной пластинки. Как зависит число полос от толщины зазора
. Сколько интерференционных полос уложится на поверхности стеклянной пластинки. Как зависит число полос от толщины зазора
![]() ? Как зависит число полос от размера пластинки?
? Как зависит число полос от размера пластинки?
10. Два когерентных источника
![]() и
и
![]() расположены на расстоянии
расположены на расстоянии
![]() друг от друга. На экране, расположенном на расстоянии
друг от друга. На экране, расположенном на расстоянии
![]() от источников, наблюдаются полосы интерференции (рис. 341). Рассчитайте ширину интерференционной полосы, т. е. расстояние
от источников, наблюдаются полосы интерференции (рис. 341). Рассчитайте ширину интерференционной полосы, т. е. расстояние
![]() между соседними максимумами, если длина волны равна
между соседними максимумами, если длина волны равна
![]() . Расстояние
. Расстояние
![]() велико по сравнению с
велико по сравнению с
![]() и
и
![]() . Положения максимумов на экране соответствует точками, разность расстояний от которых до
. Положения максимумов на экране соответствует точками, разность расстояний от которых до
![]() и
и
![]() равна целому числу длин волн.
равна целому числу длин волн.
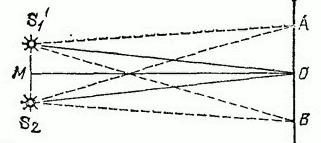
Рис. 341. К упражнению 10: расстояние ![]()
11.
Перед двойной призмой (бипризмой), тупой угол которой близок к
![]() , расположен точечный источник света
, расположен точечный источник света
![]() . Покажите, что пучки, преломленные обеими половинами бипризмы, интерферируют так, как если бы они исходили из двух когерентных источников
. Покажите, что пучки, преломленные обеими половинами бипризмы, интерферируют так, как если бы они исходили из двух когерентных источников
![]() и
и
![]() (рис.342). Рассчитайте расстояние
(рис.342). Рассчитайте расстояние
![]() между этими когерентными источниками, если тупой угол бипризмы равен
между этими когерентными источниками, если тупой угол бипризмы равен
![]() ; расстояние
; расстояние
![]() от
от
![]() до бипризмы равно
до бипризмы равно
![]() , и показатель преломления стекла бипризмы равен 1,5. обратите внимание на то, что углы
, и показатель преломления стекла бипризмы равен 1,5. обратите внимание на то, что углы
![]() и
и
![]() призмы очень малы.
призмы очень малы.
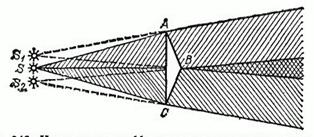
Рис. 342. К упражнению 11: для ясности чертежа углы ![]() и
и
![]() бипризмы сильно преувеличены; пучки лучей, идущих на нижнюю и верхнюю половины бипризмы, заштрихованы различно
бипризмы сильно преувеличены; пучки лучей, идущих на нижнюю и верхнюю половины бипризмы, заштрихованы различно
12.
В качестве источника
![]() в предыдущей задаче использована тонкая щель, параллельная ребру призмы и освещенная желтым светом натрия
в предыдущей задаче использована тонкая щель, параллельная ребру призмы и освещенная желтым светом натрия
![]() . Интерференция наблюдается на экране, расположенном на расстоянии
. Интерференция наблюдается на экране, расположенном на расстоянии
![]() от
от
![]() . Покажите, что центральный максимум интерференции лежит в том месте, где продолжение линии
. Покажите, что центральный максимум интерференции лежит в том месте, где продолжение линии
![]() (рис. 342) пересекает экран. Найдите положение на экране других максимумов и минимумов. Вычислите ширину интерференционной полосы, т.е. расстояние между соседними максимумами (или минимумами). Как она будет меняться при уменьшении тупого угла бипризмы; при увеличении расстояния до экрана?
(рис. 342) пересекает экран. Найдите положение на экране других максимумов и минимумов. Вычислите ширину интерференционной полосы, т.е. расстояние между соседними максимумами (или минимумами). Как она будет меняться при уменьшении тупого угла бипризмы; при увеличении расстояния до экрана?
13. В задачах 10 и 11 показано, что ширина интерференционных полос тем больше, чем меньше расстояние между двумя когерентными источниками.
Интерференцию при отражении от тонкой пленки можно рассчитать как интерференцию от двух когерентных источников, представляющих собой отражение источника света в верхней и нижней поверхностях пленки. Как изменится ширина полос, если пленка станет толще?
14.
Выведите формулы для радиуса первой и второй зон Френеля для точки, отстоящей на расстоянии
![]() от фронта плоской волны, длина которой равна
от фронта плоской волны, длина которой равна
![]() .
.
15.
Рассчитайте площадь первой, второй и третьей зон Френеля для точки, отстоящей на расстоянии
![]() от фронта плоской волны, если длина волны равна
от фронта плоской волны, если длина волны равна
![]() .
.
16.
Какая длина волны максимума третьего порядка дифракционной решетки совпадает с максимумом четвертого порядка для длины волны
![]() ?
?
17.
Для каких длин волн можно наблюдать дифракционные максимумы с решеткой, период которой равен
![]() ?
?
18.
На дифракционную решетку с периодом
![]() падает монохроматический свет, длина волны которого равна
падает монохроматический свет, длина волны которого равна
![]() . Спектры наблюдаются с помощью трубы, как показано на рис. 343. Сколько порядков спектров можно наблюдать? Дайте общее решение; примените его для частного случая, когда
. Спектры наблюдаются с помощью трубы, как показано на рис. 343. Сколько порядков спектров можно наблюдать? Дайте общее решение; примените его для частного случая, когда
![]() , а
, а
![]() .
.
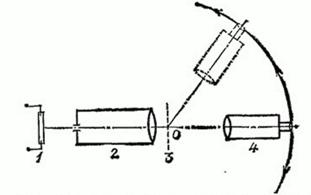
Рис. 343. к упражнению 18: 1 – источник монохроматического света, 2 – коллиматор, 3 – дифракционная решетка, 4 – труба, которую можно вращать около центра ![]()
19.
Сколько штрихов на миллиметр должна иметь дифракционная решетка, пригодная для исследований инфракрасных спектров с длиной волны около
![]() .
.
20.
Выведите для дифракционной решетки соотношение между длинами волн максимумов
![]() и
и
![]() порядков, которые совпадают друг с другом.
порядков, которые совпадают друг с другом.
Рассмотрите для дифракционной решетки: а) линии каких длин волн спектра второго порядка и спектра третьего порядка накладываются на линию длины волны
![]() спектра первого порядка; б) линии какой длины волны спектра первого порядка накладываются на линию длины волны
спектра первого порядка; б) линии какой длины волны спектра первого порядка накладываются на линию длины волны
![]() спектра второго порядка.
спектра второго порядка.
21.
Дифракционная решетка имеет 100 штрихов на миллиметр. Определите углы, под которыми расположены максимумы первого, второго и третьего порядков для
![]() .
.
22.
Дифракционный спектроскоп имеет устройство, изображенное на рис.344. Период решетки равен
![]() , фокусное расстояние объектива 3 равно
, фокусное расстояние объектива 3 равно
![]() . а) Определите расстояние между двумя желтыми линиями натрия
. а) Определите расстояние между двумя желтыми линиями натрия
![]() и
и
![]() в первом и втором порядках. б) Определите расстояние между положениями линии
в первом и втором порядках. б) Определите расстояние между положениями линии
![]() в спектрах первого и второго порядков, в) В каком порядке расстояние между двумя желтыми линиями ртути
в спектрах первого и второго порядков, в) В каком порядке расстояние между двумя желтыми линиями ртути
![]() и
и
![]() будет Раино
будет Раино
![]() ? г) Дисперсия спектроскопа измеряется числом нанометров приходящихся на участок пластинки длиной в
? г) Дисперсия спектроскопа измеряется числом нанометров приходящихся на участок пластинки длиной в
![]() . Зависит ли дисперсия дифракционного спектроскопа от длины волны? Вычислите дисперсию спектроскопа для первого и второго порядков.
. Зависит ли дисперсия дифракционного спектроскопа от длины волны? Вычислите дисперсию спектроскопа для первого и второго порядков.
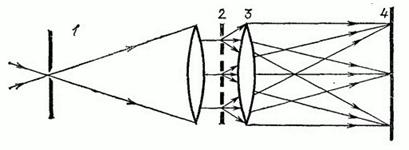
Рис. 344. К упражнению 22: 1 – коллиматор, 2 – дифракционная решетка, 3 – объектив камеры, 4 — фотопластинка
23. Если смотреть, прищурив глаз, на нить лампочки накаливания, то нить кажется окаймленной светлыми бликами по двум перпендикулярным направлениям. При поворачивании головы около луча зрения картина также поворачивается. Если нить лампы расположена примерно параллельно носу наблюдателя, то удается наблюдать ряд цветных (радужных) изображений нити; это не удается лишь очень неотчетливо, если нить лампы расположена перпендикулярно к носу наблюдателя.
Выполните эти наблюдения.
Обратите внимание, в каком порядке расположены цвета в цветном изображении.
Объясните наблюдаемые явления.
24.
Принимая в предыдущей задаче толщину волосков ресниц, равной
![]() , и считая, что волоски отстоят друг от друга на
, и считая, что волоски отстоят друг от друга на
![]() , рассчитайте примерное расстояние между изображениями нити лампы, если она находится в
, рассчитайте примерное расстояние между изображениями нити лампы, если она находится в
![]() от наблюдателя. Изменяется ли это расстояние при приближении и удалении лампы? Проверьте последнее заключение на опыте.
от наблюдателя. Изменяется ли это расстояние при приближении и удалении лампы? Проверьте последнее заключение на опыте.
25. Более точная схема расположения приборов при определении скорости света по методу Фуко приведена на рис. 345.
Линза дает изображение источника
![]() на поверхности сферического зеркала, центр которого совпадает с осью вращения зеркала. Стеклянная пластинка, отражая часть света в направлении
на поверхности сферического зеркала, центр которого совпадает с осью вращения зеркала. Стеклянная пластинка, отражая часть света в направлении
![]() , облегчает выполнение наблюдений. Рассмотрите как работает эта схема.
, облегчает выполнение наблюдений. Рассмотрите как работает эта схема.
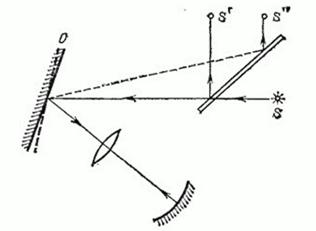
Рис. 345. К упражнению 25
26.
Разрешающая способность телескопа такова, что две звезды, угловое расстояние между которыми равно
![]() , различаются в этот телескоп как раздельные. На каком расстоянии (в
, различаются в этот телескоп как раздельные. На каком расстоянии (в
![]() ) должны находиться друг от друга такие различимые звезды, если свет от них идет до Земли 100 световых лет?
) должны находиться друг от друга такие различимые звезды, если свет от них идет до Земли 100 световых лет?
27.
Разрешающая способность глаза при достаточной освещенности объекта равна
![]() . На расстоянии
. На расстоянии
![]() от глаза на белом фоне натянуты тонкие черные проволочки. Каково должно быть расстояние между проволочками, чтобы они не сливались для глаза?
от глаза на белом фоне натянуты тонкие черные проволочки. Каково должно быть расстояние между проволочками, чтобы они не сливались для глаза?
28. Почему близорукий глаз может различать более мелкие детали (например, читать более мелкий шрифт), чем нормальный глаз?
29.
Диаметр объектива микроскопа близок к диаметру в глаза. Поэтому их угловая разрешающая сила, обусловленная дифракцией на отверстии зрачка или объектива, примерно одинакова и равна
![]() . Но так как фокусное расстояние объектива мало, то рассматриваемый объект можно сильно приблизить к объективу. На каком расстоянии должны быть штрихи сетки, чтобы их можно было различить в микроскоп, фокусное расстояние объектива которого равно
. Но так как фокусное расстояние объектива мало, то рассматриваемый объект можно сильно приблизить к объективу. На каком расстоянии должны быть штрихи сетки, чтобы их можно было различить в микроскоп, фокусное расстояние объектива которого равно
![]() ?
?
30.
Разрешающая способность глаза (острота зрения) зависит от освещенности и характера рассматриваемого объекта. Нормальный глаз при освещенности около
![]() может различать на черном фоне детали белого объекта (например, буквы, написанные мелом на черной доске), если угловые размеры их около
может различать на черном фоне детали белого объекта (например, буквы, написанные мелом на черной доске), если угловые размеры их около
![]() . Какого размера должны быть буквы на классной доске, чтобы ученик мог их различать, с парты, расположенной на расстоянии
. Какого размера должны быть буквы на классной доске, чтобы ученик мог их различать, с парты, расположенной на расстоянии
![]() от доски? Детали, отличающие одну букву от другой, составляют примерно пятую часть буквы.
от доски? Детали, отличающие одну букву от другой, составляют примерно пятую часть буквы.
31.
На каком расстоянии должны быть два пункта на Луне (например, две горные вершины), чтобы они не сливались при наблюдении глазом и с помощью телескопа? Освещенность и контрастность предполагаются достаточными для того, чтобы можно было для глаза считать разрешающую способность равной
![]() , а для телескопа
, а для телескопа
![]() . Расстояние до Луны равно
. Расстояние до Луны равно
![]() .
.
32. Лист белой бумаги освещен одновременно двумя электрическими дугами, перед одной из них стоит желтое стекло, а перед другой — синее (рис. 346, а). Желтое стекло поглощает голубую, синюю и фиолетовую части спектра, а синее стекло — красную, оранжевую и желтую.
Тот же лист бумаги, ярко освещенный электрической дугой, рассматривает через те же два цветных стекла — желтое и синее, сложенное вместе (рис. 346, б). Объясните, какой будет казаться освещенная бумага в первом и втором случаях.
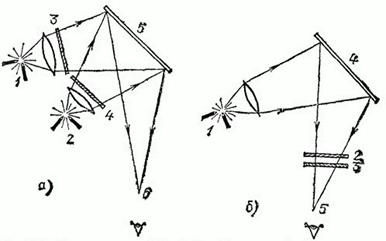
Рис. 346. К упражнению 32: а) 1 и 2 – дуги, 3-4 – желтое и синее стекла, 5 – белая бумага, 6 – глаз; б) 1 – дуга, 2-3 – желтое и синее стекла, 4 – белая бумага, 5 – глаз
33. Опишите, как выглядит белая, красная, желтая, зеленая и синяя бумага, освещенная желтым светом натриевого пламени,
34. Объясните происхождение света: а) синего неба, б) синего стекла, в) синей бумаги.
35.
На пластинку никеля, для которого работа выхода равна
![]() , падает ультрафиолетовое излучение, длина волны которого равна
, падает ультрафиолетовое излучение, длина волны которого равна
![]() . Определите максимальную скорость фотоэлектронов.
. Определите максимальную скорость фотоэлектронов.
Значения необходимых постоянных: масса электрона равна
![]() , скорость света равна
, скорость света равна
![]() , постоянная Планка равна
, постоянная Планка равна
![]() .
.
36.
Какова наибольшая длина волны света, под действием которой можно получить фотоэффект с поверхности натрия (работа выхода
![]() ), вольфрама
), вольфрама
![]() , платины
, платины
![]() ? Эта длина волны носит название длинноволновой или красной границы фотоэффекта.)
? Эта длина волны носит название длинноволновой или красной границы фотоэффекта.)
37.
Под действием ренгеновского излучения пластинка из
![]() , изображенная на рис. 330, зарядилась так, что электрометр показывает
, изображенная на рис. 330, зарядилась так, что электрометр показывает
![]() . 1) Каков знак заряда электрометра? 2) Какова длина волны рентгеновского излучения, примененного в этом опыте? б) Изменится ли заметно результат опыта, если пластинку сделать из никеля или вольфрама?
. 1) Каков знак заряда электрометра? 2) Какова длина волны рентгеновского излучения, примененного в этом опыте? б) Изменится ли заметно результат опыта, если пластинку сделать из никеля или вольфрама?
38. Вычислите отношение путей солнечных лучей в атмосфере для положения Солнца на горизонте и в зените (ср. рис.319).
Рассмотрите атмосферу как имеющую равномерную плотность, равную плотности у поверхности Земли (так называемая приведенная атмосфера). Ее толщину примите равной
![]() , а радиус Земли
, а радиус Земли
![]() .
.
39. Нередко замечается, что классная доска «отсвечивает» т.е. написанное белым мелом неразличимо на черной доске. Объясните это явление. При каких положениях учеников, доски и окна оно будет наблюдаться? Будет ли отсвечивать экран, сделанный из черного бархата?
Примечание. Буквы, написанные мелом, отражают свет диффузно (рассеивают) и обладают большим коэффициентом отражения (альбедо для мела близко к единице); черная лакированная доска отражает зеркально, хотя и с небольшим коэффициентом отражения; это коэффициент отражения заметно возрастает по мере приближения угла падения света на доску к прямому.
40. Даны два фильтра: фиолетовый и желто-зеленый; первый пропускает фиолетовую и темно-синюю часть спектра, а второй — красную, оранжевую, желтую и желто-зеленую. Сложенные вместе, они задерживают, следовательно, все цвета спектра. Такие фильтры называются дополнительными.
Свет от электрической дуги направляется на белую бумагу или на сосуд с флюоресцеином, причем фильтры располагаются в одном из четырех положений, изображенных на рис. 347.
Что мы будем наблюдать в первом (бумага) и втором (флюоресцеин) случаях?
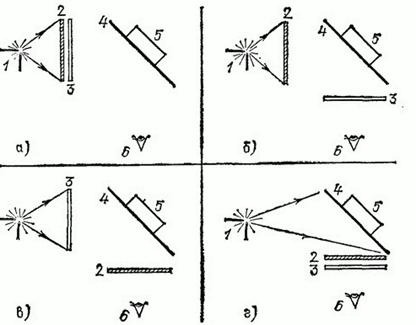
Рис. 347. К упражнению 40: 1 — дуга, 2 — фиолетовый фильтр, 3 — желто-зеленый фильтр, 4 — лист бумаги, 5 — сосуд с флюоресцеином, 6 — глаз











Комментарии: (0)