Динамическая вязкость и коэфециент внутреннего трения

Про динамическую вязкость ( далее по тексту — ДВ )и коэфециент внутреннего трения ( далее по тексту — КВТ )
Очевидно что они оба описывают суть один и тот же процесс — сцепление условных «слоев» материала, т.е. и проявляются они в равной степени как на газы с жидкостями, так и на сыпучие грунты с твердыми телами. В качестве очевидных примеров: тела с плотностью выше среды тонут, а с меньшей- всплывают как в жидкостях/газах, так и в грунтах; градиент скоростей при движении одной плоскости относительно другой
А значит вполне рационально предположить, что ДВ, как и КВТ, помимо всего прочего, описывает ещё и угол естественного откоса.
Т.е. если налить километровую лужу воды на поверхности в любой точке перпендикулярной гравитации, то в середине получится превышение уровня глубины по кроям около полуметра ( если предположить, что 1 Па*с эквивалентен единичному КВТ )
Вопрос номер раз — насколько реально поставить эксперимент подтверждающий или опровергающий это? Насколько обоснован такой вывод ?
Суть дела вобщем в том, что хочу запрограммировать алгоритм поведения материалов для условной " песочнецы " и было бы здорово, если бы поведение всех материалов расчитывалось одним и тем же макаром, а не набором отдельных методов для каждого.
Заранее спасибо

#69105 Рейстлин :Про динамическую вязкость ( далее по тексту — ДВ )и коэфециент внутреннего трения ( далее по тексту — КВТ )
Коэффициент!!! Знаете, такие ошибки (да ещё дважды повторенные) сильно снижают желание отвечать.
В качестве очевидных примеров: тела с плотностью выше среды тонут, а с меньшей- всплывают как в жидкостях/газах, так и в грунтах;
К внутреннему трению (вязкости) это никакого отношения не имеет. Имеет отношение только к плотности материалов.
А значит вполне рационально предположить, что ДВ, как и КВТ, помимо всего прочего, описывает ещё и угол естественного откоса.
Ничего рационального тут нет.
Т.е. если налить километровую лужу воды на поверхности в любой точке перпендикулярной гравитации,
Точка не может быть перпендикулярна ничему. Тем более гравитации.
то в середине получится превышение уровня глубины по кроям около полуметра
«Уровень глубины» — это круто. У вас какой язык родной?
Нет. Поверхность жидкости в статике (то есть без движения) всегда эквипотенциальна. Это следует из того, что у жидкостей (и газов) отсутствует трение покоя.
Вопрос номер раз — насколько реально поставить эксперимент подтверждающий или опровергающий это?
Элементарно. Взять бассейн длиной 1 км (такие есть, например, опытовый бассейн в инстиитуте Крылова (его длина ровно одна морская миля, 1852 метра, в нём модели кораблей таскают для определения мореходных характеристик; да вы должны это знать, раз из Санкт-Петербурга) и посветить над поверхностью воды лазерной указкой.
Насколько обоснован такой вывод ?
Совершенно необоснован.
Суть дела вобщем в том, что хочу запрограммировать алгоритм поведения материалов для условной " песочнецы "
Песочницы!!!
При вашем нынешнем уровне знания физики программировать имитатор физических процессов абсолютно бессмысленно.

#69110 zam :
Трения покоя может и нет, но трение покоя все-таки про систему тело-жищкость
Связь между молекулами, обуславливающую вязкость есть, а значит в определённый момент силы, препятствующие смещению частицы при некоторых давлении ( создаваемом атмосферой и верхним слоями жидкости ) , скорости и угле откоса, на последнюю могут оказаться равны или больше сил, вынуждающих частицу занимать новое местоположение. Т.е. скорость течения окажется настолько низкой , что можно будет утверждать, что жидкость статична и сохраняет некоторый угол поверхности.
Перпендикулярна не точка, а поверхность в любой точке ( как и написано ). И что вам не нравится в " уровне глубины "? Не придирайтесь к формулировкам и правописанию.

#69258 Рейстлин :можно будет утверждать, что жидкость статична и сохраняет некоторый угол поверхности.
Нельзя.
Перпендикулярна не точка, а поверхность в любой точке ( как и написано ).
Написано "на поверхности в любой точке перпендикулярной гравитации".
Если грамотно написать то, что вы имеете в виду, то получится: «на поверхности, которая в любой точке перпендикулярна вектору силы тяжести».
И что вам не нравится в " уровне глубины "? Не придирайтесь к формулировкам и правописанию.
А почему вы не хотите писать грамотно?

#69263 zam
Почему же нельзя ?
Мы же утверждаем, что стекло — статично, хотя на самом деле оно квазитекуче и имеет некоторую вязкость
На счёт грамотности письма: мысль приходит не в словах и не говорит как её " грамотно " написать, но эт все не суть дела

#69278 Рейстлин :#69263 zamПочему же нельзя ?
Мы же утверждаем, что стекло — статично, хотя на самом деле оно квазитекуче и имеет некоторую вязкость
Нет. Стекло — это не жидкость. Нынче к трём традиционным агрегатным состояниям вещества (твёрдое, жидкое, газообразное) часто добавляют четвёртое — стеклообразное (правда, это пока не общепринято).
Но даже если считать, что стекло квазитекучее с огромной вязкостью, то нужно дождаться, когда течение прекратится (возможно, сотни лет).

#69378 zam
На счёт лазерной указки :
Эксперимент не пройдёт. Если допустить, что земля — шар, направление силы тяжести лежит к центру шара , а поверхность жидкости эквипотенциальна, то луч пущенный ровно над поверхностью воды пересечется с ее поверхностью. 2 см высоты от хорды до дуги на 1 км хорды дадут о себе знать.
На счёт трения покоя :
А адгезия не учитывается? Капли и тонкие слои жидкостей отлично держатся до некоторых наклона и массы на поверхности. И силу, удерживающую каплю вполне можно учитывать в качестве составляющей ее силы трения покоя.

#69468 Рейстлин :#69378 zamНа счёт лазерной указки :
Эксперимент не пройдёт. Если допустить, что земля — шар, направление силы тяжести лежит к центру шара , а поверхность жидкости эквипотенциальна, то луч пущенный ровно над поверхностью воды пересечется с ее поверхностью. 2 см высоты от хорды до дуги на 1 км хорды дадут о себе знать.
Именно эти 2 сантиметра и можно измерить таким способом.
На счёт трения покоя :
А адгезия не учитывается? Капли и тонкие слои жидкостей отлично держатся до некоторых наклона и массы на поверхности. И силу, удерживающую каплю вполне можно учитывать в качестве составляющей ее силы трения покоя.
Это давно известно:
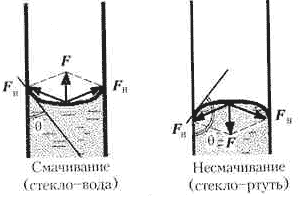
Но вы же про угол естественного откоса (то есть без подпорок).

https://school-science.ru/8/11/42439 Плазма- четвертое состояние вещества

#69105 Рейстлин :Вопрос номер раз — насколько реально поставить эксперимент подтверждающий или опровергающий это? Насколько обоснован такой вывод ?
Заранее спасибо
Ответа на ваш вопрос нет. Т.к. вопроса нет.
Налитая в луже вода находится в статике и сила поверхностного натяжения, которая у вас формиркет привышение лужи в центре над ее краями — сродни трению покоя.
А динамическая вязкость в жидкостях — это во время движения и она сродни трению скольжения.
Трение скольжения всегда меньше трения покоя.
Более того при движении воды или воздуха при увеличении скорости давление падает и динамическая вязкость тоже.
Более того при движении воды или воздуха при увеличении скорости растет температура и динамическая вязкость падает еще больше.
Поэтому вам для начала надо определиться про что вы ведете речь, про динамику или про статику.
— — — —
А вот что вы понимаете под коэффициентом внутреннего трения? Это вообще загадка. Это что у вас?
Дело в том, что в физике «коэффициентом внутреннего трения» и «динамическая вязкость» — это одно и тоже. А у вас?
По хорошему, ваша тема должна быть озвучена вот так: «Динамическая вязкость (коэфециент внутреннего трения)».
Предположим у вас есть поток воздуха со скоростью 30м/сек, температура внутри потока +30°....… так в чем у вас вопрос?
отредактировал(а) Pavel_M: 2025-07-07 15:35 GMT





