Почему Луна не падает на Солнце?

#69032 Fedor :#69023 zam :То, что вы ни разу не подтвердили свои слова ссылками на учебники о чём свидетельствует?
Это свидетельствует о том, что я излагаю собственные соображения по обсуждаемому вопросу,
Чтобы иметь собственные соображения, нужно уметь соображать.
Тот, кто это умеет, обязательно захочет сравнить результаты своих соображений с результатами других. И, в случае расхождения, постарается разобраться, у кого ошибка.
Вы не цитируете учебников по той причине, что любая цитата покажет, что вы врёте.
а не лезу в Википедию, чтобы скопировать чье -то мнение, не понимая сути проблемы.
Так попробуйте понять проблему и с этим пониманием слазить в Вики и узнать, как эта проблема решается. Чего сложного-то?
Я приготовил простенькую иллюстрацию к задаче, в которой одновременно присутствуют декартова и полярная системы координат, естественно, системы неподвижные, но Луна в них движется.
Прекрасно! А теперь при помощи вашей крайне содержательной картинки запишите уравнение движения Луны в декартовых и полярных координатах.
Ваши картинки снова не раскрываются.
Подозреваю, что вы опять врёте. У меня всё открывается и на стационарном компьютере, тремя разными браузерами, и на телефоне. Без проблем.
Напишите простыми словами результат решения по пункту 2. Какие там силы, скорости и ускорения?
Пункт 2.
Движение с постоянной по величине скоростью по окружности с центром в начале координат и радиусом R.
В этом случае:
— закон движения тела: \(r\left( t \right)=R=const,\varphi\left( t \right) — произвольная\; функция\) ;
— скорость радиальная: \(v_r=0\) ;
- скорость поперечная (там она так называется, обычно тангенциальная): \(v_p=R\dot{\varphi}\) ;
— модуль скорости \(v=R \left| \dot{\varphi} \right|\) ;
— ускорение радиальное: \(a_r=-R\dot{\varphi}^2\) ;
— ускорение поперечное: \(a_p=R\ddot{\varphi}\) .
— модуль ускорения: \(a=R \sqrt{\dot{\varphi}^4+\ddot{\varphi}^2}\) .
Про силы там ничего нет, потому что лекция про кинематику.
Отсюда, если движение по окружности с постоянной по модулю линейной скоростью, то:
— закон движения тела: \(r\left( t \right)=R=const,\varphi\left( t \right)= \omega t\) ;
— скорость радиальная: \(v_r=0\) ;
- скорость поперечная : \(v_p=\omega R\) ;
— модуль скорости \(v=\omega R\) ;
— ускорение радиальное: \(a_r=- \omega ^2 R\) ;
— ускорение поперечное: \(a_p=0\) .
— модуль ускорения: \(a= \omega ^2R \) .
Уравнения движения произвольной точки в полярных координатах в зависимости от условий ее движения можно выразить через ее координаты, скорость и ускорение.
Ну так выражайте!
Но! Мы рассматриваем конкретный случай – движение Луны. Радиальные скорость и ускорение равны нулю. Угловая скорость постоянна. Вот такие результаты должны следовать из приводимых Вами формул.
Враньё. Радиальное ускорение не равно нулю.
Уравнения движения Луны в декартовых и полярных координатах написаны в приведенных выше текстах.
Вы ничего не написали, кроме вранья.
отредактировал(а) zam: 2025-03-19 15:48 GMT

#69034 zam :#69032 Fedor :Подозреваю, что вы опять врёте. У меня всё открывается и на стационарном компьютере, тремя разными браузерами, и на телефоне. Без проблем.
Можете не верить – это Ваше право.
Напишите простыми словами результат решения по пункту 2. Какие там силы, скорости и ускорения?
Пункт 2.
Движение с постоянной по величине скоростью по окружности с центром в начале координат и радиусом R.
В этом случае:
— закон движения тела: \(r\left( t \right)=R=const,\varphi\left( t \right) — произвольная\; функция\) ;
Для случая Луны ф(t) – не произвольная функция, а ф(t)=Vt/R+c, V=const
— скорость радиальная: \(v_r=0\) ;
Если радиальная скорость равна нулю – величина постоянная, то производная по времени от нее (радиальное ускорение) тоже равно нулю – азбучная истина.
- скорость поперечная (там она так называется, обычно тангенциальная): \(v_p=R\dot{\varphi}\) ;
Да, V=Rdф/dt.
— модуль скорости \(v=R \left| \dot{\varphi} \right|\) ;
— ускорение радиальное: \(a_r=-R\dot{\varphi}^2\) ;
Формально так, но так как dф/dt=const, вторая производная по времени от нее равна нулю и следовательно радиальное ускорение равно нулю.
— ускорение поперечное: \(a_p=R\ddot{\varphi}\) .
Формально так, но так как dф/dt=const, вторая производная по времени от нее равна нулю.
Это же самое я Вам говорил и говорю многократно.
Я оказался прав. Вы не поняли текста, на который ссылаетесь.

#69036 Fedor :#69034 zam :#69032 Fedor :Подозреваю, что вы опять врёте. У меня всё открывается и на стационарном компьютере, тремя разными браузерами, и на телефоне. Без проблем.
Можете не верить – это Ваше право.
Конечно. В данном случае я проверить не могу. Просто ваше кредо: «Враньё, только враньё, ничего, кроме вранья».
Напишите простыми словами результат решения по пункту 2. Какие там силы, скорости и ускорения?
Пункт 2.
Движение с постоянной по величине скоростью по окружности с центром в начале координат и радиусом R.
В этом случае:
— закон движения тела: \(r\left( t \right)=R=const,\varphi\left( t \right) — произвольная\; функция\) ;
Для случая Луны ф(t) – не произвольная функция, а ф(t)=Vt/R+c, V=const
Это несколькими строками ниже разобрано (за пределами цитаты из лекции)..
— скорость радиальная: \(v_r=0\) ;
Если радиальная скорость равна нулю – величина постоянная, то производная по времени от нее (радиальное ускорение) тоже равно нулю – азбучная истина.
Радиальное ускорение не есть производная от радиальной скорости. Откуда вы эту чушь взяли (да ещё обозвали её азбучной истиной)?
- скорость поперечная (там она так называется, обычно тангенциальная): \(v_p=R\dot{\varphi}\) ;
Да, V=Rdф/dt.
— модуль скорости \(v=R \left| \dot{\varphi} \right|\) ;
— ускорение радиальное: \(a_r=-R\dot{\varphi}^2\) ;
Формально так, но так как dф/dt=const, вторая производная по времени от нее равна нулю и следовательно радиальное ускорение равно нулю.
В выражение для радиального ускорения вторая производная от угла \(\varphi\) не входит. Для произвольного движения \(a_r=\ddot r — r \dot \varphi ^2\) , для равномерного движения по окружности \(a_r= — R \dot \varphi ^2\) .
— ускорение поперечное: \(a_p=R\ddot{\varphi}\) .
Формально так, но так как dф/dt=const, вторая производная по времени от нее равна нулю.
Что и написано в моём сообщении.
Это же самое я Вам говорил и говорю многократно.
Вы непрерывно врёте. Как в этот раз, так и всегда.
Я оказался прав. Вы не поняли текста, на который ссылаетесь.
Где же вы оказались правы, когда всё ошибочно?

#69040 zam :#69036 Fedor :— ускорение радиальное: \(a_r=-R\dot{\varphi}^2\) ;
Формально так, но так как dф/dt=const, вторая производная по времени от нее равна нулю и следовательно радиальное ускорение равно нулю.
Результат невнимательного прочтения текста.
В выражение для радиального ускорения вторая производная от угла \(\varphi\) не входит. Для произвольного движения \(a_r=\ddot r — r \dot \varphi ^2\) , для равномерного движения по окружности \(a_r= — R \dot \varphi ^2\) .
Если вторая производная радиуса участвует в произвольном движении, то она должна участвовать и в равномерном движении по окружности. Для случая Луны она равна MG/R2, а R(dф/dt)2 — это центробежное ускорение. Результат известен ar =0.
Где же вы оказались правы, когда всё ошибочно?
Вот тут я и оказался прав. Подменить центростремительную силу центробежной для демонстрации ложного результата не каждому дано.
PS. Результаты расчетов стационарного движения по кругу в вашей ссылке, скорее всего, правильные. В ней показано, чтобы такое движение было стационарным, необходимо иметь центростремительную силу равную центробежной. Хотя, выражение для радиального ускорения записано ошибочно. Правильная запись ar =R(dф/dt)2 + d2R/dt2. Центростремительная сила и ускорение должны быть направлены в сторону уменьшения радиуса. Вторая производная от R отрицательна. Поэтому, вопреки вашему упорному непониманию действия сил при круговом движении, радиальное ускорение равно нулю.
отредактировал(а) Fedor: 2025-03-20 11:19 GMT

#69043 Fedor :#69040 zam :#69036 Fedor :— ускорение радиальное: \(a_r=-R\dot{\varphi}^2\) ;
Формально так, но так как dф/dt=const, вторая производная по времени от нее равна нулю и следовательно радиальное ускорение равно нулю.
Результат невнимательного прочтения текста.
Ну так читайте внимательно. Кто вам мешает?
В выражение для радиального ускорения вторая производная от угла \(\varphi\) не входит. Для произвольного движения \(a_r=\ddot r — r \dot \varphi ^2\) , для равномерного движения по окружности \(a_r= — R \dot \varphi ^2\) .
Если вторая производная радиуса участвует в произвольном движении, то она должна участвовать и в равномерном движении по окружности.
Никакие производные ни в каком движении не участвуют. Производные участвуют в математическом описании движения.
При произвольном движении нармальное ускорение равно: \(a_r=\ddot{r}-r\dot{\varphi }^2\).
При равномерном движении по окружности \(\ddot{r}=0\), поэтому \(a_r=-r\dot{\varphi }^2\) .
Для случая Луны она равна MG/R2, а R(dф/dt)2 — это центробежное ускорение. Результат известен ar =0.
Где же вы оказались правы, когда всё ошибочно?
Вот тут я и оказался прав. Подменить центростремительную силу центробежной для демонстрации ложного результата не каждому дано.
Ничего такого я не делал. Опять врёте, как всегда.
PS. Результаты расчетов стационарного движения по кругу в вашей ссылке, скорее всего, правильные.
Что ещё раз подтверждает — вы всегда врёте.
Вот вам ещё ссылка (может, и у вас откроется) : https://eos.belovokyzgty.ru/pluginfile.php/13410/mod_resource/content/1/Теор.механика%20Уч.пос.%20для%20всех%20Хямяляйнен%202020.pdf .
Смотрите страницы 63 и 67, формулы (1.19) и (1.32).

#69056 zam :#69043 Fedor :#69040 zam :При произвольном движении нармальное ускорение равно: \(a_r=\ddot{r}-r\dot{\varphi }^2\).
При равномерном движении по окружности \(\ddot{r}=0\), поэтому \(a_r=-r\dot{\varphi }^2\) .
Придется провести небольшой образовательный ликбез девятикласснику, изучающему механику.
- Скорость – это пройденный объектом путь за единицу времени. Величину и направление скорости называют вектором скорости. Математически скорость можно выразить через производную от пройденного пути по времени V=dL/dt.
- Ускорение – изменение величины скорости в направлении вектора скорости за единицу времени –тоже вектор. Ускорение может иметь и другие направления, если изменения скорости вызваны изменением направления скорости, однако всегда направление вектора ускорения совпадает с направлением суммарной действующей на объект силы. Нас интересуют случаи, когда ускорение имеет одно радиальное направление. В таком случае оно выражает радиальное изменение скорости и, следовательно, дает вклад в движение объекта в радиальном направлении. Составляющую ускорения вдоль любой координаты, например радиальной, можно выразить в виде второй производной aR=d2R/dt2. В этом случае указанное выражение определяет движение, которое приводит к реальному смещению объекта в радиальном направлении
- 3. Нас интересует движение в условиях полярной системы координат, которую составляют радиальная R координата и угловая Ф координата.
Автор обсуждаемого текста утверждает, что при произвольном (значит в любом месте и направлении) движения радиальную составляющую ускорения можно выразить формулой:
ar=R¨−Rφ˙2. В этом выражении мы видим два члена, дающих вклад в радиальное ускорение, один из которых приведен выше в виде второй производной от радиуса по времени. Заметим, если движение объекта происходит в условиях действия центральной радиальной силы, то вклад этой силы в радиальное ускорение будет иметь отрицательный знак.
Второй член в выражении связан с угловым движением объекта и отражает изменение направления его прямолинейного движения. В отсутствие углового движения радиальное ускорение определяется членом со второй производной. В отсутствие центральной силы объект будет двигаться прямолинейно. Член с квадратом угловой скорости определяет инерционное сопротивление изменению направления скорости объекта. Таким образом, его действие направлено в противоположную сторону от центростремительного ускорения. В приведенном выше выражении записан с ложным знаком (-). В условиях стационарного движения по окружности инерционная (центробежная) сила полностью компенсирует действие силы центростремительной, обращая в ноль суммарное радиальное ускорение, которое реализуется выражением ar=R¨+Rφ˙2=0.
Вот вам ещё ссылка (может, и у вас откроется) : https://eos.belovokyzgty.ru/pluginfile.php/13410/mod_resource/content/1/Теор.механика%20Уч.пос.%20для%20всех%20Хямяляйнен%202020.pdf .
Смотрите страницы 63 и 67, формулы (1.19) и (1.32).
Мне не нужны Ваши ссылки, тем более, что в большинстве случаев они недоступны по причине окончания ru, которое Украина блокирует. Демонстрируйте собственный ум и соображения, если они есть, и показывайте своими словами, в чем я неправ. Любые бездоказательные утверждения в виде «вранье» я воспринимаю, как вашу неспособность понять написанное мною.
отредактировал(а) Fedor: 2025-03-22 10:48 GMT

#69056 zam :При произвольном движении нармальное ускорение равно: \(a_r=\ddot{r}-r\dot{\varphi }^2\).
При равномерном движении по окружности \(\ddot{r}=0\), поэтому \(a_r=-r\dot{\varphi }^2\) .
Уважаемые великие физики zam и Фёдор, Вы в этом вопросе никогда вдвоём не разберётесь без арбитра и бутылки, и всегда будете обвинять друг друга во лжи, обмане и в незнание. Спорить о чём-то вдвоём по поводу правды и неправды по какому-то вопросу, это бессмысленное занятие. А арбитр сыт, пьян и нос в табаке.
Лучше подумайте и ответьте на вопрос, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает?

#69059 Хуснулла Алсынбаев :Уважаемые великие физики zam и Фёдор, Вы в этом вопросе никогда вдвоём не разберётесь без арбитра и бутылки, и всегда будете обвинять друг друга во лжи, обмане и в незнание. Спорить о чём-то вдвоём по поводу правды и неправды по какому-то вопросу, это бессмысленное занятие. А арбитр сыт, пьян и нос в табаке.
Лучше подумайте и ответьте на вопрос, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает
Хуснулла, надеюсь бутылка у Вас есть, я приглашаю Вас быть арбитром. Осталось уговорить zam-a. ![]()
В качестве компенсации отвечаю на Ваш вопрос. В формуле ЗВТ r2 имеет смысл площади сферы, через которую распространяется сила. Для точности добавьте туда 4 Пи. При этом F означает удельную долю силы, приходящуюся на единицу поверхности сферы.

#69060 Fedor :Хуснулла, надеюсь бутылка у Вас есть, я приглашаю Вас быть арбитром. Осталось уговорить zam-a.

В качестве компенсации отвечаю на Ваш вопрос. В формуле ЗВТ r2 имеет смысл площади сферы, через которую распространяется сила. Для точности добавьте туда 4 Пи. При этом F означает удельную долю силы, приходящуюся на единицу поверхности сферы.
Уважаемый Фёдор, хорошо, что Вы знаете, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает? А вот многие физики об этом элементарного понятия не имеют, и даже никогда не задавались этим. Это очень смешно и грустно. Самое удивительное в этом, они физики.
А вот быть арбитром, не возьмусь, во-первых, у меня нет бутылки, во-вторых, zam , от рождения, просто, упёртый, мои доводы будут слабоваты, они его не пробьют. Если он сказал, что квадрат Малевича белый, то это значит, что он для него белый и никто не убедит его в том, что квадрат чёрный. Сизифов труд. С такими лучше не связываться и держаться подальше, ведь они убеждены, что всё знают.
отредактировал(а) Хуснулла Алсынбаев: 2025-03-23 08:05 GMT

#69061 Хуснулла Алсынбаев :#69060 Fedor :
Уважаемый Фёдор, хорошо, что Вы знаете, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает? А вот многие физики об этом элементарного понятия не имеют, и даже никогда не задавались этим. Это очень смешно и грустно. Самое удивительное в этом, они физики.
Физики это понимают. Для них это не вопрос.
А вот быть арбитром, не возьмусь, во-первых, у меня нет бутылки, во-вторых, zam , от рождения, просто, упёртый, мои доводы будут слабоваты, они его не пробьют. Если он сказал, что квадрат Малевича белый, то это значит, что он для него белый и никто не убедит его в том, что квадрат чёрный. Сизифов труд. такими лучше не связываться и держаться подальше, ведь они убеждены, что всё знают.
В этом Вы правы. Он, если понимает, что проигрывает, то покидает тему безвозвратно.

#69058 Fedor :#69056 zam :При произвольном движении нармальное ускорение равно: \(a_r=\ddot{r}-r\dot{\varphi }^2\).
При равномерном движении по окружности \(\ddot{r}=0\), поэтому \(a_r=-r\dot{\varphi }^2\) .
Придется провести небольшой образовательный ликбез девятикласснику, изучающему механику.
Решили вывалить очередную порцию вранья? Ну, давайте. Чтобы даже до Хуснулла Алсынбаев дошло.
- Скорость – это пройденный объектом путь за единицу времени. Величину и направление скорости называют вектором скорости. Математически скорость можно выразить через производную от пройденного пути по времени V=dL/dt.
Нет. Средняя скорость — это перемещение объекта (векторная величина!) за некоторый промежуток времени \(\vec v_{ср}=\frac{\Delta \vec r}{\Delta t}\) .
При \(\Delta t \to 0\) получается мгновенная скорость: \(\vec v=\frac{d \vec r}{d t}\) .
1. Ускорение – изменение величины скорости в направлении вектора скорости за единицу времени –тоже вектор.
Нет. Ускорение - это \(\vec a=\frac{d \vec v}{d t}\). И никакого "в направлении вектора скорости".
2. Ускорение может иметь и другие направления, если изменения скорости вызваны изменением направления скорости, однако всегда направление вектора ускорения совпадает с направлением суммарной действующей на объект силы.
Направление ускорения почти никогда не совпадает с направлением скорости. Потому что направление силы почти никогда не совпадает с направлением скорости.
Нас интересуют случаи, когда ускорение имеет одно радиальное направление.
Вас ничего не интересует. Если бы интересовало, то вы читали бы учебники и не занимались враньём.
В таком случае оно выражает радиальное изменение скорости и, следовательно, дает вклад в движение объекта в радиальном направлении.
Враньё. Вклад в движение в радиальном направлении даёт радиальная скорость, а не радиальное ускорение.
Составляющую ускорения вдоль любой координаты, например радиальной, можно выразить в виде второй производной aR=d2R/dt2.
Враньё. Радиальное ускорение — это проекция ускорения на радиальное направление, а не производная радиальной скорости по времени.
4. Нас интересует движение в условиях полярной системы координат, которую составляют радиальная R координата и угловая Ф координата.
Движение не зависит от того, каким способом мы его описываем. В декартовых, в полярных, — результат должен быть одним и тем же. Если нет, то описание ошибочно.
Автор обсуждаемого текста утверждает, что при произвольном (значит в любом месте и направлении) движения радиальную составляющую ускорения можно выразить формулой:
ar=R¨−Rφ˙2.
Не просто утверждает. Доказывает (выводит эту формулу).
В этом выражении мы видим два члена, дающих вклад в радиальное ускорение, один из которых приведен выше в виде второй производной от радиуса по времени. Заметим, если движение объекта происходит в условиях действия центральной радиальной силы, то вклад этой силы в радиальное ускорение будет иметь отрицательный знак.
Враньё. \(\ddot R <0\) только в том случае, если центр сил притягивает рассматриваемое тело. Если отталкивает, то \(\ddot R > 0\) .
Член с квадратом угловой скорости определяет инерционное сопротивление изменению направления скорости объекта.
Враньё. Нет никакого «инерциального сопротивления». Это отец Fedor из своего носа выковырял приняв 0.5 кагора для вдохновения.
Таким образом, его действие направлено в противоположную сторону от центростремительного ускорения.
Враньё. \(-R \dot \varphi \leqslant 0\) всегда. То есть, это слагаемое радиального ускорения направлено всегда к центру (если только не равно нулю), даже если центр сил отталкивает рассматриваемое тело.
В приведенном выше выражении записан с ложным знаком (-).
Враньё. Выведите формулу, потом сможете что-то рассказывать про знаки.
В условиях стационарного движения по окружности инерционная (центробежная) сила полностью компенсирует действие силы центростремительной, обращая в ноль суммарное радиальное ускорение, которое реализуется выражением ar=R¨+Rφ˙2=0.
Враньё.
Вот вам ещё ссылка (может, и у вас откроется) : https://eos.belovokyzgty.ru/pluginfile.php/13410/mod_resource/content/1/Теор.механика%20Уч.пос.%20для%20всех%20Хямяляйнен%202020.pdf .
Смотрите страницы 63 и 67, формулы (1.19) и (1.32).
Мне не нужны Ваши ссылки,
Естественно. А как же ещё? Как говорил один полковник — «Как ни странно, существуют другие мнения, кроме моего, единственно правильного, мнения». Вы же у нас не читатель, вы писатель.
тем более, что в большинстве случаев они недоступны по причине окончания ru, которое Украина блокирует.
Значит, придётся вставить картинку.
Демонстрируйте собственный ум и соображения, если они есть, и показывайте своими словами, в чем я неправ.
Обязательно продемонстрирую.
Любые бездоказательные утверждения в виде «вранье» я воспринимаю, как вашу неспособность понять написанное мною.
Мои указания на ваше враньё всегда доказательны. Ваше враньё всегда бездоказательно. Понять вами написанное может даже Хуснулла Алсынбаев. Если он немного почитает учебники и немного подумает, то поймёт: всё вами написанное — враньё.

#69103 zam :#69058 Fedor :
- Скорость – это пройденный объектом путь за единицу времени. Величину и направление скорости называют вектором скорости. Математически скорость можно выразить через производную от пройденного пути по времени V=dL/dt.
Нет. Средняя скорость — это перемещение объекта (векторная величина!) за некоторый промежуток времени \(\vec v_{ср}=\frac{\Delta \vec r}{\Delta t}\) .
При \(\Delta t \to 0\) получается мгновенная скорость: \(\vec v=\frac{d \vec r}{d t}\) .
Пустословная поправка. Лишь бы было что сказать после слова «нет».
1. Ускорение – изменение величины скорости в направлении вектора скорости за единицу времени –тоже вектор.
Нет. Ускорение - это \(\vec a=\frac{d \vec v}{d t}\). И никакого "в направлении вектора скорости".
Беспочвенное возражение при наличии пункта 2 в моем сообщении.
2. Ускорение может иметь и другие направления, если изменения скорости вызваны изменением направления скорости, однако всегда направление вектора ускорения совпадает с направлением суммарной действующей на объект силы.
Направление ускорения почти никогда не совпадает с направлением скорости. Потому что направление силы почти никогда не совпадает с направлением скорости.
Пустословное «почти».
Нас интересуют случаи, когда ускорение имеет одно радиальное направление.
Вас ничего не интересует. Если бы интересовало, то вы читали бы учебники и не занимались враньём.
Когда сказать больше нечего, как находка слово «вранье».
В таком случае оно выражает радиальное изменение скорости и, следовательно, дает вклад в движение объекта в радиальном направлении.
Враньё. Вклад в движение в радиальном направлении даёт радиальная скорость, а не радиальное ускорение.
Когда сказать больше нечего…
S=vRt – это да, а куда делось aR t2/2? Кто тут больше врет?
Составляющую ускорения вдоль любой координаты, например радиальной, можно выразить в виде второй производной aR=d2R/dt2.
Враньё. Радиальное ускорение — это проекция ускорения на радиальное направление, а не производная радиальной скорости по времени.
Как Вы ее не назовите, она все равно имеет такую запись aR=d2R/dt2.
Автор обсуждаемого текста утверждает, что при произвольном (значит в любом месте и направлении) движения радиальную составляющую ускорения можно выразить формулой:
ar=R¨−Rφ˙2.
Не просто утверждает. Доказывает (выводит эту формулу).
В этом выражении мы видим два члена, дающих вклад в радиальное ускорение, один из которых приведен выше в виде второй производной от радиуса по времени. Заметим, если движение объекта происходит в условиях действия центральной радиальной силы, то вклад этой силы в радиальное ускорение будет иметь отрицательный знак.
Враньё. \(\ddot R <0\) только в том случае, если центр сил притягивает рассматриваемое тело. Если отталкивает, то \(\ddot R > 0\) .
В таком случае Вы никогда не заставите тело двигаться по круговой траектории вокруг центра.
Член с квадратом угловой скорости определяет инерционное сопротивление изменению направления скорости объекта.
Враньё. Нет никакого «инерциального сопротивления». Это отец Fedor из своего носа выковырял приняв 0.5 кагора для вдохновения.
Таким образом, его действие направлено в противоположную сторону от центростремительного ускорения.
Враньё. \(-R \dot \varphi \leqslant 0\) всегда. То есть, это слагаемое радиального ускорения направлено всегда к центру (если только не равно нулю), даже если центр сил отталкивает рассматриваемое тело.
Чушь откровенная. Знак минус в приведенном Вами виде означает вращение тела в противоположном углу направлении. Слагаемое ускорения, связанное с угловой скоростью, всегда направлено в сторону роста радиуса.
В приведенном выше выражении записан с ложным знаком (-).
Враньё. Выведите формулу, потом сможете что-то рассказывать про знаки.
Продолжение безграмотной ахинеи.
Демонстрирую. Пусть тело движется по круговой траектории, закрепленное тросиком. В некоторый момент с координатами r и ф тросик обрывается. В момент обрыва тросика в радиальном направлении тело начнет двигаться по закону R=r+aцб(dt)2/2.
В угловом направлении его путь запишем так dL=rф·dt. При этом образуется прямоугольный треугольник с гипотенузой R, которую определим из формулыR2=r2+(dL)2. Далее квадраты радиуса двух формул сравниваем пренебрегая членом с (dt)4.
r2+raцб(dt)2=r2 + (rф·dt)2
И из этой формулы получаем
ацб = r(ф·)2.
Знак положительный, направлен в сторону возрастания радиуса.
В условиях стационарного движения по окружности инерционная (центробежная) сила полностью компенсирует действие силы центростремительной, обращая в ноль суммарное радиальное ускорение, которое реализуется выражением ar=R¨+Rφ˙2=0.
Враньё.
Центробежное ускорение не вранье, а результат того, что не смотря на тянущую тело к центру силу, тело упирается, отталкивается от центра и рвет тросик.
Значит, придётся вставить картинку.
Демонстрируйте собственный ум и соображения, если они есть, и показывайте своими словами, в чем я неправ.
Обязательно продемонстрирую.
Пока что демонстрируете неудачно.
отредактировал(а) Fedor: 2025-03-25 13:20 GMT

#69064 Fedor :#69061 Хуснулла Алсынбаев :#69060 Fedor :
Уважаемый Фёдор, хорошо, что Вы знаете, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает? А вот многие физики об этом элементарного понятия не имеют, и даже никогда не задавались этим. Это очень смешно и грустно. Самое удивительное в этом, они физики.
Физики это понимают. Для них это не вопрос.
Уважаемый Фёдор, тогда скажите как физик, вот эта формула ЗВТ ( F = G*m1*m2/R^2), правильная или нет? Она правильно отражает действительную силу взаимодействие двух тел или нет? zam считает, что эта формула правильная. Я, лично, считаю, что эта формула неправильная и не отражает действительное взаимодействие двух тел.

#69059 Хуснулла Алсынбаев :#69056 zam :При произвольном движении нармальное ускорение равно: \(a_r=\ddot{r}-r\dot{\varphi }^2\).
При равномерном движении по окружности \(\ddot{r}=0\), поэтому \(a_r=-r\dot{\varphi }^2\) .
Уважаемые великие физики zam и Фёдор, Вы в этом вопросе никогда вдвоём не разберётесь без арбитра и бутылки, и всегда будете обвинять друг друга во лжи, обмане и в незнание.
Вы что же, лишены богом таланта отличать правду от вранья?
Спорить о чём-то вдвоём по поводу правды и неправды по какому-то вопросу, это бессмысленное занятие. А арбитр сыт, пьян и нос в табаке.
А кто тут спорит? Я демонстрирую желающим читать, что отец Fedor врет в каждом своём сообщении. Делаю это аргументированно, со ссылками на надёжные источники. Это спором называться не может.
Лучше подумайте и ответьте на вопрос, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает?
Формула Пуассона — это вот что: . \(\Delta\varphi\left( \vec r \right)=-4\pi G\rho \left( \vec r \right)\) . Здесь \(\varphi\) — гравитационный потенциал, \(\rho\) — плотность вещества, \(\Delta\) — оператор Лапласа.
В формуле Ньютона \(F = G \frac {m_1m_2}{r^2}\) (он её не написал, он её рассказал словами) \(r^2\) в заменателе означает, что частицы-переносчики гравитационного взаимодействия (гравитоны) имеют массу ноль и зарад ноль. Как и у электромагнитного взаимодействия (фотоны).

#69060 Fedor :В формуле ЗВТ r2 имеет смысл площади сферы, через которую распространяется сила.
Сила распространяться не может. Почитайте в учебнике, что такое сила.
А почему силы межатомного/межмолекулярного взаимодействия (силы Ван-дер-Ваальса) не подчиняются закону обратных квадратов? У них что, сферы другие?

#69061 Хуснулла Алсынбаев :Уважаемый Фёдор, хорошо, что Вы знаете, откуда, как и каким образом в формуле ЗВТ Пуассона ( F = G*m1*m2 / r^2) в знаменателе появилась ( r^2 ) и что она означает?
Он не знает.
А вот многие физики об этом элементарного понятия не имеют, и даже никогда не задавались этим.
А физики знают.
Это очень смешно и грустно. Самое удивительное в этом, они физики.
Самое удивительное, что вы пытаетесь оценивать физиков не имея ни малейшего понятия о физике.
А вот быть арбитром, не возьмусь, во-первых, у меня нет бутылки,
Это не проблема, можете купить. У вас нет другого, чего купить нельзя.
во-вторых, zam , от рождения, просто, упёртый
Да. У меня от рождения талант — отличать правду от вранья.
, мои доводы будут слабоваты, они его не пробьют.
А почему ваши доводы слабоваты?
Если он сказал, что квадрат Малевича белый, то это значит, что он для него белый и никто не убедит его в том, что квадрат чёрный.
Вот только я этого никогда не скажу. Зато я скажу, что квадрат Малевича не квадратный (и это правда!).
С такими лучше не связываться и держаться подальше, ведь они убеждены, что всё знают.
Вот тут вы ошибаетесь. Я знаю пренебрежимо мало. А про вас очень хорошо сказал Сократ: «Я знаю, что ничего не знаю, но многие не знают даже этого».

#69128 zam :Формула Пуассона — это вот что: . \(\Delta\varphi\left( \vec r \right)=-4\pi G\rho \left( \vec r \right)\) . Здесь \(\varphi\) — гравитационный потенциал, \(\rho\) — плотность вещества, \(\Delta\) — оператор Лапласа.
В формуле Ньютона \(F = G \frac {m_1m_2}{r^2}\) (он её не написал, он её рассказал словами) \(r^2\) в заменателе означает, что частицы-переносчики гравитационного взаимодействия (гравитоны) имеют массу ноль и зарад ноль. Как и у электромагнитного взаимодействия (фотоны).
Почему-то я был уверен, что zam знает, кто придумал и написал формулу закона всемирного тяготения (F = G*m1*m2/R^2), откуда в нём появилась R^2и что она означает? Но я ошибся, а жаль. Я-то думал, что он первейший физик в здешней округе. Вот что пишет zam «»»» В формуле Ньютона F=Gm1m2r2 (он её не написал, он её рассказал словами) r2 в заменателе означает, что частицы-переносчики гравитационного взаимодействия (гравитоны) имеют массу ноль и заряд ноль. Как и у электромагнитного взаимодействия (фотоны). «»»»». Это же надо! Никто не видел и не поймал ни одного гравитона и тем более не обучил, а он уже рулит ими и ездит на них, как на фотоне. Это, полнейшее незнание предмета. Придётся мне взяться за него, объяснять всё подробно и вводить в курс. Только вот, есть одна проблема, он будет игнорировать мои объяснения, а хуже всего, он будет удалять мои посты под предлогом, что я врач, врун и вру, или вообще удалит всю тему к чёртовой матери в унитаз, что случалось уже не раз. И пропадут все мои потуги со слезами на глазах. Он на всё способен, он же главный модератор из главных, и все пава у него в кармане. Но вот, если он гарантированно пообещает не пользоваться своими правами и не хулиганить, то я ему выложу всю правду в глаза, как на духу, что я об этой проблеме думаю.

#69116 Хуснулла Алсынбаев :Уважаемый Фёдор, тогда скажите как физик,
Ну какой же он физик? Окончить физфак (или физтех?) ХГУ — это не значит быть физиком.
вот эта формула ЗВТ ( F = G*m1*m2/R^2), правильная или нет? Она правильно отражает действительную силу взаимодействие двух тел или нет?
Правильная. Подтверждена экпериментально.
zam считает, что эта формула правильная.
zam знает, что эта формула приблизительная (подходит для не очень больших масс, не очень больших скоростей). Более точная формула в общей теории относительности.
Кроме того, следует помнить, что это формула для взаимодействия двух точечных масс. Для тел произвольной формы гораздо лучше формула Пуассона.
Я, лично, считаю, что эта формула неправильная и не отражает действительное взаимодействие двух тел.
Чтобы лично считать, нужно, перво-наперво, научиться считать.
Для начала, решите кеплерову задачу для пары «Земля-Луна».

#69129 zam :#69060 Fedor :В формуле ЗВТ r2 имеет смысл площади сферы, через которую распространяется сила.
Сила распространяться не может. Почитайте в учебнике, что такое сила.
Правила цивилизованного общения рекомендуют отвечать на вопросы собеседника на понятном ему языке. Мой ответ Хуснулле оказался ему понятным.
Если бы я отвечал на такой же вопрос физика, то ответил бы примерно так: В формуле ЗВТ r2имеет смысл площади сферы, через которую распространяется полный поток вектора напряженности гравитационного поля.
Вам мне сложно ответить понятно. С одной стороны Вы кичитесь своими знаниями и образованностью, а с другой стороны не понимаете реального содержания центробежного ускорения, не понимаете в какой системе координат написано уравнение движения тела по круговой орбите. Да и самое простое обыкновенное диф-уравнение не можете правильно анализировать.
А почему силы межатомного/межмолекулярного взаимодействия (силы Ван-дер-Ваальса) не подчиняются закону обратных квадратов? У них что, сферы другие?
На этот вопрос ответить не могу. В силах Ван-дер-Ваальса я не копенгаген.

#69058 Fedor :
в большинстве случаев они недоступны по причине окончания ru, которое Украина блокирует.
#69103 zam :Значит, придётся вставить картинку.
Выполняю обещание.
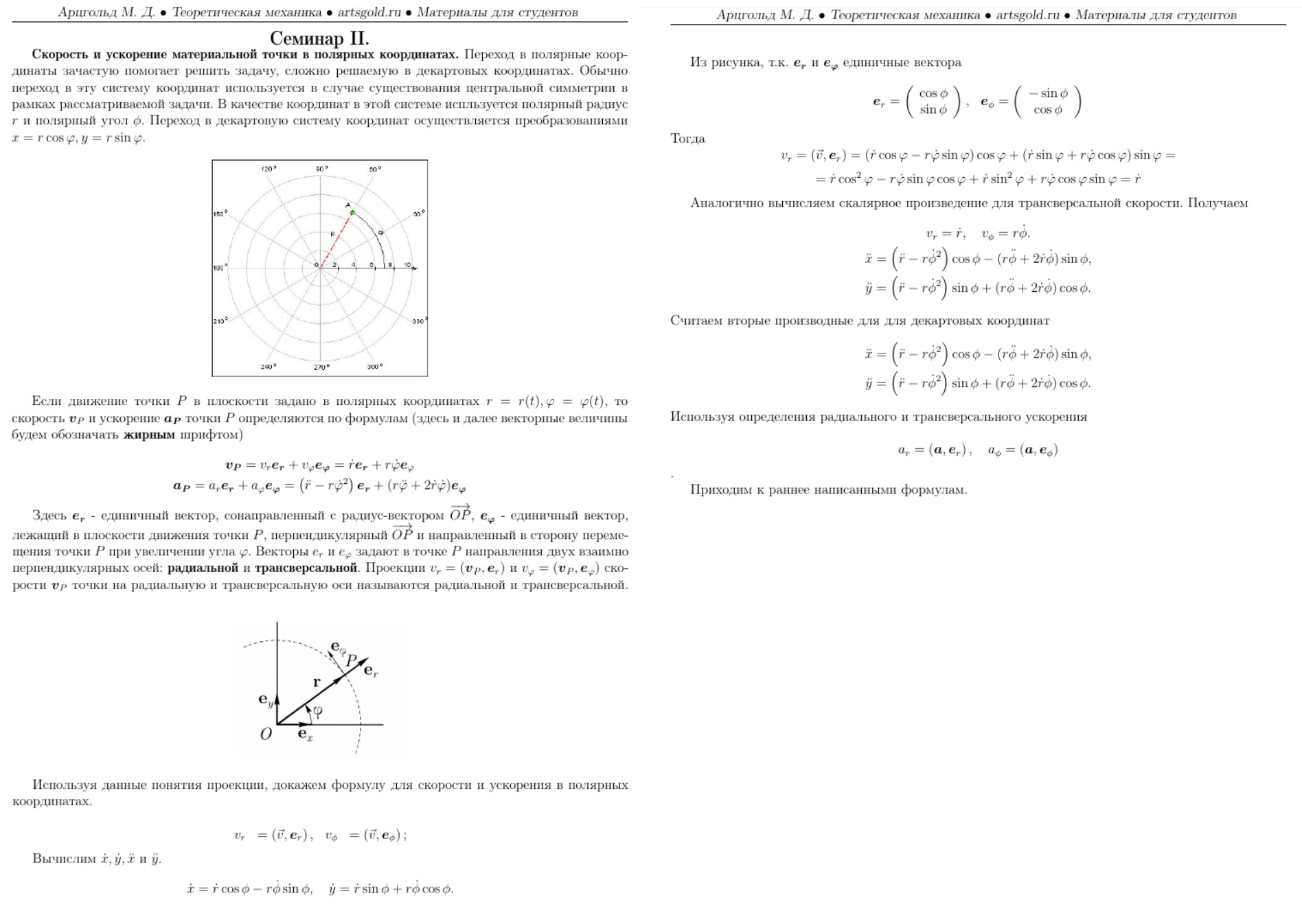
Отец Fedor! Теперь у вас только два пути:
1) либо вы находите ошибку в предложенном выводе формул для радиального и тангенциального ускорений;
2) либо признаёте, что всё вами написанное по этому поводу представляет собой ахинею.
А пока вы этого не сделпете («1» или «2») объявляется мораторий на публикацию сообщений отца Fedor'а на форуме. То есть, все его сообщения, не относящиеся к пунктам «1» или «2», будут удаляться.

#69064 Fedor :#69061 Хуснулла Алсынбаев :откуда, как и каким образом в формуле ЗВТ в знаменателе появилась ( r^2 ) и что она означает?
Физики это понимают. Для них это не вопрос.
Физики это понимают. Отец Fedor — нет.
Он [zam], если понимает, что проигрывает, то покидает тему безвозвратно.
Очередное враньё от отца Fedor'а.

#69111 Fedor :#69103 zam :#69058 Fedor :
- Скорость – это пройденный объектом путь за единицу времени. Величину и направление скорости называют вектором скорости. Математически скорость можно выразить через производную от пройденного пути по времени V=dL/dt.
Нет. Средняя скорость — это перемещение объекта (векторная величина!) за некоторый промежуток времени \(\vec v_{ср}=\frac{\Delta \vec r}{\Delta t}\) .
При \(\Delta t \to 0\) получается мгновенная скорость: \(\vec v=\frac{d \vec r}{d t}\) .
Пустословная поправка. Лишь бы было что сказать после слова «нет».
Какая же она пустословная, если показывает, что вы в очередной раз соврали?
1. Ускорение – изменение величины скорости в направлении вектора скорости за единицу времени –тоже вектор.
Нет. Ускорение - это \(\vec a=\frac{d \vec v}{d t}\). И никакого "в направлении вектора скорости".
Беспочвенное возражение при наличии пункта 2 в моем сообщении.
Возражение — по существу. Потому что никакое утверждение не может базироваться на чуши.
2. Ускорение может иметь и другие направления, если изменения скорости вызваны изменением направления скорости, однако всегда направление вектора ускорения совпадает с направлением суммарной действующей на объект силы.
Направление ускорения почти никогда не совпадает с направлением скорости. Потому что направление силы почти никогда не совпадает с направлением скорости.
Пустословное «почти».
А вы не согласны, что это «пустословное» слово является правильным. А ваше многословное (и поэтому действительно пустословное) сообщение является просто пересказом второго закона Ньютона, который записывается четырьмя символами \(\vec F=m \vec a\) ?
Нас интересуют случаи, когда ускорение имеет одно радиальное направление.
Вас ничего не интересует. Если бы интересовало, то вы читали бы учебники и не занимались враньём.
Когда сказать больше нечего, как находка слово «вранье».
Вы хотите возразить, что на самом деле читаете учебники???
В таком случае оно выражает радиальное изменение скорости и, следовательно, дает вклад в движение объекта в радиальном направлении.
Враньё. Вклад в движение в радиальном направлении даёт радиальная скорость, а не радиальное ускорение.
Когда сказать больше нечего…
Вы и с этим утверждением не согласны?
S=vRt – это да, а куда делосьКто тут больше врет?
А откуда взялось aR t2/2? Как всегда, врёте вы и только вы.
Составляющую ускорения вдоль любой координаты, например радиальной, можно выразить в виде второй производной aR=d2R/dt2.
Враньё. Радиальное ускорение — это проекция ускорения на радиальное направление, а не производная радиальной скорости по времени.
Как Вы ее не назовите, она все равно имеет такую запись aR=d2R/dt2.
Нет. Попробуйте это доказать.
Автор обсуждаемого текста утверждает, что при произвольном (значит в любом месте и направлении) движения радиальную составляющую ускорения можно выразить формулой:
ar=R¨−Rφ˙2.
Не просто утверждает. Доказывает (выводит эту формулу).
В этом выражении мы видим два члена, дающих вклад в радиальное ускорение, один из которых приведен выше в виде второй производной от радиуса по времени. Заметим, если движение объекта происходит в условиях действия центральной радиальной силы, то вклад этой силы в радиальное ускорение будет иметь отрицательный знак.
Враньё. \(\ddot R <0\) только в том случае, если центр сил притягивает рассматриваемое тело. Если отталкивает, то \(\ddot R > 0\) .
В таком случае Вы никогда не заставите тело двигаться по круговой траектории вокруг центра.
Докажите. Или признайте, что опять соврали.
Член с квадратом угловой скорости определяет инерционное сопротивление изменению направления скорости объекта.
Враньё. Нет никакого «инерциального сопротивления». Это отец Fedor из своего носа выковырял приняв 0.5 кагора для вдохновения.
Таким образом, его действие направлено в противоположную сторону от центростремительного ускорения.
Враньё. \(-R \dot \varphi \leqslant 0\) всегда. То есть, это слагаемое радиального ускорения направлено всегда к центру (если только не равно нулю), даже если центр сил отталкивает рассматриваемое тело.
Чушь откровенная. Знак минус в приведенном Вами виде означает вращение тела в противоположном углу направлении. Слагаемое ускорения, связанное с угловой скоростью, всегда направлено в сторону роста радиуса.
Там опечатка. Следует читать \(-R \dot \varphi ^2 \leqslant 0\) . Что хорошо видно из написанных ранее формул (могли бы и сами догадаться). И это выражение выполняется всегда, при любом направлении вращения.
В приведенном выше выражении записан с ложным знаком (-).
Враньё. Выведите формулу, потом сможете что-то рассказывать про знаки.
Продолжение безграмотной ахинеи.
Это верно. Ваша ахинея, видимо, неостановима. Но я попробую. Объявил мораторий на ахинею.
Демонстрирую. Пусть тело движется по круговой траектории, закрепленное тросиком. В некоторый момент с координатами r и ф тросик обрывается. В момент обрыва тросика в радиальном направлении тело начнет двигаться по закону R=r+aцб(dt)2/2.
Враньё. После обрыва тросика тело движется прямолинейно. Уравнение этой прямой линии в полярных координатах \(R\left( t \right)=\sqrt{R_0^2+v_0^2t^2}; \;\; \varphi \left( t \right)=arctg\frac{vt}{R_0}\) .
В угловом направлении его путь запишем так dL=rф·dt. При этом образуется прямоугольный треугольник с гипотенузой R, которую определим из формулыR2=r2+(dL)2. Далее квадраты радиуса двух формул сравниваем пренебрегая членом с (dt)4.
r2+raцб(dt)2=r2 + (rф·dt)2
И из этой формулы получаем
ацб = r(ф·)2.
Знак положительный, направлен в сторону возрастания радиуса.
Полный бред. Послушайте, как вам удалось окончить физфак (или техфак) ХГУ? Или и тут вы соврали?
В условиях стационарного движения по окружности инерционная (центробежная) сила полностью компенсирует действие силы центростремительной, обращая в ноль суммарное радиальное ускорение, которое реализуется выражением ar=R¨+Rφ˙2=0.
Враньё.
Центробежное ускорение не вранье, а результат того, что не смотря на тянущую тело к центру силу, тело упирается, отталкивается от центра и рвет тросик.
Центробежное ускорение — не враньё. Но вы понятия не имеете, что это такое, и поэтому про него врёте.
Значит, придётся вставить картинку.
Демонстрируйте собственный ум и соображения, если они есть, и показывайте своими словами, в чем я неправ.
Обязательно продемонстрирую.
Пока что демонстрируете неудачно.
Пока что вы не обнаружили у меня ни одной ошибки, при этом публикуя ахинею непрерывно.

#69132 Хуснулла Алсынбаев :#69128 zam :Формула Пуассона — это вот что: . \(\Delta\varphi\left( \vec r \right)=-4\pi G\rho \left( \vec r \right)\) . Здесь \(\varphi\) — гравитационный потенциал, \(\rho\) — плотность вещества, \(\Delta\) — оператор Лапласа.
В формуле Ньютона \(F = G \frac {m_1m_2}{r^2}\) (он её не написал, он её рассказал словами) \(r^2\) в заменателе означает, что частицы-переносчики гравитационного взаимодействия (гравитоны) имеют массу ноль и зарад ноль. Как и у электромагнитного взаимодействия (фотоны).
Почему-то я был уверен, что zam знает, кто придумал и написал формулу закона всемирного тяготения (F = G*m1*m2/R^2), откуда в нём появилась R^2и что она означает? Но я ошибся, а жаль.
Разве я не ответил на ваши вопросы? Они противоречат тому, что вы себе навыдумывали и поэтому вам не нравятся? А я тут при чём?
Немного могу уточнить. Вот труд Ньютона: https://djvu.online/file/wCBIlGHJY68zQ https://djvu.online/file/wCBIlGHJY68zQ. На странице 92 написано:
«Следовательно, центростремительная сила обратно пропорциональна квадрату расстояния SP [квадрату расстояния от тела до фокуса эллипса]»
Это и есть r2 в знаменателе. Собственно, про это говорили и до Ньютона (он упоминает трёх предшественников — Булиальд, Рен, Гук). Но они это предполагали, а Ньютон доказал.
Я-то думал, что он первейший физик в здешней округе.
Я не физик.
Вот что пишет zam «»»» В формуле Ньютона F=Gm1m2r2 (он её не написал, он её рассказал словами) r2 в заменателе означает, что частицы-переносчики гравитационного взаимодействия (гравитоны) имеют массу ноль и заряд ноль. Как и у электромагнитного взаимодействия (фотоны). «»»»». Это же надо!
И что вам тут не нравится?
Никто не видел и не поймал ни одного гравитона и тем более не обучил, а он уже рулит ими и ездит на них, как на фотоне.
Тем не менее, основные свойства гравитонов уже известны. А вот чего я не знал, так это того, ято гравитоны нуждаются в обучении.
Это, полнейшее незнание предмета.
Это знание основ предмета.
Придётся мне взяться за него, объяснять всё подробно и вводить в курс.
Чтобы что-то объяснять, нужно самому что-то понимать. А у вас с этим очень большие проблемы.
Только вот, есть одна проблема, он будет игнорировать мои объяснения,
Если объяснения будут толковыми, то зачем же игнорировать? Вот только объяснения не должны противоречить известным факта. Вы обещаете?
а хуже всего, он будет удалять мои посты под предлогом, что я врач, врун и вру, или вообще удалит всю тему к чёртовой матери в унитаз, что случалось уже не раз.
Ни разу не удалял ни ваших сообщений, ни ваших тем. Даже ни одного предупреждения вам не вынес. Если сообщение не нарушает правил форума (вы их читали?), то я его не удаляю.
Он на всё способен, он же главный модератор из главных, и все пава у него в кармане.
Нет, не главный. И прав у меня очень мало. Я, например, не могу забанить пользователя (а некоторые заслуживают).
Но вот, если он гарантированно пообещает не пользоваться своими правами и не хулиганить, то я ему выложу всю правду в глаза, как на духу, что я об этой проблеме думаю.
Давайте! Вот только сомневаюсь, что вам известна правда.

#69143 Fedor :#69129 zam :#69060 Fedor :В формуле ЗВТ r2 имеет смысл площади сферы, через которую распространяется сила.
Сила распространяться не может. Почитайте в учебнике, что такое сила.
Правила цивилизованного общения рекомендуют отвечать на вопросы собеседника на понятном ему языке.
Правила цивилизованного общения обязывают отвечать на вопросы собеседника без вранья.
Мой ответ Хуснулле оказался ему понятным.
Но он представляет собой враньё.
Если бы я отвечал на такой же вопрос физика, то ответил бы примерно так: В формуле ЗВТ r2имеет смысл площади сферы, через которую распространяется полный поток вектора напряженности гравитационного поля.
Ну да. Это теорема Гаусса. А физик спросил бы — а почему полный поток вектора напряженности гравитационного поля одинаков через сферу любого радиуса?
Вам мне сложно ответить понятно.
Это не важно. Попробуйте ответить правильно. Или принцип «Враньё, только враньё, ничего, кроме вранья» вам этого сделать не позволяет?
С одной стороны Вы кичитесь своими знаниями и образованностью,
Моей образованности только и хватает на то, чтобы отличать правду от вранья.
а с другой стороны не понимаете реального содержания центробежного ускорения, не понимаете в какой системе координат написано уравнение движения тела по круговой орбите.
Чего же тут понимать? Ежу понятно — всё вами написанное на эту тему — сплошное враньё.
Да и самое простое обыкновенное диф-уравнение не можете правильно анализировать.
Опять враньё. Могу.
А почему силы межатомного/межмолекулярного взаимодействия (силы Ван-дер-Ваальса) не подчиняются закону обратных квадратов? У них что, сферы другие?
На этот вопрос ответить не могу. В силах Ван-дер-Ваальса я не копенгаген.
Ой! Чудо!!! Отец Fedor первый раз не соврал.
А ответ элементарен. Потому что частицы-переносчики этого взаимодействия (электроны) имеют ненулевую массу и ненулевой заряд.
Вот как выглядит зависимость силы межатомного взаимодействия от расстояния между атомами (левая картинка):


#69145 zam :Отец Fedor! Теперь у вас только два пути:
1) либо вы находите ошибку в предложенном выводе формул для радиального и тангенциального ускорений;
2) либо признаёте, что всё вами написанное по этому поводу представляет собой ахинею.
Вы не предложили вывода формул радиального и тангенциального ускорений. Выражения для ускорений Вами представлены в готовом виде без вывода. Подскажите, как найти ошибку в выводе, которого нет?

Комментарий от zam.
Там же написано: «докажем формулу для скорости и ускорения в полярных координатах». И на следующей странице доказательство, весьма короткое.
Дальнейшие глупости удалены. Причина: мораторий.
отредактировал(а) zam: 2025-03-27 00:05 GMT

deleted
Причина: мораторий.
отредактировал(а) zam: 2025-03-27 00:07 GMT

от zam:
Там же написано: «докажем формулу для скорости и ускорения в полярных координатах». И на следующей странице доказательство, весьма короткое.
Там приведен вывод только для радиальной скорости vR=r· и дважды выложены выражения для вторых производных декартовых координат, выраженные через полярные координаты.
Комментарий от zam.
А выражения для трёх других величин - скорости трансверсальной \(v_{ \varphi}\) , ускорения радиального \(a_r\), ускорения трансверсального \(a_{ \varphi}\) — выводятся аналогично (предлагается студентам самостоятельно потренироваться).
Показываю, как это делается для радиального ускорения.
\(a_r=\left( \vec a, \vec e_r\right)=\ddot x cos\varphi + \ddot y sin\varphi= \\=\left[ \left( \ddot r — r \dot \varphi \right)cos \varphi-\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) sin \varphi\right]cos\varphi+\left[ \left( \ddot r — r \dot \varphi \right)sin \varphi+\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) cos \varphi\right]sin\varphi= \ddot r -r \dot\varphi ^2\)
Остальное сделайте самостоятельно.
Мораторий продолжается.
отредактировал(а) zam: 2025-03-27 10:13 GMT

#69155 Fedor :Показываю, как это делается для радиального ускорения.
\(a_r=\left( \vec a, \vec e_r\right)=\ddot x cos\varphi + \ddot y sin\varphi= \\=\left[ \left( \ddot r — r \dot \varphi \right)cos \varphi-\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) sin \varphi\right]cos\varphi+\left[ \left( \ddot r — r \dot \varphi \right)sin \varphi+\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) cos \varphi\right]sin\varphi= \ddot r -r \dot\varphi ^2\)
Остальное сделайте самостоятельно.
Фёдор, нет бы чтоб сразу так вывод оформить, давно был бы конец пустой перепалке. И охото было Вам языком чесать?
Уважаемый Фёдор, в чём логика, что ускорение тела умножают на пройденное им расстояние (a * S) и что получается в результате? Я это действо никогда не понимал и не понимаю до сих пор.
отредактировал(а) Хуснулла Алсынбаев: 2025-03-27 16:37 GMT

#69165 Хуснулла Алсынбаев :#69155 Fedor :Комментарий от zam.Показываю, как это делается для радиального ускорения.
\(a_r=\left( \vec a, \vec e_r\right)=\ddot x cos\varphi + \ddot y sin\varphi= \\=\left[ \left( \ddot r — r \dot \varphi \right)cos \varphi-\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) sin \varphi\right]cos\varphi+\left[ \left( \ddot r — r \dot \varphi \right)sin \varphi+\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) cos \varphi\right]sin\varphi= \ddot r -r \dot\varphi ^2\)
Остальное сделайте самостоятельно.
Фёдор, нет бы чтоб сразу так вывод оформить, давно был бы конец пустой перепалке. И охото было Вам языком чесать?
Вот только сделал это не Fedor (он так не умеет, он умеет только врать).

#69166 zam :#69165 Хуснулла Алсынбаев :#69155 Fedor :Комментарий от zam.Показываю, как это делается для радиального ускорения.
\(a_r=\left( \vec a, \vec e_r\right)=\ddot x cos\varphi + \ddot y sin\varphi= \\=\left[ \left( \ddot r — r \dot \varphi \right)cos \varphi-\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) sin \varphi\right]cos\varphi+\left[ \left( \ddot r — r \dot \varphi \right)sin \varphi+\left( r \ddot \varphi + 2 \dot r \dot \varphi \right) cos \varphi\right]sin\varphi= \ddot r -r \dot\varphi ^2\)
Остальное сделайте самостоятельно.
Фёдор, нет бы чтоб сразу так вывод оформить, давно был бы конец пустой перепалке. И охото было Вам языком чесать?
Вот только сделал это не Fedor (он так не умеет, он умеет только врать).
Да ладно, будет Вам. Ну и что, что наврал? Ну и что из этого, Ваша физика что ли перевернулась на изнану? Поболтали и забыли. Врать тоже надо уметь. Без врань не интересно, Почитайте художественную литературу, там одно враньё, что выдумал и нафонтнизировал автор лёжа на диване. Чем круче нафантазировал, тем интереснее читателю. Слава врачам, то биш. врунам"





