Решение задачи по физике по механике



Упадет весь рой.

Задача дурацкая. Составлена дураком. Не имеет решения.
Относительная скорость Земли и кометы никогда не может быть равной 3 км в сек.Скорость комет у земли от 16 км в сек и выше, до 30 км /сек и более. Поэтому они очень опасны.
Они сводят ее к геометрии.
Нарисуйте шарик Земли и тракторию роя. Какую то часть плошади заимет земля к рою во времени.
Отсюда решение.Так нельзя делать.В рое могут быть разного размера осколки, обломки, куски кометы.
Это показано в фильме Армагеддон.
Cкорость Тунгусского метеорита относительно земли 27 kм/с!!!
отредактировал(а) marsdmitri: 2025-02-05 01:52 GMT

#68032 marsdmitri :Задача дурацкая. Составлена дураком.
Сообщение дурацкое. Отправлено на форум дураком.
Не имеет решения.
Имеет.

#67946 Maxxis06 :

учловие задачи не полное. Не указано, как направлена скорость клметы относительно Земли (в системе отсчёта Земли). Подразумевается, что точно на Землю. Но это следовало написать в условии.
Вот иллюстрация:
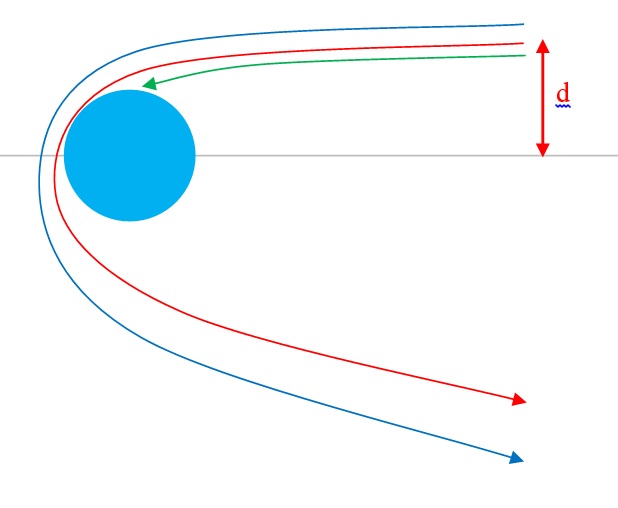
На Землю попадут те части роя, для которых прицельный параметр d меньше некоторого критического значения. Решение задачи сводится к определению критического значения этого параметра (ему соответствует параболлическая траектория, на рисунке она красная).

Все траектории частиц роя — гиперболические без исключения. Критическое значение прицельного параметра \(a_{кр}=R\sqrt{\displaystyle \frac{v_2^2}{v_\infty^2}+1}=6400\sqrt{\displaystyle \frac{11{,}2^2}{2{,}8^2}+1}=26400\) км, где \(v_2=11{,}2\) км/с — вторая космическая скорость. Так как радиус роя 25000 км, то упадет весь рой.

Общий ответ в задаче в зависимости от параметров следующий. Если диаметр роя \(d\) таков, что \(d\le 2a_{кр}\), где \(a_{кр}=R\sqrt{\displaystyle \frac{v_2^2}{v_\infty^2}+1}\), то доля роя, упавшего на Землю — единица (\(k=1\), весь рой упадет). В противном случае \(\displaystyle k=1-\left(1-\frac{4a_{кр}^2}{d^2}\right)^{3/2}\). Предполагалось, что рой шаровый однородный, и центр Земли пролетает через центр роя.
Для иллюстрации привожу график зависимости доли \(k\) от скорости кометы \(v_\infty\) при фиксированном \(d=50000\) км:


#68047 drobyshev :\(v_2=11{,}2\) км/с — вторая космическая скорость.
Это вторая космическая скорость на поверхности Земли.
Для других расстояний \(v_2=\sqrt{\frac{2GM_З}{R}}\) .
А вывод приведённой вами формулы можете привести?
Моё решение.
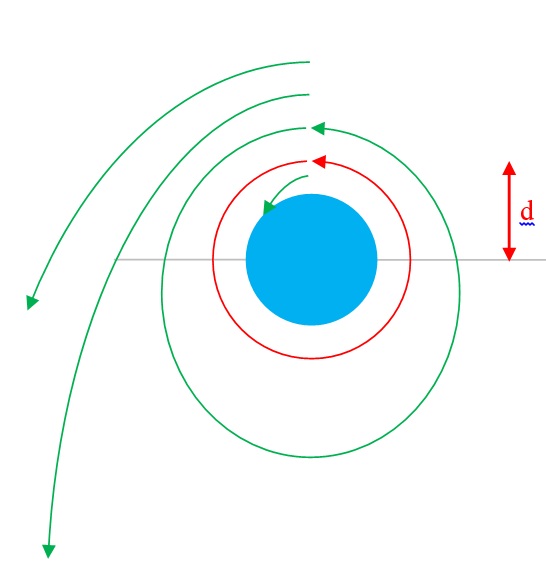
Тело, двигающееся со скоростью v = 2.8 км/с = 2800 м/с на расстоянии d от центра Земли может двигаться по окружности, эллипсу, параболе и гиперболе.
Чтобы двигаться по окружности скорость тела должна равняться \(v_1=\sqrt{\frac{GM_З}{R}}\) (первая космическая скорость), красная траектория на рисунке. Упадут на Землю тела, скорость которых меньше первой космической
\(v<v_1\) .
Отсюда
\(d<\frac{GM_З}{v_1^2}=\frac{\left(6.67 \cdot 10^{-11} \frac{Н \cdot м^2}{кг^2} \right)\left( 6 \cdot 10^{24} \; кг \right)}{\left(2800\frac{м}{с} \right)^2}=5.1\cdot 10^7 \; м=51000 \; км\) .
Так как радиус роя (25000 км) меньше d, весь рой упадёт на Землю. Все траектории эллиптические.
отредактировал(а) zam: 2025-01-14 14:54 GMT

#68066 zam :Все траектории эллиптические.
Нет, в системе отсчета Земли все траектории гиперболические. В этой системе на большом расстоянии от Земли все частицы роя имеют одну и ту же скорость \(v_\infty\) (она задана в условии). Частица приближается к Земле по ветви гиперболы. Далее, если она не сталкивается с Землей, то ее максимальная скорость \(v_p>v_\infty\) достигается в перигее на расстоянии \(r_p\) от центра Земли. Пролетев перигей, частица уходит от Земли по второй ветви гиперболы. На большом удалении от Земли ее скорость снова становится равной \(v_\infty\).
#68066 zam :.А вывод приведённой вами формулы можете привести?
Пусть прицельный параметр частицы \(a\) (изначально не совсем удачно обозначил, обычно обозначают \(b\), ну да ладно). Не теряя общности, ее массу считаем единичной. Модуль момента импульса частицы — это произведение ее скорости на расстояние прямой вдоль вектора скорости до центра Земли. Записываем законы сохранения момента импульса и энергии для двух положений — на большом удалении и в перигее:
\(\displaystyle v_\infty a=v_p r_p, \qquad \frac{1}{2}v_\infty^2=\frac{1}{2}v_p^2-\frac{GM}{r_p}.\)
Исключаем из уравнений \(v_p\) и получаем \(\displaystyle a=r_p\sqrt{\frac{2GM}{v_\infty^2 r_p}+1}.\) Очевидно, что функция \(a=a(r_p)\) — возрастающая.
Теперь важный момент. Частица падает на Землю, если ее перигей \(r_p\) оказывается меньше радиуса Земли \(R\). Это означает, что должно быть \(a<a_{кр}\), где критическое значение прицельного параметра находится из условия \(r_p=R\), т.е. \(\displaystyle a_{кр}=R\sqrt{\frac{2GM}{v_\infty^2 R}+1}\). Но \(\displaystyle v_2=\sqrt{\frac{2GM}{R}}\) — это вторая космическая скорость. Окончательно, \(\displaystyle a_{кр}=R\sqrt{\frac{v_2^2}{v_\infty^2}+1}\). Подставляя сюда \(v_\infty=2{,}8\) км/с, получаем \(a_{кр}=26400\) км. Все прицельные расстояния меньше чем \(d/2=25000\) км, поэтому весь рой упадет на Землю.

Интуитивно понятны предельные случаи формулы \(\displaystyle a_{кр}=R\sqrt{\frac{v_2^2}{v_\infty^2}+1}\) . Если \(v_\infty \to 0\), то \(a_{кр} \to \infty\). Это значит, что при малых скоростях частиц роя все они захватываются гравитацией Земли и падают на нее. Если же \(v_\infty \to \infty\), то \(a_{кр} \to R\), т.е. при больших скоростях частиц роя гравитация слабо влияет на форму траекторий — они практически прямые, и на Землю падают те частицы роя, которые участвуют в лобовых столкновениях.

#68068 drobyshev :#68066 zam :Все траектории эллиптические.
Нет, в системе отсчета Земли все траектории гиперболические. В этой системе на большом расстоянии от Земли все частицы роя имеют одну и ту же скорость \(v_\infty\) (она задана в условии).
В условии задана скорость 2.8 км/с в непосредственной близости от Земли, никак не на бесконечности. Если бы это была скорость вдалеке от Земли, то мы ничего не могли бы сказать про скорость рядом с Землёй. Кометы в Солнечной системе не летают по прямым линиям и с постоянными скоростями. К тому же, если комета летит к Солнцу, то её скорость увеличивается, а если от Солнца, то уменьшается.
Частица приближается к Земле по ветви гиперболы.
Мы ничего не можем знать о траектории частиц вдалеке от Земли — данных недостаточно.
#68066 zam :.А вывод приведённой вами формулы можете привести?
Пусть прицельный параметр частицы \(a\) (изначально не совсем удачно обозначил, обычно обозначают \(b\), ну да ладно). Не теряя общности, ее массу считаем единичной. Модуль момента импульса частицы — это произведение ее скорости на расстояние прямой вдоль вектора скорости до центра Земли. Записываем законы сохранения момента импульса и энергии для двух положений — на большом удалении и в перигее:
\(\displaystyle v_\infty a=v_p r_p, \qquad \frac{1}{2}v_\infty^2=\frac{1}{2}v_p^2-\frac{GM}{r_p}.\)
Исключаем из уравнений \(v_p\) и получаем \(\displaystyle a=r_p\sqrt{\frac{2GM}{v_\infty^2 r_p}+1}.\) Очевидно, что функция \(a=a(r_p)\) — возрастающая.
Теперь важный момент. Частица падает на Землю, если ее перигей \(r_p\) оказывается меньше радиуса Земли \(R\). Это означает, что должно быть \(a<a_{кр}\), где критическое значение прицельного параметра находится из условия \(r_p=R\), т.е. \(\displaystyle a_{кр}=R\sqrt{\frac{2GM}{v_\infty^2 R}+1}\). Но \(\displaystyle v_2=\sqrt{\frac{2GM}{R}}\) — это вторая космическая скорость. Окончательно, \(\displaystyle a_{кр}=R\sqrt{\frac{v_2^2}{v_\infty^2}+1}\). Подставляя сюда \(v_\infty=2{,}8\) км/с, получаем \(a_{кр}=26400\) км. Все прицельные расстояния меньше чем \(d/2=25000\) км, поэтому весь рой упадет на Землю.
Тут всё верно. Но вы решили не ту задачу.

#68070 zam :В условии задана скорость 2.8 км/с в непосредственной близости от Земли, никак не на бесконечности. Если бы это была скорость вдалеке от Земли, то мы ничего не могли бы сказать про скорость рядом с Землёй. Кометы в Солнечной системе не летают по прямым линиям и с постоянными скоростями. К тому же, если комета летит к Солнцу, то её скорость увеличивается, а если от Солнца, то уменьшается.
Вы о чем? Где в условии задачи говорится о непосредственной близости? Это раз. Второе. Ваша непосредственная близость - это просто пустые слова до тех пор, пока вами не будет указано конкретное расстояние от центра Земли для этой «непосредственной близости». Моя же бесконечность имеет вполне конкретное числовое выражение — это не далее как \(r_\infty=929000\) км от центра Земли, где движение тел в поле Земли можно, особо не заморачиваясь приливным воздействием Солнца, моделировать кривыми конических сечений. Ну подправьте одну из формул в моем решении вот так
\(\displaystyle \frac{1}{2} v_\infty^2- \frac{GM}{r_\infty} = \displaystyle \frac{1}{2} v_p^2- \frac{GM}{r_p}.\)
Сильно при этом изменится ранее вычисленное значение для \(a_{кр}\)? Да почти нисколько.
#68070 zam :
Но вы решили не ту задачу.
Я решил ту задачу. Если не согласны, проведите эксперимент — независимо предложите условие задачи какому-либо специалисту. Решения сравните.







