Движущаяся СО в СТО

#72695 Fedor :#72692 Alex1945 :#72688 Fedor :Как я понимаю, преобразование времени из ПЛ \(t'=\gamma(t-\frac{xV}{c^2})\) тоже предназначено для расчета мгновенного значения местного времени в движущейся ИСО К' по часам неподвижным в этой ИСО. Она говорит, что в момент времени \(t\) движущиеся часы, движущиеся часы, находящиеся в точке \(x\) неподвижной ИСО К, будут показывать местное время \(t'\). А формула сложения скоростей, выведенная из ПЛ и равная \(V'_x=\frac{V_x-V}{1-\frac{V_xV}{c^2}}\) показывает скорость объекта в единицах измерения движущейся ИСО К', по движущимся часам и линейкам этой ИСО. Из этой формулы сложения скоростей следует:
при \(V_x=V\) скорость объекта в неподвижной ИСО \(V'_x=0\);
при \(V_x=0\) скорость объекта в неподвижной ИСО \(V'_x=-V\);
при \(V_x=c\) скорость объекта в неподвижной ИСО \(V'_x=c\).
Если я неправ, то поясните где!
У меня складывается впечатление, что Вы издеваетесь надо мной, притворяясь глупцом. Все три случая скоростей объекта относятся к движущейся СО. Индекс (') прямо говорит об этом.
У Вас складывается ошибочное впечатление. ПЛ как раз и предназначено для перехода описания движения, заданного в неподвижной ИСО, к описанию в движущейся ИСО.
Не понял, неужели Вы считаете, что формула релятивистского сложения скоростей, используемая в СТО, ошибочная или что вытекающие из нее решения для заданных значений \(V_x\) равной 0, c и V, вычислены неправильно?
Потом Вы не указали ошибку в моих вычислениях, которые были проведены для Вашей формулы.

Ваша ошибка состоит в том, что Вы использовали для дифференциала dx’ выражение dx' =Г(dx – Vdt). А моя формула относится к часам, которые не движутся в системе К'. Это означает, что для них dx'=0. Все остальное, что потом Вы пишете – ошибка.
По Вашему выходит, что преобразование координаты \(x'=\gamma(x-Vt)\) в ПЛ применены мной не правильно лишь потому, что в этой точке неподвижно установлены часы движущейся ИСО К'. Потом, в неподвижной ИСО К' не движутся только собственные часы этой ИСО, но относительно движущейся ИСО они движутся со скоростью \(V\), по этому нельзя пренебречь преобразование \(x'=\gamma(x-Vt)\) из ПЛ. Ведь при выводе формулы релятивистского сложения скоростей в СТО использовался именно дифференциал \(dx' = \gamma(dx-Vdt)\).
Потом, если Вы считаете мое решение неправильным, то покажите свое правильное решение для расчета скорости объекта в движущейся ИСО. Тогда можно будет судить о том, чье решение правильное, Ваше или релятивистов.
Как видно из результата вычислений Ваша формула не обеспечивает инвариантность скорости света.
Моя формула является следствием преобразований Эйнштейна, в которых с=const, поэтому моя формула удовлетворяет этому постулату. Поэтому, пока не поймете, что это так, лучше не морочьте мне голову.
Вот это как раз Вам и надо доказать. Одного голословного заявления мало. Нарисовали бы расчетную схему. Например как у меня в теме Зачем физике преобразования Лоренца (ПЛ) .
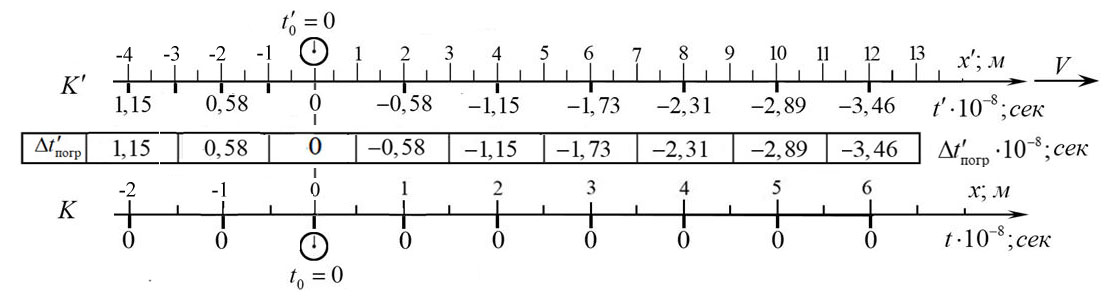
Рисунок 1. Мгновенные значения времени на движущихся и неподвижных часах в начальный момент времени (момент синхронизации).

Рисунок 2. Мгновенные значения времени на движущихся и неподвижных часах в момент времени \(t_2=0,77\cdot 10^{-8}\).
Тогда нам было бы легче понять смысл наших рассуждений и искать ошибки друг у друга.

#72700 Alex1945 :#72695 Fedor :У меня складывается впечатление, что Вы издеваетесь надо мной, притворяясь глупцом. Все три случая скоростей объекта относятся к движущейся СО. Индекс (') прямо говорит об этом.
У Вас складывается ошибочное впечатление. ПЛ как раз и предназначено для перехода описания движения, заданного в неподвижной ИСО, к описанию в движущейся ИСО.
Не понял, неужели Вы считаете, что формула релятивистского сложения скоростей, используемая в СТО, ошибочная или что вытекающие из нее решения для заданных значений \(V_x\) равной 0, c и V, вычислены неправильно?
Вычислены они правильно, но являются скоростями объектов в движущейся СО, а не в неподвижной.
По Вашему выходит, что преобразование координаты \(x'=\gamma(x-Vt)\) в ПЛ применены мной не правильно лишь потому, что в этой точке неподвижно установлены часы движущейся ИСО К'. Потом, в неподвижной ИСО К' не движутся только собственные часы этой ИСО, но относительно движущейся ИСО они движутся со скоростью \(V\), по этому нельзя пренебречь преобразование \(x'=\gamma(x-Vt)\) из ПЛ. Ведь при выводе формулы релятивистского сложения скоростей в СТО использовался именно дифференциал \(dx' = \gamma(dx-Vdt)\).
Дифференциал dx’ это x’1-x’2. Но часы постоянно находятся в точке x’1 или в точке x’2 в зависимости от того, куда Вы их поставили. А в СТО дифференциал dx′=γ(dx−Vdt) написан для тех объектов, которые перемещаются внутри движущейся системы отсчета со скоростью Vx’ между какими-то двумя точками x’1 и x’2 .
Потом, если Вы считаете мое решение неправильным, то покажите свое правильное решение для расчета скорости объекта в движущейся ИСО. Тогда можно будет судить о том, чье решение правильное, Ваше или релятивистов.
Я его уже показал – см #72688
Для движущихся объектов пишем
V x’ =dx’/dt’=(dx-Vdt)/(dt-Vdx/c2)=(dx/dt-V)/(1-Vdx/dt/c2)=(Vx-V)/(1-VVx/c2 ),
где V x — скорость объекта в неподвижной СО, Vx' -скорость того же объекта в движущейся СО, V — скорость СО.
В «моем» случае Vx=V, поэтому Vx' =0.
Моя формула является следствием преобразований Эйнштейна, в которых с=const, поэтому моя формула удовлетворяет этому постулату. Поэтому, пока не поймете, что это так, лучше не морочьте мне голову.
Вот это как раз Вам и надо доказать. Одного голословного заявления мало. Нарисовали бы расчетную схему. Например как у меня в теме Зачем физике преобразования Лоренца (ПЛ) .
Вы предложите еще Эйнштейну это доказать. К сожалению, эта теория для ума не вашего уровня. В ней путаются даже дядьки, которые безошибочно могут получать из нее постоянство скорости света и правильную формулу преобразования скоростей. А Вы, к сожалению, даже физического смысла дифференциала в этой задаче понять не можете. В том, что формулы преобразования Эйнштена и моя формула удовлетворяют постулату о постоянстве скорости света Вам нужно самому разобраться и понять, а пока… не морочте мне голову.

#72701 Fedor :#72700 Alex1945 :#72695 Fedor :У меня складывается впечатление, что Вы издеваетесь надо мной, притворяясь глупцом. Все три случая скоростей объекта относятся к движущейся СО. Индекс (') прямо говорит об этом.
У Вас складывается ошибочное впечатление. ПЛ как раз и предназначено для перехода описания движения, заданного в неподвижной ИСО, к описанию в движущейся ИСО.
Не понял, неужели Вы считаете, что формула релятивистского сложения скоростей, используемая в СТО, ошибочная или что вытекающие из нее решения для заданных значений \(V_x\) равной 0, c и V, вычислены неправильно?
Вычислены они правильно, но являются скоростями объектов в движущейся СО, а не в неподвижной.
Если Ваша формула \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\) предназанчена для вычисления мгновенного значения местного (координатного) времени в движущейся ИСО как и формула \(t'=\gamma(t-\frac{xV}{c^2})\), то она как и последняя должна обеспечивать инвариантность скорости света. Мои же проверочные расчеты показывают, что Ваш вариант не обеспечивает инвариантность скорости света.

По Вашему выходит, что преобразование координаты \(x'=\gamma(x-Vt)\) в ПЛ применены мной не правильно лишь потому, что в этой точке неподвижно установлены часы движущейся ИСО К'. Потом, в неподвижной ИСО К' не движутся только собственные часы этой ИСО, но относительно движущейся ИСО они движутся со скоростью \(V\), по этому нельзя пренебречь преобразование \(x'=\gamma(x-Vt)\) из ПЛ. Ведь при выводе формулы релятивистского сложения скоростей в СТО использовался именно дифференциал \(dx' = \gamma(dx-Vdt)\).
Дифференциал dx’ это x’1-x’2. Но часы постоянно находятся в точке x’1 или в точке x’2 в зависимости от того, куда Вы их поставили. А в СТО дифференциал dx′=γ(dx−Vdt) написан для тех объектов, которые перемещаются внутри движущейся системы отсчета со скоростью Vx’ между какими-то двумя точками x’1 и x’2 .
Не понял, у Вас \(t'\) в формуле \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\) не равен \(t'\) в формуле из ПЛ — \(t'=\gamma(t-\frac{xV}{c^2})\)? Может Вы отказались от преобразования координат в ПЛ, т. е. от \(x'=\gamma(x-Vt)\)? А ведь это преобразование используется в неизменном виде в ТЭЛ, СТО и СЭТ. Между прочим, скорость \(V'_x\) —это мгновенное (точечное) значение скорости объекта, движущегося в движущейся ИСО в точке \(x'\) в рассматриваемый момент.
Потом, если Вы считаете мое решение неправильным, то покажите свое правильное решение для расчета скорости объекта в движущейся ИСО. Тогда можно будет судить о том, чье решение правильное, Ваше или релятивистов.
Я его уже показал – см #72688
Для движущихся объектов пишем
V x’ =dx’/dt’=(dx-Vdt)/(dt-Vdx/c2)=(dx/dt-V)/(1-Vdx/dt/c2)=(Vx-V)/(1-VVx/c2 ),
где V x — скорость объекта в неподвижной СО, Vx' -скорость того же объекта в движущейся СО, V — скорость СО.
В «моем» случае Vx=V, поэтому Vx' =0.
Правильно! Вот по этому для проверки корректности вашего варианта формулы, я использую соответствие ее второму постулату СТО, от которого Вы, как я понял, в данном случае не отказывались и даже утверждали, что вывели свою формулу на основании второго постулата.
Моя формула является следствием преобразований Эйнштейна, в которых с=const, поэтому моя формула удовлетворяет этому постулату. Поэтому, пока не поймете, что это так, лучше не морочьте мне голову.
Вот это как раз Вам и надо доказать. Одного голословного заявления мало. Нарисовали бы расчетную схему. Например как у меня в теме Зачем физике преобразования Лоренца (ПЛ) .
Вы предложите еще Эйнштейну это доказать. К сожалению, эта теория для ума не вашего уровня. В ней путаются даже дядьки, которые безошибочно могут получать из нее постоянство скорости света и правильную формулу преобразования скоростей. А Вы, к сожалению, даже физического смысла дифференциала в этой задаче понять не можете. В том, что формулы преобразования Эйнштена и моя формула удовлетворяют постулату о постоянстве скорости света Вам нужно самому разобраться и понять, а пока… не морочте мне голову.
Если Вы разобрались в СТО лучше меня, то Вам не стоит большого труда проверить вашу формулу на соответствие второму постулату. Я считаю, что предложенная мной проверка на соответствие второму постулату подходить лучше всего. Потом я не увидел формулу сложения скоростей, полученную для вашего варианта формулы преобразования времени.
Кстати, был бы Вам признателен, если бы Вы поучаствовали в теме Зачем физике преобразования Лоренца (ПЛ) со своими критическими замечаниями.

#72702 Alex1945 :#72701 Fedor :Если Ваша формула \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\) предназанчена для вычисления мгновенного значения местного (координатного) времени в движущейся ИСО как и формула \(t'=\gamma(t-\frac{xV}{c^2})\), то она как и последняя должна обеспечивать инвариантность скорости света. Мои же проверочные расчеты показывают, что Ваш вариант не обеспечивает инвариантность скорости света.

Моя формула – это формула Эйнштейна и предназначена она не для определения мгновенного значения времени, а для определения показаний конкретного экземпляра находящихся в движущейся СО часов в любой момент времени t неподвижной системы отсчета. Ваши «проверочные расчеты» выполняются на основе полученной не мной, а Вами, неправильной формулы преобразования скоростей. Моя формула преобразования времени не может быть использована для вывода формулы преобразования скоростей, так как в ней отсутствуют движущиеся объекты внутри СО K'. Из нее можно получить только Vx’ =0.
Не понял, у Вас \(t'\) в формуле \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\) не равен \(t'\) в формуле из ПЛ — \(t'=\gamma(t-\frac{xV}{c^2})\)? Может Вы отказались от преобразования координат в ПЛ, т. е. от \(x'=\gamma(x-Vt)\)? А ведь это преобразование используется в неизменном виде в ТЭЛ, СТО и СЭТ. Между прочим, скорость \(V'_x\) —это мгновенное (точечное) значение скорости объекта, движущегося в движущейся ИСО в точке \(x'\) в рассматриваемый момент.
Вторая формулы для t’ – это одна и та же формула, в которой переменная х представляет координату движущихся часов во времени. Вы можете подставить это выражение для х в формулу для x' и получите x’ =γx0 cтартовую координату часов в движущейся системе отсчета. dx’ =0 от этой координаты, а Вы ею манипулируете будто часы движутся внутри системы отсчета.
Потом, если Вы считаете мое решение неправильным, то покажите свое правильное решение для расчета скорости объекта в движущейся ИСО. Тогда можно будет судить о том, чье решение правильное, Ваше или релятивистов.
Я его уже показал – см #72688
Для движущихся объектов пишем
V x’ =dx’/dt’=(dx-Vdt)/(dt-Vdx/c2)=(dx/dt-V)/(1-Vdx/dt/c2)=(Vx-V)/(1-VVx/c2 ),
где V x — скорость объекта в неподвижной СО, Vx' -скорость того же объекта в движущейся СО, V — скорость СО.
В «моем» случае Vx=V, поэтому Vx' =0.
Правильно! Вот по этому для проверки корректности вашего варианта формулы, я использую соответствие ее второму постулату СТО, от которого Вы, как я понял, в данном случае не отказывались и даже утверждали, что вывели свою формулу на основании второго постулата.
О качестве вашей проверки см. текст выше.
Я не знаю вашего образования и какой там Вы имеете Диплом или Свидетельство, но судя по Вашему пониманию преобразований и манипуляциям с ними, я не перевел бы Вас из четвертого класса школы в пятый.
Будьте здоровы , досвидания.

#72705 Fedor :#72702 Alex1945 :#72701 Fedor :Если Ваша формула \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\) предназанчена для вычисления мгновенного значения местного (координатного) времени в движущейся ИСО как и формула \(t'=\gamma(t-\frac{xV}{c^2})\), то она как и последняя должна обеспечивать инвариантность скорости света. Мои же проверочные расчеты показывают, что Ваш вариант не обеспечивает инвариантность скорости света.

Моя формула – это формула Эйнштейна и предназначена она не для определения мгновенного значения времени, а для определения показаний конкретного экземпляра находящихся в движущейся СО часов в любой момент времени t неподвижной системы отсчета.
А что есть мгновенное значение местного (координатного) времени? Формула \(t'=\gamma(t-\frac{xV}{c^2})\) определяет мгновенное значение местного времени часов движущейся ИСО находящихся в момент t неподвижной ИСО в точке x неподвижной ИСО. Местное (координатное) время \(t'=F(t,x)\) является функцией двух независимых переменных. Другими словами в моментможет находиться только один конкретный экземпляр часов движущихся ИСО, т. е. в каждый момент времени t в точке x будет находиться другой экземпляр движущихся часов.
Ваши «проверочные расчеты» выполняются на основе полученной не мной, а Вами, неправильной формулы преобразования скоростей. Моя формула преобразования времени не может быть использована для вывода формулы преобразования скоростей, так как в ней отсутствуют движущиеся объекты внутри СО K'. Из нее можно получить только Vx’ =0.
Так я привел два результата вывода формулы сложения скоростей для правильного и неправильного толкования вашей формулы, т. е. для \(t'=\gamma(t-\frac{(x+Vt)V}{c^2})\), для которой \(V'_x=\frac{V_x-V}{1-\frac{V}{c}-\frac{V_xV}{c^2}}\) и \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\), для которой \(V'_x=\frac{V_x-V}{1-\frac{V^2}{c^2}}\). И что оба неправильные? Может покажите почему нельзя получить из вашей формулы скорость \(V'_x\) в общем виде.
Не понял, у Вас \(t'\) в формуле \(t'=\gamma(t-\frac{(x_0+Vt)V}{c^2})\) не равен \(t'\) в формуле из ПЛ — \(t'=\gamma(t-\frac{xV}{c^2})\)? Может Вы отказались от преобразования координат в ПЛ, т. е. от \(x'=\gamma(x-Vt)\)? А ведь это преобразование используется в неизменном виде в ТЭЛ, СТО и СЭТ. Между прочим, скорость \(V'_x\) —это мгновенное (точечное) значение скорости объекта, движущегося в движущейся ИСО в точке \(x'\) в рассматриваемый момент.
Вторая формулы для t’ – это одна и та же формула, в которой переменная х представляет координату движущихся часов во времени. Вы можете подставить это выражение для х в формулу для x' и получите x’ =γx0 cтартовую координату часов в движущейся системе отсчета. dx’ =0 от этой координаты, а Вы ею манипулируете будто часы движутся внутри системы отсчета.
Я решаю вашу задачу в общем виде. Если мое решение правильное, то подставляя разные значения x и t можно получить любой вариант решения.
П отом, если Вы считаете мое решение неправильным, то покажите свое правильное решение для расчета скорости объекта в движущейся ИСО. Тогда можно будет судить о том, чье решение правильное, Ваше или релятивистов.
Я его уже показал – см #72688
Для движущихся объектов пишем
V x’ =dx’/dt’=(dx-Vdt)/(dt-Vdx/c2)=(dx/dt-V)/(1-Vdx/dt/c2)=(Vx-V)/(1-VVx/c2 ),
где V x — скорость объекта в неподвижной СО, Vx' -скорость того же объекта в движущейся СО, V — скорость СО.
В «моем» случае Vx=V, поэтому Vx' =0.
Правильно! Вот по этому для проверки корректности вашего варианта формулы, я использую соответствие ее второму постулату СТО, от которого Вы, как я понял, в данном случае не отказывались и даже утверждали, что вывели свою формулу на основании второго постулата.
О качестве вашей проверки см. текст выше.
Я не знаю вашего образования и какой там Вы имеете Диплом или Свидетельство, но судя по Вашему пониманию преобразований и манипуляциям с ними, я не перевел бы Вас из четвертого класса школы в пятый.
Будьте здоровы , досвидания.
То есть Вы отказались показать/доказать, как Вы получаете выполнение второго постулата в вашем варианте преобразования времени! Тогда, может, поясните: зачем Вы открыли эту тему? А переход с математики на личность — это далеко не научный подход, к тому же не имеющий доказательной силы.

#72735 Alex1945 :То есть Вы отказались показать/доказать, как Вы получаете выполнение второго постулата в вашем варианте преобразования времени! Тогда, может, поясните: зачем Вы открыли эту тему? А переход с математики на личность — это далеко не научный подход, к тому же не имеющий доказательной силы.
Доказательная сила состоит в непонимании моих многократных пояснений. Например, при выводе формулы сложения скоростей с использованием моей формулы Вы пользуетесь формулой преобразования x'=Г(x-Vt) и берете от нее дифференциал, зная, что в моей формуле x=x0+Vt. Неужели трудно сообразить, что, подставив такое значение х, Вы получаете x' = Гx0 ? Дифференциал от него равен нулю. И на этом заканчиваются все дальнейшие манипуляции. А Вы продолжаете получать хрен знает что. И это только один эпизод.
А тему я открыл для тех, кто что-то в этой теме понимает и подобных глупостей не допускает.




