Парадокс собственного хода трех часов. Схема Смородинского.

Парадокс собственного хода трех часов. Схема Смородинского.
Парадокс часов (близнецов) в СТО известен давно.У противников СТО вызывала сомнение симметричность РЭ. То есть тот факт, что в двух одинаковых ИСО, движущихся относительно друг друга, часы в движущейся ИСО замедляют свой ход, причем это замедление должно быть симметричным. Ведь любая, из этих двух ИСО, может быть принята за неподвижную, и замедлять свой ход уже будут часы, которые теперь стали движущимися.
Спрашивается: возможно, ли такое симметричное замедление в реальности? Вызывал сомнение тот факт, что часы этих двух ИСО могли (или должны) в реальности одновременно идти быстрее и медленнее друг друга. В СТО это все объясняли процедурой измерения с использованием относительной одновременности (ОО). В этом случае отрезок времени, отсчитанный одними движущимися часами, сравнивался с отрезком времени, отсчитанным по двум неподвижным часам, синхронизированными по специальной методике, обеспечивающей ОО.
Парадокс часов был задуман для того, что показать противоречивость объяснения симметричности замедления времени, существование которой заявлено в СТО.
Смысл парадокса часов заключался в желании критиков СТО исключить из процесса измерения ошибки, вызываемые использованием ОО, которая, по утверждению релятивистов, обеспечивала симметричность РЭ. Для этого из рассуждений необходимо было исключить ОО, которая возникала только при наличии в составе эксперимента нескольких разноместных часов, синхронизированных световым сигналом.
Я. А. Смородинский предложил вариант парадокса часов, который бы полностью соответствовал СТО.
Смородинский предложил свой вариант для упрощения вариантов, в которых движущиеся часы не все время двигались равномерно и прямолинейно, а еще подвергались разгонам и торможениям.
Для своего варианта Смородинский делает неправильный вывод: "… В таком опыте участвуют трое часов, и видимого парадокса не возникает."
Однако, хотя в данном случае описание происходит точно в рамках СТО, но противоречия при этом все-таки возникают.
Мысленный эксперимент с тремя часами по схеме Смородинского наглядно подтверждает, что замедление хода движущихся часов, принятое для объяснения результатов ММ, противоречит первому постулату СТО, который требует, чтобы собственный ход тождественных часов был одинаковым во всех ИСО.
Предлагаю рассмотреть вариант с тремя часами подробнее.


Перевожу на человеческий язык.
Задача сто-009
Имеются трое часов – А, В и С.
Им соответствуют три ИСО – (А), (В) и ( С), в которых соответствующие часы покоятся.
Уравнения движения часов в ИСО (А):
\(x_A^{(A)}\left( t^{A} \right)=0 \\x_B^{(A)}\left( t^{A} \right)=vt^{(A)} \\x_C^{(A)}\left( t^{A} \right)=L-vt^{(A)}\)
Имеются три события:
— «АВ» — встреча часов А и В;
— «АС» — встреча часов А и С;
— «ВС» — встреча часов В и С.
Нужно определить результаты измерения промежутков времени:
— между событиями АВ и АС часами А \(\Delta t_{AB-AC}^{(A)}\);
— между событиями АВ и BС часами B \(\Delta t_{AB-BC}^{(B)}\) ;
— между событиями АС и ВС часами C \(\Delta t_{AC-BC}^{©}\) .
Пойдёт?

С вашего позволения, картинкой.
Решение задачи сто-009


#66969 zam :Перевожу на человеческий язык.
Задача сто-009
Имеются трое часов – А, В и С.
Им соответствуют три ИСО – (А), (В) и ( С), в которых соответствующие часы покоятся.
Уравнения движения часов в ИСО (А):
\(x_A^{(A)}\left( t^{A} \right)=0 \\x_B^{(A)}\left( t^{A} \right)=vt^{(A)} \\x_C^{(A)}\left( t^{A} \right)=L-vt^{(A)}\)
Имеются три события:
— «АВ» — встреча часов А и В;
— «АС» — встреча часов А и С;
— «ВС» — встреча часов В и С.
Нужно определить результаты измерения промежутков времени:
— между событиями АВ и АС часами А \(\Delta t_{AB-AC}^{(A)}\);
— между событиями АВ и BС часами B \(\Delta t_{AB-BC}^{(B)}\) ;
— между событиями АС и ВС часами C \(\Delta t_{AC-BC}^{©}\) .
Пойдёт?
Не пойдет. Вы изменили порядок протекания эксперимента и мои обозначения, что только запутает поиск ошибок в моем и Вашем варианте задачи. Так давайте сначала разберемся с моим решением и моей расчетной схемой.

Решим задачу для случая, когда неподвижной будет ИСО с часами А, т. е. будем пользоваться единицами измерения ИСО А. Для удобства немного уточню условные обозначения для моментов собственного времени и для отрезков собственного времени.
Событие 1. Момент встречи часов А и С в точке А. \(t_{A_1}=t_{C_1}=0\) ; \(x_{A}=0\).
Событие 2. Момент встречи часов В и С в точке D. \(t_{B_2}=0\) ; \(t_{C_2}=l/V\); \(x_{D}=l\).
Событие 3. Момент встречи часов В и A в точке A. \(t_{B_3}=l/V\) ; \(t_{A_3}=2l/V\); \(x_{A}=0\).
Вариант 1. В задаче для часов выполняется первый постулат СТО, т. е. все часы имеют одинаковый (инвариантный) собственный ход. Тогда отрезки собственного времени будут равны:
\(\Delta t_B=t_{B_3}-t_{B_2}=l/V\) ;
\(\Delta t_C=t_{C_2}-t_{C_1}=l/V\);
\(\Delta t_A=t_{A_3}-t_{A_1}=\Delta t_B + \Delta t_C=2l/V\).
Вариант 2. В задаче для часов первый постулат СТО не выполняется, т. е. согласно результатам М-М движущиеся часы идут медленнее неподвижных в \(\gamma\) раз. Тогда отрезки собственного времени будут равны:
\(\Delta t'_C=t'_{C_2}-t'_{C_1}=\frac{l}{\gamma V}\);
\(\Delta t_B^"=t^"_{B_3}-t^"_{B_2}=\frac {l}{\gamma V}\) ;
\(\Delta t_A=\frac {2l}{V}>t_{A_3}-t_{A_1}=\Delta t_B^" + \Delta t'_C=\frac {2l}{\gamma V}\).
Вариант 3. В задаче для часов первый постулат СТО не выполняется, а движущиеся часы изменяют собственный ход согласно ПЛ. Вот этот вариант и рассчитайте с моими обозначениями и потом сравним наши результаты.

#66971 zam :С вашего позволения, картинкой.
Решение задачи сто-009

Перед тем как приступить к изучению Вашего решения, я хотел бы окончательно разобраться с моим решением в посте. Решение в нем значительно проще Вашего. А Ваше решение — это попытка решить мою задачу при помощи ПЛ, т. е. вариант 3 из исходного поста, и мы с Вами обязательно рассмотрим, после окончательного решения по первым двум вариантам. А первые два варианта решения не имеют математических ошибок, а отличаются только теориями, в рамках которых результаты эксперимента рассматриваются.
Жду от Вас конкретной критики первых двух вариантов поста 66972.

#66972 Alex1945 :#66969 zam :Перевожу на человеческий язык.
Пойдёт?
Не пойдет. Вы изменили порядок протекания эксперимента и мои обозначения, что только запутает поиск ошибок в моем и Вашем варианте задачи.
Порядок проведения эксперимента не изменён. Обозначения сделаны удобными. Если вам очень хочется, можете написать соответствия между вашими и моими обозначениями.
Так давайте сначала разберемся с моим решением и моей расчетной схемой.
Нет. Вы не желаете решать задачу (у вас нет решения, так что и разбираться не с чем). Разбирайтесь с моим. Если можете, укажите на ошибки в решении.

#66974 Alex1945 :#66971 zam :Решение задачи сто-009
Перед тем как приступить к изучению Вашего решения, я хотел бы окончательно разобраться с моим решением в посте.
Там нет решения. Вы что же, не знаете, что такое решение?
Жду от Вас конкретной критики первых двух вариантов поста 66972.
То, где вы пытаетесь решать в рамках ТЭЛ, я критиковать не могу, потому что ТЭЛ не знаю. К тому же, это оффтоп, потому что раздел называется «Элементы СТО».
В рамках СТО у вас даже попытки решения нет. Что же там критиковать?

#67028 zam :#66972 Alex1945 :#66969 zam :Перевожу на человеческий язык.
Пойдёт?
Не пойдет. Вы изменили порядок протекания эксперимента и мои обозначения, что только запутает поиск ошибок в моем и Вашем варианте задачи.
Порядок проведения эксперимента не изменён. Обозначения сделаны удобными. Если вам очень хочется, можете написать соответствия между вашими и моими обозначениями.
В исходнике сначала в момент встречаются часы С и А, потом С и В, и в конце эксперимента часы А и В. Вы специально изменили порядок эксперимента, чтобы непонятней было и чтобы меньше было желающих вникать в суть вашего решения?
Так давайте сначала разберемся с моим решением и моей расчетной схемой.
Нет. Вы не желаете решать задачу (у вас нет решения, так что и разбираться не с чем). Разбирайтесь с моим. Если можете, укажите на ошибки в решении.
Указал, что Ваша задача не соответствует моей. Исправляйте порядок протекания эксперимента в соответствии с исходником. Потом поговорим.

Александр, ты опять народ мучаешь своим Смородинским?
Ну и что, тебе на этом форуме что-то нового сказали такого чего ты не слышал уже сто раз?

#67029 zam :#66974 Alex1945 :#66971 zam :Решение задачи сто-009
Перед тем как приступить к изучению Вашего решения, я хотел бы окончательно разобраться с моим решением в посте.
Там нет решения. Вы что же, не знаете, что такое решение?
Решение есть и оно очень простое — см. исходный пост.

Проблема в понимании физического смысла эксперимента по схеме Смородинского. В этом решении учтено, что в СТО отрезки собственного времени во всех ИСО идут одинаково (инвариантны).

или

Жду от Вас конкретной критики первых двух вариантов поста 66972.
То, где вы пытаетесь решать в рамках ТЭЛ, я критиковать не могу, потому что ТЭЛ не знаю. К тому же, это оффтоп, потому что раздел называется «Элементы СТО».
Просто Вы принимаете ТЭЛ за СТО, поэтому и все Ваши рассуждения о физическом смысле СТО ошибочные. В исходнике решение, соответствующее Вашему пониманию СТО приведено в п.1 исходного поста.

В рамках СТО у вас даже попытки решения нет. Что же там критиковать?
Решение в рамках СТО повторено на рисунке выше — см. п. 2 исходного поста. Вам, чтобы доказать ошибочность моего решения, надо только доказать, что в СТО собственные отрезки времени часов во всех ИСО неинвариантные.

Александр, тебе сто раз уже повторяли — по СТО у тебя решения нет и никогда не было. То что ты называешь «решил по СТО» к настоящей СТО никакого отношения вообще не имеет.

#67028 zam :#66972 Alex1945 :#66969 zam :Перевожу на человеческий язык.
Пойдёт?
Не пойдет. Вы изменили порядок протекания эксперимента и мои обозначения, что только запутает поиск ошибок в моем и Вашем варианте задачи.
Порядок проведения эксперимента не изменён. Обозначения сделаны удобными. Если вам очень хочется, можете написать соответствия между вашими и моими обозначениями.
Так давайте сначала разберемся с моим решением и моей расчетной схемой.
Нет. Вы не желаете решать задачу (у вас нет решения, так что и разбираться не с чем). Разбирайтесь с моим. Если можете, укажите на ошибки в решении.
Почему я должен разбираться в Вашей задаче, если я могу только предполагать расчетную схему Вашей задачи, но если в ней Вы перепутали только последовательность событий, то Вы даже в этом случае не смогли правильно определить координаты событий в ИСО А!
Ваши координаты трех событий эксперимента в ИСО А:

правильные координаты по Вашей схеме по всей видимости должны выглядеть так:

Поправьте меня на Вашей схеме, если я не прав!
Если я прав, то решите Вашу задачу с уточненными координатами.
В моей задаче координаты трех событий будут

отредактировал(а) Alex1945: 2024-10-05 18:08 GMT

Поскольку я, видимо, не дождусь решения задачи этой темы при помощи ПЛ, то предлагаю свой вариант решения.

Если что непонятно, то спрашивайте, поясню по мере моих возможностей. Прошу обратить внимание на третий вариант результатов решения, который противоречит по физическому смыслу и СТО, и ТЭЛ. Вот почему я не хотел его приводить сразу. Потому что это приведет к обсуждению не парадокса часов, а противоречий ПЛ. Тем более, что это решение противоречит расчетной схеме и описанию эксперимента, так как в точке D нужно установить никому не нужные часы D, т. е. перевести задачу о сравнении трех отрезков собственного времени к задаче о сравнении отрезков координатного и собственного времени, что лишает эксперимент по схеме Смородинского главного достоинства, т. е. отсутствия искажения результатов расчетов из-за ошибок световой синхронизации в движущихся ИСО.

#67074 Alex1945 :#67028 zam :Разбирайтесь с моим. Если можете, укажите на ошибки в решении.
Почему я должен разбираться в Вашей задаче, если я могу только предполагать расчетную схему Вашей задачи,
Расчётная схема приведена полностью.
но если в ней Вы перепутали только последовательность событий,
Изменены наименования часов, больше ничего. Да, ещё начальное расстояние обозначено не 2L, а L.
то Вы даже в этом случае не смогли правильно определить координаты событий в ИСО А!
Ваши координаты трех событий эксперимента в ИСО А:

правильные координаты по Вашей схеме по всей видимости должны выглядеть так:

Поправьте меня на Вашей схеме, если я не прав!
Поправляю. Вот диаграмма Минковского к задаче:
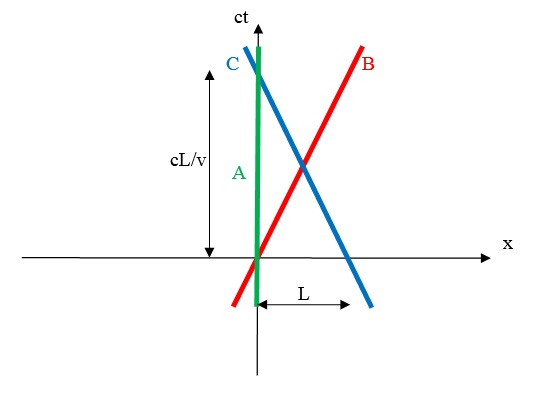
Составлена в точном соответствии с условиями задачи сто-009 ( #66969 ).
Из неё наглядно видно, что координаты событий в ИСО (А) указаны правильно.
Если я прав, то решите Вашу задачу с уточненными координатами.
Вы не правы.
В моей задаче координаты трех событий будут

А вот диаграмма Минковского по вашим условиям:
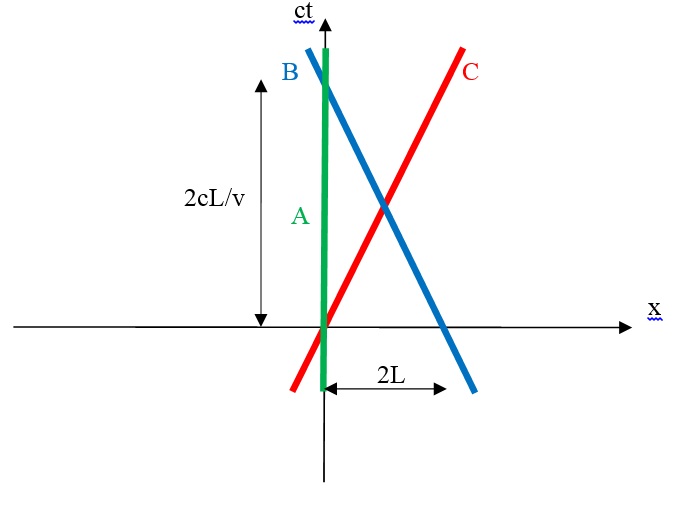
Как видите, принципиальной разницы нет.

#67315 Alex1945 :Поскольку я, видимо, не дождусь решения задачи этой темы при помощи ПЛ, то предлагаю свой вариант решения.
Это уже кое что!
Вот только система обозначений у вас крайне неудобная. Обозначили часы (и их собственные системы отсчёта) буквами — так и продолжайте. Обозначили события цифрами — так и продолжайте.
Я перепишу ваши выкладки в нормальных обозначениях.
Я перепишу ваши выкладки в нормальных обозначениях.
Если что непонятно, то спрашивайте, поясню по мере моих возможностей.
Всё понятно. Только у вас ошибка.
Для перехода из ИСО (А) в ИСО (штрих) и в ИСО (два штриха) вы используете одну и ту же формулу: \(\gamma\left( t-\frac{Vx}{c^2}\right)\).
Но! ИСО (штрих) и ИСО (два штриха) двигаются относительно ИСО (А) в противоположных направлениях. Поэтому для одной должно быть \(\gamma\left( t-\frac{Vx}{c^2}\right)\), а для другой \(\gamma\left( t+\frac{Vx}{c^2}\right)\) .
Проверяйте.

#67358 zam :#67315 Alex1945 :Поскольку я, видимо, не дождусь решения задачи этой темы при помощи ПЛ, то предлагаю свой вариант решения.
Это уже кое что!
Вот только система обозначений у вас крайне неудобная. Обозначили часы (и их собственные системы отсчёта) буквами — так и продолжайте. Обозначили события цифрами — так и продолжайте.
Это Ваше личное мнение. А на мой взгляд мое последнее обозначение логичней и решение получилось короче.

Я перепишу ваши выкладки в нормальных обозначениях.

Я перепишу ваши выкладки в нормальных обозначениях.
Если что непонятно, то спрашивайте, поясню по мере моих возможностей.
Всё понятно. Только у вас ошибка.
Для перехода из ИСО (А) в ИСО (штрих) и в ИСО (два штриха) вы используете одну и ту же формулу: \(\gamma\left( t-\frac{Vx}{c^2}\right)\).
Но! ИСО (штрих) и ИСО (два штриха) двигаются относительно ИСО (А) в противоположных направлениях. Поэтому для одной должно быть \(\gamma\left( t-\frac{Vx}{c^2}\right)\), а для другой \(\gamma\left( t+\frac{Vx}{c^2}\right)\) .
Проверяйте.
Но мой взгляд ошибка у Вас. Знак поправки \(\frac{Vx}{c^2}\) зависит от направления движения движущейся ИСО и знак (-) показывает насколько должны отстать часы удаленные на расстояние \(x\) по направлению движения ИСО относительно неподвижной ИСО, поэтому в обоих случаях должна использоваться формула \(\gamma\left( t-\frac{Vx}{c^2}\right)\). См. рисунок ниже, где показано движение светового сигнала при синхронизации часов в ИСО С и ИСО В.


#67367 Alex1945 :#67358 zam :Для перехода из ИСО (А) в ИСО (штрих) и в ИСО (два штриха) вы используете одну и ту же формулу: \(\gamma\left( t-\frac{Vx}{c^2}\right)\).
Но! ИСО (штрих) и ИСО (два штриха) двигаются относительно ИСО (А) в противоположных направлениях. Поэтому для одной должно быть \(\gamma\left( t-\frac{Vx}{c^2}\right)\), а для другой \(\gamma\left( t+\frac{Vx}{c^2}\right)\) .
Проверяйте.
Но мой взгляд ошибка у Вас.
А почему бы вам не посмотреть учебник?
Знак поправки \(\frac{Vx}{c^2}\) зависит от направления движения движущейся ИСО и знак (-) показывает насколько должны отстать часы удаленные на расстояние \(x\) по направлению движения ИСО относительно неподвижной ИСО, поэтому в обоих случаях должна использоваться формула \(\gamma\left( t-\frac{Vx}{c^2}\right)\).
\(\frac{Vx}{c^2}\) — это не поправка.
Используется форма преобразований Лоренца
\( \left\{\begin{matrix}x'=\gamma \left ( x-vt \right ) \\t'=\gamma \left ( t-\frac{vx}{c^2} \right )\end{matrix}\right.\)
это их простейшая форма.
Применима только в том случае, когда пространственные координатные оси двух систем отсчёта коллинеарны, а начала остсчета систем координат совпадают, вектор скорости движения одной ИСО относительно другой ИСО направлен вдоль оси x.
Что тут обозначает буква v? Это проекция скорости движения штирихованной ИСО относительно нештрихованной на ось x. Если скорость направлена туда же, куда и ось x, тогда используются выше приведённые соотношения.
А если скорость направлена встречно оси x? Тогда проекция вектора скорости на ось x будет отрицательна.
У вас часы В и часы С двигаются встречно. То есть, проекции их скоростей на ось x имеют противоположные знаки.

#67387 zam :#67367 Alex1945 :#67358 zam :Для перехода из ИСО (А) в ИСО (штрих) и в ИСО (два штриха) вы используете одну и ту же формулу: \(\gamma\left( t-\frac{Vx}{c^2}\right)\).
Но! ИСО (штрих) и ИСО (два штриха) двигаются относительно ИСО (А) в противоположных направлениях. Поэтому для одной должно быть \(\gamma\left( t-\frac{Vx}{c^2}\right)\), а для другой \(\gamma\left( t+\frac{Vx}{c^2}\right)\) .
Проверяйте.
Но мой взгляд ошибка у Вас.
А почему бы вам не посмотреть учебник?
Знак поправки \(\frac{Vx}{c^2}\) зависит от направления движения движущейся ИСО и знак (-) показывает насколько должны отстать часы удаленные на расстояние \(x\) по направлению движения ИСО относительно неподвижной ИСО, поэтому в обоих случаях должна использоваться формула \(\gamma\left( t-\frac{Vx}{c^2}\right)\).
\(\frac{Vx}{c^2}\) — это не поправка.
Используется форма преобразований Лоренца
\( \left\{\begin{matrix}x'=\gamma \left ( x-vt \right ) \\t'=\gamma \left ( t-\frac{vx}{c^2} \right )\end{matrix}\right.\)
это их простейшая форма.
Применима только в том случае, когда пространственные координатные оси двух систем отсчёта коллинеарны, а начала остсчета систем координат совпадают, вектор скорости движения одной ИСО относительно другой ИСО направлен вдоль оси x.
Что тут обозначает буква v? Это проекция скорости движения штирихованной ИСО относительно нештрихованной на ось x. Если скорость направлена туда же, куда и ось x, тогда используются выше приведённые соотношения.
А если скорость направлена встречно оси x? Тогда проекция вектора скорости на ось x будет отрицательна.
У вас часы В и часы С двигаются встречно. То есть, проекции их скоростей на ось x имеют противоположные знаки.
Вы считаете, наклоны стрелок на часах ИСО В и ИСО С не соответствуют отставанию часов, расположенных по направлению движения?
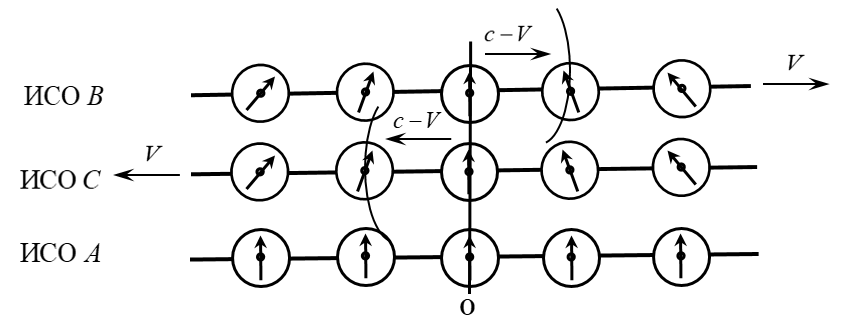
Приведите свой правильный вариант. Но, на мой взгляд, эта схема с разноместными часами соответствует ПЛ, но противоречит схеме исходного поста, в которой рассматриваются исключительно отрезки собственного времени, которые согласно СТО — инвариантные, т. е. одинаковые во всех ИСО.
Поэтому не стоит искажать и усложнять известную задачу вводом в расчетную схему дополнительных часов, к тому же с неправильной синхронизацией. Ведь тема так и называется «Парадокс собственного хода трех часов. Схема Смородинского».
отредактировал(а) Alex1945: 2024-10-16 22:40 GMT

#67403 Alex1945 :Вы считаете, наклоны стрелок на часах ИСО В и ИСО С не соответствуют отставанию часов, расположенных по направлению движения?

Я не понимаю, что тут у вас нарисовано.
Приведите свой правильный вариант.
В вам привёл полное решение вашей задачи ( #67358 ). Вы обнаружили в нём ошибки? Тогда расскажите, в чём они и как надо.
Поэтому не стоит искажать и усложнять известную задачу вводом в расчетную схему дополнительных часов, к тому же с неправильной синхронизацией.
Какие дополнительные часы я ввёл?
Ведь тема так и называется «Парадокс собственного хода трех часов. Схема Смородинского».
Вот я и показал — никакого «парадокса» в этой схеме нет. Это я про СТО. В ТЭЛ я не разбираюсь (может, там он и есть, но тогда это очень плохо для ТЭЛ).

#67420 zam :#67403 Alex1945 :Вы считаете, наклоны стрелок на часах ИСО В и ИСО С не соответствуют отставанию часов, расположенных по направлению движения?

Я не понимаю, что тут у вас нарисовано.
Это потому что для часов ИСО С стрелки изображены ошибочно. Правильный рисунок будет выглядеть, когда во всех ИСО стрелки часов вращаются в одном направлении (по часовой стрелке) — см. ниже.

Нижний ряд часов — это ряд часов в неподвижной ИСО А в нулевой момент, когда все стрелки установлены на ноль.
Средний ряд часов — это ряд часов в движущейся ИСО С в нулевой момент, когда начала координат совместились, а стрелки часов в начале ИСО А и ИСО С установлены на ноль. Часы ИСО С синхронизированы световым сигналом по методике СТО, при которой часы, удаленные от начала координат в направлении движения, отстают от часов начала отсчета.
Верхний ряд часов — это ряд часов в движущейся ИСО В в нулевой момент, в которой тоже часы, расположенные по направлению движения ИСО и синхронизированные световым сигналом, отстают от часов от часов начала координат.
Приведите свой правильный вариант.
В вам привёл полное решение вашей задачи ( #67358 ). Вы обнаружили в нём ошибки? Тогда расскажите, в чём они и как надо.
Вы используете выражение \(t'=\gamma(t-\frac {Vx}{c^2})\), где выражение \(\pm\gamma \frac {Vx}{c^2}\) — это результат световой синхронизации, зависящий от положения часов в точке D относительно начала координат движущейся ИСО и направления движения движущихся часов относительно неподвижной ИСО А — см. рисунок выше. А это значит, что Вы ввели в расчет показания несуществующих часов в точке D, что противоречит условиям эксперимента.
А вторая Ваша ошибка в том, что Вы используете вместо выражения \(t'=\gamma(t-\frac {Vx}{c^2})\) для обеих ИСО, для одной ИСО \(t'=\gamma(t-\frac {Vx}{c^2})\), а для другой \(t'=\gamma(t+\frac {Vx}{c^2})\) — см. рисунок выше.
Поэтому не стоит искажать и усложнять известную задачу вводом в расчетную схему дополнительных часов, к тому же с неправильной синхронизацией.
Какие дополнительные часы я ввёл
Часы в точке D, которым присвоили значение с поправкой синхронизации \(\pm\gamma \frac {Vx}{c^2}\). То есть показаниям несуществующих в эксперименте часам в точке D присвоили поправку непроведенной синхронизации световым сигналом.
Ведь тема так и называется «Парадокс собственного хода трех часов. Схема Смородинского».
Вот я и показал — никакого «парадокса» в этой схеме нет. Это я про СТО. В ТЭЛ я не разбираюсь (может, там он и есть, но тогда это очень плохо для ТЭЛ).
Во-первых, Вы рассматривали свою схему с несуществующими в исходнике часами D, а во-вторых, неправильно учитывали поправку синхронизации. Да и вообще, часы в точке D не нужны, так как от часов В и С время в ИСО А не передается, и между собой в исходном варианте часы В и С показаниями времени не обмениваются. Часы С в этот момент останавливаются, а часы В с нуля запускаются.
А вариант с расчетом по ПЛ — это камешек в сторону не интересующей Вас ТЭЛ, т. е. и в ТЭЛ есть противоречие — см. тему. Чему противоречат преобразования Лоренца в ТЭЛ.
Но главная ошибка у Вас в том, что Вы забываете о первом постулате СТО, согласно которому собственное время часов А, В и С является инвариантом, т. е. все физические процессы должны протекать с одинаковой скоростью. Например, частота собственных колебаний в цезиевых часах должна быть инвариантом, поэтому и часы А, В и С, в которых в качестве эталона принята эта частота, должны тикать с этой частотой во всех ИСО.
В чем есть ценность схемы Смородинского, что она позволяет доказать существование парадокса часов в СТО и позволяет экспериментально отличать СТО от ТЭЛ или СЭТ.
Кстати, на Астофоруме тему https://astronomy.ru/forum/index.php/topic,209504.0.html меня забанили за распространение невежества, а точнее за цитаты из учебников, которые сторонники СТО считали результатом некомпетентности/невнимательности авторов учебников. Но главная причина в том, что сторонники СТО не понимают, как это инвариантность собственного времени может противоречить ПЛ и наблюдениям за быстодвижущимися мюонами. Они так и не смогли прийти к косолидированному мнению, т. е. выбрать вариант правильного решения задачи исхоного поста:
1. \(\Delta t_A=\Delta t_B+\Delta t_C\) — соответствует первому постулату СТО
или
2. \(\Delta t_A>\Delta t_B+\Delta t_C\).- соответствует ПЛ и наблюдениям за быстродвижущимися мюонами.
отредактировал(а) Alex1945: 2025-12-09 09:05 GMT

Предлагаю рассмотреть цитату из книги Угарова В.А. «Специальная теория относительности», 1977 г., которую на Астрофоруме признали распространением мной невежества, тогда как я считаю это правильным пониманием автором книги физической сути собственного времени.

Согласно этой цитате отрезки собственного времени полученные в исходнике этой темы должны выглядеть \(\Delta t_A=\Delta t_B+\Delta t_C\), что соответствует первому постулату СТО (ПО), но противоречит наблюдениям за быстродвижущимися мюонами.
Другими словами это и есть вариант парадокса часов, из которого исключено влияние ускорений и разворота движущихся часов. Следовательно, эксперимент по этой схеме позволяет отличить СТО от ТЭЛ по полученным результатам.

Приведенная вами схема:
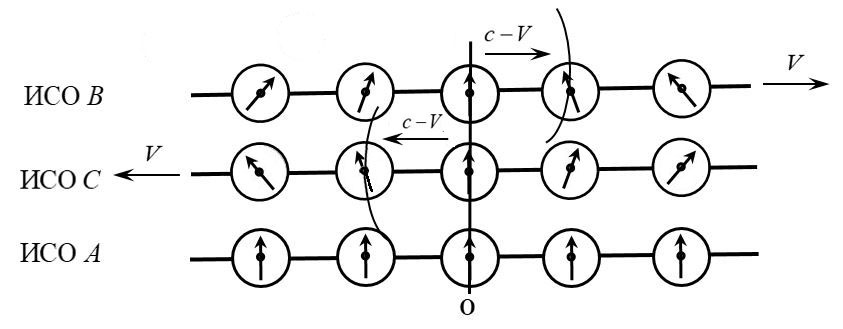
… соответствует описанию апории Зенона (Стадион), со всеми вытекающими из этой апории логическими противоречиями.

Есть еще и эксперимент Гюйгенса, когда маятники начинают молотить одинаково. В часах, особливо механических, маятники в наличии и они обречены на одинаковый ход… Правда, соговоркой — в близи друг от дружки… Такие же оговорки работают и в экскременте Кавендиша.

#73855 Evalmer :Приведенная вами схема:

… соответствует описанию апории Зенона (Стадион), со всеми вытекающими из этой апории логическими противоречиями.
Не сочиняйте. Здесь речь шла о формуле для расчета местного времени в ИСО С и ИСО В, т. е. в обеих ИСО \(t'=\gamma(t-\frac {Vx}{c^2})\) или в одной \(t'=\gamma(t-\frac {Vx}{c^2})\), а в другой \(t'=\gamma(t+\frac {Vx}{c^2})\).

Хватит пороть чушь, ибо в обеих ИСО (и В и С) имеет место быть только: \[\displaystyle t'={t-x\cdot v/c^2\over\sqrt{1-v^2/c^2}}\]… относительно ИСО А. И не надыть тута изобретати апорий. А коли вам приспичило рассматривать движение ИСО В относительно ИСО С (или сувсем даже наоборот), то будте любезны использовать релятивистский закон сложения скоростей. В вашем случае он выглядит так:
\(\displaystyle v_{(bc)}={2\cdot v\over 1+v^2/c^2}\)
отредактировал(а) Evalmer: 2026-01-09 19:31 GMT

#73933 Evalmer :Хватит пороть чушь, ибо в обеих ИСО (и В и С) имеет место быть только: \[\displaystyle t'={t-x\cdot v/c^2\over\sqrt{1-v^2/c^2}}\]… относительно ИСО А. И не надыть тута изобретати апорий. А коли вам приспичило рассматривать движение ИСО В относительно ИСО С (или сувсем даже наоборот), то будте любезны использовать релятивистский закон сложения скоростей. В вашем случае он выглядит так:
\(\displaystyle v_{(bc)}={2\cdot v\over 1+v^2/c^2}\)
А Вам известно, что отрезки собственного времени измеряются по одиночным часам?
А Вам известно, что значения собственного времени не зависят от положения (координат) в собственной ИСО?
И если решили оппонировать в этой теме, то для начала разберитесь со свойствами собственного времени, приписываемых ему в релятивистских теориях, и постарайтесь отрезки собственного времени не путать с отрезками координатного времени.





