Запутался в рассуждениях по СТО

Интервал — лоренц-инвариантная величина, то есть, от выбора системы отсчёта не зависит.
Как видите, на моём рисунке интервал AB зависит от выбора системы координат. Для одной r1^2=x1^2-t1^2 и интервал AB будет 1, для другой r2^2=x2^2-t2^2 и интервал AB=i. Что неправильно в рисунке?
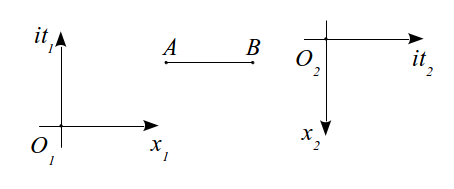
отредактировал(а) Андрей Нечитайло: 2024-05-22 10:01 GMT

#62930 Андрей Нечитайло :Они построили системы координат каждый в своей системе отсчёта.
Имеем два события: Первое — «Поезд проезжает станцию Клин в 14.00» (это 100 км от Москвы). Второе — «Поезд проезжает станцию Тверь в 14.30» (это 150 км от Москвы).
Изобразите это подобно тому, как сделали в предыдущем сообщении.
Не понял вопрос.
Довольно странно. Мой вопрос в 1000 раз понятнее вашего вопроса.
В механике Ньютона время для всех одинаковое
Разве это мешает строить зависимость перемещения от времени? Этому вроде ещё в восьмом классе учат.
, поэтому уточните, пожалуйста, что Вы называете системой координат и системой отсчета в этом случае?
Системой отсчёта и системой координат я называю во всех случаях одно и то же.
1. Тело отсчёта — это массивное тело, на котором смонтированы измерительные приборы (линейки, транспортиры, часы и всё, что может потребоваться).
(Для Алисы — это вокзал в Москве, Для Боба — это вагон поезда).
2. Система координат — метод описания состояния (изменения состояния) изучаемого явления (процесса). То есть, это способ записи (изображения) результатов измерений.
3. Система отсчета — тело отсчёта плюс система координат.
И в каком пространстве предлагаете строить?
В том же, что и вы предложили. Двумерное пространство { x — расстояние от начала системы координат, t — промежуток времени от начала координат }.
Систему координат удобно взять декартову.

#62931 Андрей Нечитайло :Интервал — лоренц-инвариантная величина, то есть, от выбора системы отсчёта не зависит.
Как видите, на моём рисунке интервал AB зависит от выбора системы координат.
Нет. Я этого не вижу. Я вижу, что на вашем рисунке изображена первая система координат и в ней два события – А и В. И затем произвольно пририсована вторая система координат.
Что неправильно в рисунке?
Всё.
Вторая система координат не может быть нарисована произвольно. Она должна быть изображена таким образом, чтобы выполнялись преобразования Галилея:
\(x^B=x^A+vt^A \\t^B=t^A\) .
Пусть в системе отсчёта Алисы есть три события: событие О \(\left ( x_O^A=0,t_O^A=0 \right )\), событие P \(\left ( x_P^A=0,t_P^A=1 \right ) \) и событие Q \(\left ( x_Q^A=1,t_Q^A=0 \right ) \). Изобразим эти события в системе координат Алисы:
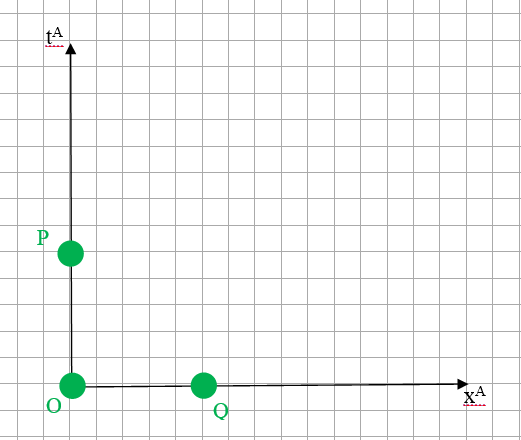
Теперь пусть Боб движется относительно Алисы со скоростью \(v=2\).
Найдём координаты событий в системе координат Боба:
\(x_O^B=x_O^A+vt_O^A = 0+2\cdot 0=0 \\t_O^B=t_O^A=0 \\x_P^B=x_P^A+vt_P^A = 0+2\cdot 1=0 \\t_O^B=t_O^A=1 \\x_Q^B=x_Q^A+vt_Q^A = 1+2\cdot 0=1 \\t_Q^B=t_Q^A=0\)
Изобразим эти события в координатах Боба:
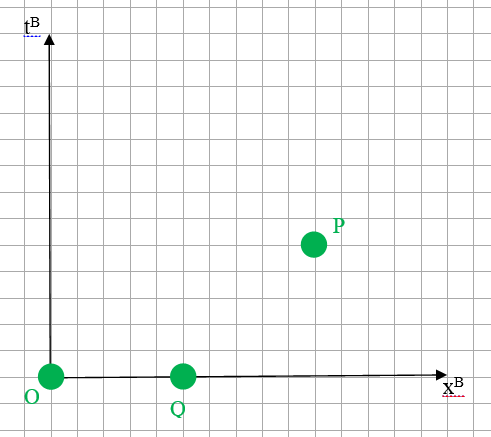
Очевидно, что никаким вращением второй картинки нельзя совместить тройку событий (зелёных кружков) с таковой на первой картинке.
А что же нужно сделать, если мы хотим обе системы координат нарисовать на одном листе? Нужно систему координат Боба сделать косоугольной. Вот так:
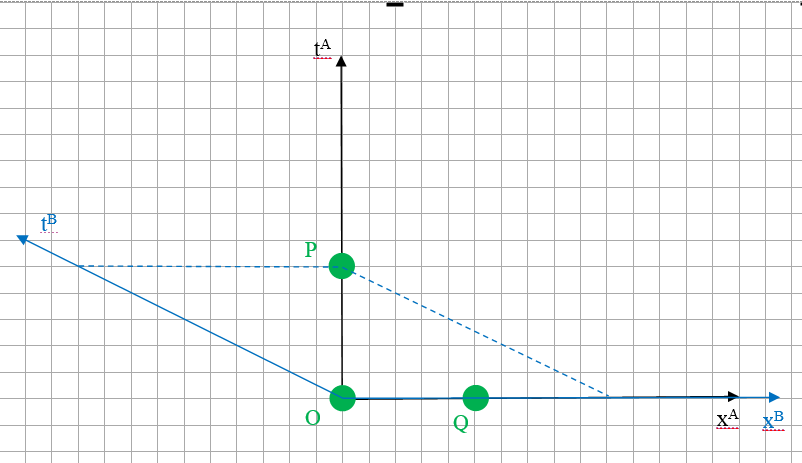
Попробуйте то же самое сделать используя преобразования Лоренца.

Вторая система координат не может быть нарисована произвольно. Она должна быть изображена таким образом, чтобы выполнялись преобразования Галилея:
При определении пространства сначала определяют скалярное произведение векторов ab=axbx+ayby у Евклида или ab=axbx-ayby у Минковского. Аксиомы одинаковые. Все остальные преобразования будут потом, в начале ещё системы координат нет. Я, возможно, неправильно понимаю и пространство Минковского не изотропное? Разные направления имеют разные свойства? Тогда в пространстве должны быть какие-то метки, которые показывают свойства направлений. Так ли?

#62953 Андрей Нечитайло :Вторая система координат не может быть нарисована произвольно. Она должна быть изображена таким образом, чтобы выполнялись преобразования Галилея:
При определении пространства сначала определяют скалярное произведение векторов ab=axbx+ayby у Евклида или ab=axbx-ayby у Минковского.
Это правильно, что метрика пространства определяется скалярным произведением. Вот только формулы вы написали чрезвычайно небрежно (строго говоря, это недопустимо). Нужно так:
Для пространства Эвклида: \(\left (\vec{a}\cdot \vec{b} \right )^2=a_xb_x+a_yb_y\) .
Для пространства Минковского: \(\left (\vec{a}\cdot \vec{b} \right )^2=a_tb_t-a_xb_x\) .
Аксиомы одинаковые.
Не совсем.
Все остальные преобразования будут потом, в начале ещё системы координат нет.
Для одного пространства можно построить сколько угодно систем координат. Ну, пускай их ещё не построили. И что? Вы хотите работать безкоординатными методами (геометрия до Декарта)?
Я, возможно, неправильно понимаю и пространство Минковского не изотропное?
Конечно не изотропное. Его свойства по разным направлениям разные. Это видно даже из метрики (скалярного произведения). Если \(a_tb_t>a_xb_x\) , то скалярное произведение векторов действительное. A если \(a_tb_t<a_xb_x\) , то скалярное произведение векторов мнимое. Или, что то же самое, если отрезок параллелен оси t, то его длина (интервал) действительна (интервал времениподобный), а если он параллелен оси x, то его длина (интервал) мнимая (интервал пространственноподобный).
Тогда в пространстве должны быть какие-то метки, которые показывают свойства направлений. Так ли?
Знак «минус» в метрике пространсмтва Минковского и является такой меткой. Из-за него пространственная координата x и временная координата t входят в метрику не симметрично.
P.S. Тут ошибки. Исправления смотрите двумя сообщениями ниже.
отредактировал(а) zam: 2024-05-23 13:46 GMT

#62954 zam :Это правильно, что метрика пространства определяется скалярным произведением. Вот только формулы вы написали чрезвычайно небрежно (строго говоря, это недопустимо). Нужно так:
Для пространства Эвклида: \(\left (\vec{a}\cdot \vec{b} \right )^2=a_xb_x+a_yb_y\) .
Для пространства Минковского: \(\left (\vec{a}\cdot \vec{b} \right )^2=a_tb_t-a_xb_x\) .
Здесь точно квадраты? Вторая степень скалярного произведения векторов? Подумайте, пожалуйста, ещё раз.

#62958 Андрей Нечитайло :#62954 zam :Это правильно, что метрика пространства определяется скалярным произведением. Вот только формулы вы написали чрезвычайно небрежно (строго говоря, это недопустимо). Нужно так:
Для пространства Эвклида: \(\left (\vec{a}\cdot \vec{b} \right )^2=a_xb_x+a_yb_y\) .
Для пространства Минковского: \(\left (\vec{a}\cdot \vec{b} \right )^2=a_tb_t-a_xb_x\) .
Здесь точно квадраты? Вторая степень скалярного произведения векторов? Подумайте, пожалуйста, ещё раз.
Вы правы. Я ошибся. Правильно так:
Для пространства Эвклида: \(\vec{a}\cdot \vec{b}=a_xb_x+a_yb_y\) .
Для пространства Минковского: \(\vec{a}\cdot \vec{b}=a_tb_t-a_xb_x\) .
Ну и, соответственно, дальше тоже нужно поправить.
Я, возможно, неправильно понимаю и пространство Минковского не изотропное?
Конечно не изотропное. Его свойства по разным направлениям разные.
Рассмотрим скалярное произведение вектора самого на себя: \(\vec{a}\cdot \vec{a}=a^2=a_t^2-a_x^2\) .
Если \(a_t^2>a_x^2\) , то длина вектора a действительная. A если \(a_t^2<a_x^2\) , то длина вектора а мнимая. Или, что то же самое, если отрезок параллелен оси t, то его длина (интервал) действительна (интервал времениподобный), а если он параллелен оси x, то его длина (интервал) мнимая (интервал пространственноподобный).

#62964 zam :Для пространства Эвклида: \(\vec{a}\cdot \vec{b}=a_xb_x+a_yb_y\) .
Для пространства Минковского: \(\vec{a}\cdot \vec{b}=a_tb_t-a_xb_x\) .
Ну и, соответственно, дальше тоже нужно поправить.
Так согласен.

#62964 zam :Конечно не изотропное. Его свойства по разным направлениям разные.
Рассмотрим скалярное произведение вектора самого на себя: \(\vec{a}\cdot \vec{a}=a^2=a_t^2-a_x^2\) .
Если \(a_t^2>a_x^2\) , то длина вектора a действительная. A если \(a_t^2<a_x^2\) , то длина вектора а мнимая. Или, что то же самое, если отрезок параллелен оси t, то его длина (интервал) действительна (интервал времениподобный), а если он параллелен оси x, то его длина (интервал) мнимая (интервал пространственноподобный).
Я уточню ещё раз. Например,
Будем называть линейным пространством множество
элементов произвольной природы, называемых
векторами, в котором определены две операции — сложение
и умножение на вещественное число, удовлетворяющие
трем группам аксиом — аксиомам сложения, аксиомам
умножения на число и аксиоме размерности. Будем
обозначать векторы, как в 1.1.3, малыми латинскими
буквами жирного шрифта.[Розенфельд Б.А. Многомерные пространства. М., 1966., стр. 20]
Пространство это набор неких объектов со свойствами и всё. Оно только что определено, осей в нём ещё нет, не выбраны, только известно, что расстояние будет определено по формуле такой-то когда они появятся. В это время в пространстве Минковского уже есть метки направлений? Чтобы не провести вещественную ось вдоль мнимого направления.

#62966 Андрей Нечитайло :Будем называть линейным пространством множество
элементов произвольной природы, называемых
векторами, в котором определены две операции — сложение
и умножение на вещественное число, удовлетворяющие
трем группам аксиом — аксиомам сложения, аксиомам
умножения на число и аксиоме размерности. Будем
обозначать векторы, как в 1.1.3, малыми латинскими
буквами жирного шрифта.[Розенфельд Б.А. Многомерные пространства. М., 1966., стр. 20]
Пространство это набор неких объектов со свойствами и всё.
Да, конечно. И эти объекты называются векторами. (Тут речь идёт про метрические векторные пространства; про другие пространства, например, топологические, я имею весьма смутные представления).
А определение Розенфельда почти идеально. Меня там только смущает слово «линейным». Обычно в этом месте пишут «векторным».
Оно только что определено, осей в нём ещё нет, не выбраны, только известно, что расстояние будет определено по формуле такой-то когда они появятся.
В это время в пространстве Минковского уже есть метки направлений?
В пространстве нет ничего, кроме векторов (пространство состоит из векторов). Метки (точнее метка) — она в формуле, определяющей метрику пространства.
Чтобы не провести вещественную ось вдоль мнимого направления.
Ось вы проводите не в пространстве, а на листе бумаги. И даёте её название, таким образом привязывая к метрике.
И такие словосочетания, как «вещественная ось», «мнимое направление» нуждаются в пояснении (определении).

#62977 zam :В пространстве нет ничего, кроме векторов (пространство состоит из векторов). Метки (точнее метка) — она в формуле, определяющей метрику пространства.
Точки на листе бумаги соответствуют точкам пространства и обратно, иначе лист бумаги, как геометрическая модель пространства, не работал бы — нельзя было бы условия задачи из пространства перенести на бумагу и выводы, полученные на бумаге перенести обратно в пространство. Когда я на бумаге провожу прямую, я в неё включаю выбранные мной точки и бумаги и соответствующие им точки пространства.
Если в самом пространстве нет меток, тогда не понятно по каким признакам Вы выбираете точки пространства, чтобы включить их в каждую из осей координат. По каким признакам Вы узнаёте по какому из направлений пространства интервалы вещественные, а по какому направлению они мнимые, когда осей ещё нет?

#62978 Андрей Нечитайло :#62977 zam :В пространстве нет ничего, кроме векторов (пространство состоит из векторов). Метки (точнее метка) — она в формуле, определяющей метрику пространства.
Точки на листе бумаги соответствуют точкам пространства и обратно, иначе лист бумаги, как геометрическая модель пространства,
Я бы сказал наоборот. Пространство — это модель того, что вы рисуете на листе бумаги.
Более строго. Пространство (в узком смысле) — это математическая модель, предназначеная для упорядочения результатов измерений расстояний и углов.
нельзя было бы условия задачи из пространства перенести на бумагу и выводы, полученные на бумаге перенести обратно в пространство.
Такое впечатление, что вы считаете пространство чем-то реально существующим, материальным.
А это чистая абстракция. Как число. Как функция. Как энергия.
Когда я на бумаге провожу прямую, я в неё включаю выбранные мной точки и бумаги и соответствующие им точки пространства.
Вы изображаете на листе бумаги результаты эксперимента (реального или мысленного).
Если в самом пространстве нет меток, тогда не понятно по каким признакам Вы выбираете точки пространства, чтобы включить их в каждую из осей координат.
Да не выбираю я никаких точек! Я беру результат измерения (линейкой и часами) и отмечаю его точкой в декартовой системе координат.
По каким признакам Вы узнаёте по какому из направлений пространства интервалы вещественные, а по какому направлению они мнимые, когда осей ещё нет?
По результатам расчёта. Имеется пара событий.(x1, t1) и .(x2, t2) . Квадрат интервала между этими событиями \(s^2=(t_1-t_2)^2-(x_1-t_2)^2\) . Если \(s^2>0\) , то интервал действительный, иначе мнимый. Для этого расчёта мне никакие оси не нужны.

#62986 zam :
Да не выбираю я никаких точек! Я беру результат измерения (линейкой и часами) и отмечаю его точкой в декартовой системе координат.
Систему координат на листе Вы выбираете произвольно, как сами решаете? И уже от расположения осей зависит где интервалы реальные, а где мнимые?

#62993 Андрей Нечитайло :#62986 zam :Да не выбираю я никаких точек! Я беру результат измерения (линейкой и часами) и отмечаю его точкой в декартовой системе координат.Систему координат на листе Вы выбираете произвольно, как сами решаете?
Конечно. Как мне удобно, так и рисую. Чаще всего прямоугольную декартову.
И уже от расположения осей зависит где интервалы реальные, а где мнимые?
Это зависит от координат событий. Изображённые отрезки будут соответствовать действительным интервалам, если они составляют с осью времени угол меньше 450. А если больше, то интервал мнимый.

#63001 zam :Конечно. Как мне удобно, так и рисую. Чаще всего прямоугольную декартову...
Изображённые отрезки будут соответствовать действительным интервалам, если они составляют с осью времени угол меньше 450. А если больше, то интервал мнимый.
То есть, из множества векторов, составляющих линейное пространство М листа бумаги, Вы выбираете некоторые и включаете их в подмножество x1, их конечные точки изобразят ось координат x1. Так же выбираете подмножество t1 и ещё будет одна точка, входящая одновременно в оба подмножества - точка начала координат O1. От выбора этих подмножеств зависят расстояния между точками множества M по формуле \(r_1 ^2=x_1 ^2-t_1 ^2\). Но ведь никто не помешает мне включить другие векторы из М в другие подмножества x2 и t2 с их пересечением в O2, так я назначу другую систему координат и другие расстояния между точками М. Тогда см. рис. Расстояние AB будет одновременно равно и 1 и i.
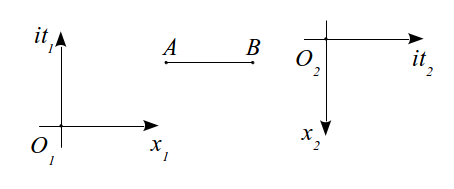
В нашем пространстве Евклида тоже никто не помешает на одном листе выбрать несколько систем координат, но таких коллизий не предвидится, все длины будут найдены равными (с точностью до длины единичного вектора) во всех системах по теореме Пифагора.

#63022 Андрей Нечитайло :#63001 zam :Конечно. Как мне удобно, так и рисую. Чаще всего прямоугольную декартову...
Изображённые отрезки будут соответствовать действительным интервалам, если они составляют с осью времени угол меньше 450. А если больше, то интервал мнимый.То есть, из множества векторов, составляющих линейное пространство М листа бумаги, Вы выбираете некоторые и включаете их в подмножество x1, их конечные точки изобразят ось координат x1.
Давайте не спеша, аккуратно, разберём эту процедуру.
Имеется лист бумаги. Точки его поверхности образуют линейное пространство. Я нарисовал на листе две линии, назвал их «x» и «t». И отметил на них единичные отрезки. Тем самым я каждой (какой захочу) точке листа бумаги поставил в соответствие пару чисел: точка А = (tА, xA):
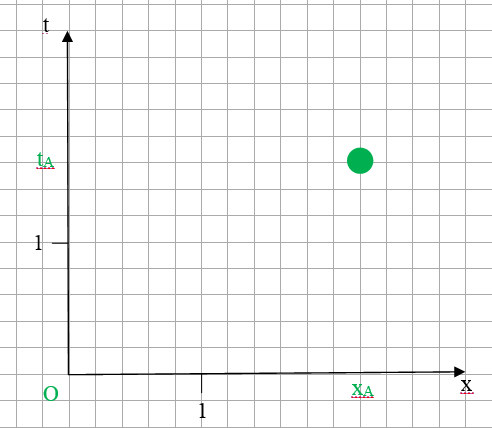
Далее. Кроме пространства листа бумаги у меня есть усечённое пространство Минковского (усечённое — потому что я не обращаю внимания на координаты y и z). То есть, множество событий (t, x), то есть, множество результатов измерений, полученных приборами некоторой ИСО (часами и линейками). И я ставлю во взаимно однозначное соответствие множество точек листа и множество событий пространства Минковского. Получается, что точке «A» соответствует событие (1.6 секунды, 2.2 световых секунды).
Но ведь никто не помешает мне включить другие векторы из М в другие подмножества x2 и t2 с их пересечением в O2, так я назначу другую систему координат и другие расстояния между точками М.
Никто не помешает. Кроме того, что в ваших новых координатах (t2, x2) координаты точки А должны быть либо теми же самыми (а это значит, что вторая система координат полностью совпадает с первой), либо удовлетворять преобразованиям Лоренца (переход в другую ИСО), и тогда они будут косоугольными и повёрнутыми на угол, зависящий от того, с какой скоростью вторая ИСО движется относительно первой.
Получится нечто вот такое:
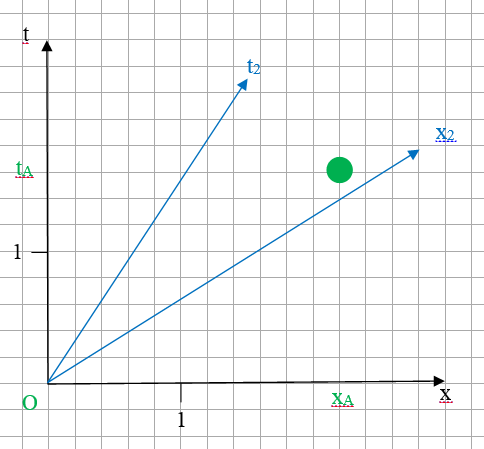
В нашем пространстве Евклида тоже никто не помешает на одном листе выбрать несколько систем координат, но таких коллизий не предвидится, все длины будут найдены равными (с точностью до длины единичного вектора) во всех системах по теореме Пифагора.
Всё верно. А причина этого в том, что в пространстве Эвклида координаты x и y равноправны (от их перестановки не изменяется ничего): \(\Delta s^2=\Delta x^2+\Delta y^2=\Delta y^2+\Delta x^2\) .
А в пространстве Минковского не так: \(\Delta s^2=\Delta t^2-\Delta x^2\neq \Delta x^2-\Delta t^2\) .
Если в пространстве Эвклида поворот системы координат описывается матрицей из синусов и косинусов от угла поворота, то в пространстве Минковского поворот системы координат описывается матрицей из гиперболических синусов и гиперболических косинусов от угла поворота.

Я имею в виду, что, прежде чем задавать соответствие точек листа мировым событиям и вводить дополнительные ограничения преобразованиями Лоренца, надо построить на листе систему координат. Вы строите свою, я свою и Лоренцевы преобразования ещё не введены, потому что точки листа ещё не мировые события, а только точки с формулой нахождения расстояния \(r_A^2=x_A^2-t_A^2\), других формул пока нет, ведь ПМ не обязательно использовать только для ТО, его определяют в учебниках (да хоть у Розенфельда) само по себе, без Лоренца. И в этом случае получится мой рисунок и пространство Минковского приведет к \(i=1\). Уже само по себе оно противоречиво.

#63085 Андрей Нечитайло :Я имею в виду, что, прежде чем задавать соответствие точек листа мировым событиям и вводить дополнительные ограничения преобразованиями Лоренца, надо построить на листе систему координат.
Так и сделано.
Вы строите свою, я свою
Вот и стройте её на своём листе бумаги.
и Лоренцевы преобразования ещё не введены,
Они введены ещё до того, как мы стали что-то рисовать. Кат только мы сказали, что собираемся рисовать координаты для изображения пространства Минковского, тут же преобразования Лоренца и появились.
потому что точки листа ещё не мировые события,
Как только мы подписали оси координат и отметили на них единичный масштаб, тут же точки листа стали изображениями событий.
а только точки с формулой нахождения расстояния \(r_A^2=x_A^2-t_A^2\), других формул пока нет,
Так эта формула (метрика) — прямое следствие преобразований Лоренца. Или наоборот из этой метрики выводятся преобразования Лоренца.
ведь ПМ не обязательно использовать только для ТО,
А где ещё? Я других приложений не встречал.
его определяют в учебниках (да хоть у Розенфельда) само по себе, без Лоренца.
В каком учебнике? «Неевклидовы геометрии»? Там про приложения ничего нет. Только определение.
И в этом случае получится мой рисунок и пространство Минковского приведет к \(i=1\).
Вы не можете на моём листе рисовать свои координаты произвольно. Можете только так, чтобы соблюдались закономерности пространства Минковского.
Уже само по себе оно противоречиво.
Никаких противоречий пространство Минковского не содержит. Оно ровно настолько непротиворечиво, насколько непротиворечиво пространство Евклида (или Лобачевского, или Римана...).
отредактировал(а) zam: 2024-05-30 09:44 GMT

«Релятивистская масса» — это бесполезный (и даже вредный) термин, появившийся на начальных этапах развития СТО. результат довольно бессмысленной попытки сохранить привычные выражения для кинетической энергии и импульса.
Пользуясь случаем, хотел спросить. Что создает гравитацию (градиент в гравитационном поле, гравитационную силу притяжения, как правильно говорить?), масса покоя или релятивистская масса?
Попробую пояснить вопрос. Если луч света летит мимо массивного объекта, то он изгибается в сторону этого объекта. Я, как обыватель, делаю вывод, что фотоны, обладая релятивистской массой, испытывают гравитационное притяжение. Если посмотреть на эту ситуацию наоборот и лучом светить рядом с объектом, обладающим массой, создаст ли луч градиент в гравитационном поле? Начнет ли объект притягиваться к лучу?
Не сочтите за оффтопик, мне правда интересно.


#63127 Константин-2 :«Релятивистская масса» — это бесполезный (и даже вредный) термин, появившийся на начальных этапах развития СТО. результат довольно бессмысленной попытки сохранить привычные выражения для кинетической энергии и импульса.Что создает гравитацию (градиент в гравитационном поле, гравитационную силу притяжения, как правильно говорить?),
Лучше так: «что создаёт гравитационное поле» или «что является источником гравитационного поля».
масса покоя или релятивистская масса?
Не то и не другое. (Чем раньше вы забудете термины «масса покоя» и «релятивистская масса», тем лучше).
Как видно из основного уравнения ОТО (уравнения Эйнштейна-Гильберта)

источником гравитационного поля является правая часть уравнения, \( T_{\mu \nu} \). Это симметричный тензор второго ранга, тензор энергии-импульса. Он имеет 10 независимых компонент:
— плотность энергии — 1 число;
— вектор плотности потока энергии (вектор Пойнтинга) — 3 числа;
— вектор плотности импульса — 3 числа;
— вектор плотности потока импульса — 3 числа.
В связи с этим иногда говорят, что у гравитации 10 зарядов (10 перечисленных чилел). Но я не сторонник такого выражения.
Попробую пояснить вопрос. Если луч света летит мимо массивного объекта, то он изгибается в сторону этого объекта.
Да.
Я, как обыватель, делаю вывод, что фотоны, обладая релятивистской массой, испытывают гравитационное притяжение.
Фотоны испытывают гравитационное притяжение по той причине, что обладают энергией и импульсом.
Если посмотреть на эту ситуацию наоборот и лучом светить рядом с объектом, обладающим массой, создаст ли луч градиент в гравитационном поле?
Создаст.
Любой объект, обладающий энергией и импульсом (то есть вообще любой объект) создаёт гравитационное поле. Гравитационное взаимодействие — универсально, в нём участвует всё.
Начнет ли объект притягиваться к лучу?
Раз луч света притягивается к Солнцу, то и Солнце притягивается к лучу. Закон сохранения импульса никто не отменял.
И два луча света притягиваются один к другому. Но настолько слабо, что нет никакой надежды это измерить.
Не сочтите за оффтопик, мне правда интересно.
Никаких признаков оффтопика.

#62189 zam :#62148 skv001 :#62121 zamЕсли Алиса и Боб сообразительны, то они сформулируют закон таким образом: «Результат измерения углового размера объекта зависит от расстояния между объектом и измерительным прибором; чем больше расстояние, тем меньше угловой размер.
Тогда они могли бы сообразить, что результаты измерений с помощью нестабильных линеек и часов
У них стабильные линейки и часы.
Ведь если линейка укорачивается при движении относительно физического вакуума,
Она не укорачивается.
А поскольку при движении часов замедляется их ход
Он не замедляется.
Это и создаёт иллюзию постоянства скорости света и равноправия всех инерциальных систем отсчёта.
Это не иллюзии.
Уже обнаружены признаки влияния абсолютной скорости Земли на многие процессы
У Земли нет абсолютной скорости.
привязать к реликтовому излучению, по асимметрии которого уже определили абсолютную скорость Земли.
Не абсолютную скорость Земли, а относительную скорость Земли. Скорость Земли относительно реликтового фона.
Законы N2 и N3 это всем известная теория относительности.
Законы №2 и №3 — это галиматья.
Теория относительности известна очень многом, но вы в их число не входите.
Она почти работает и годится для решения простейших задач.
Не известно ни одного явления, ни одного эксперимента, где бы теория относительности не работала.
Но вы правы, теория относительности глупость,
Я прав в том, что вы глупы.
Хамство и враньё буду удалять. Предупреждаю. Тем более, это тематический раздел.
Вы же не сплющиваетесь от того, что где-то в дальнем космосе кто-то летит со скоростью 0.8с относительно вас?
Согласно теории относительности, я реально сплющиваюсь в другой вселенной, в которой неподвижен этот космонавт.
Враньё. Перестаньте рассуждать о том, в чём не разбираетесь.
Не размер тела космонавта „становится“, а результат измерения этого размера „становится“.
Вы хотите сказать, что движущееся линейка только кажется укороченной?
Я говорь вот как: Результат измерения длины движущейся линейки будет меньше, чем результат измерения покоящейся линейки.
С длинами линейки нет ошибки? Если длина линейки L = Vt, то с точки зрения наблюдателя «А», мимо которого пролетает линейка, при стремлении скорости линейки (V) к скорости света, время t будет стремиться к бесконечности, т.к. \(t = {tл. \over\sqrt{1-(V^2/c^2)} }\), где tл. это время в СО линейки. Знаменатель стремится к нулю, соответственно t стремится к бесконечности, и L линейки тоже стремится к бесконечности.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2024-06-03 15:27 GMT

#63252 Valery Z :#62189 zam :Я говорь вот как: Результат измерения длины движущейся линейки будет меньше, чем результат измерения покоящейся линейки.
С длинами линейки нет ошибки?
Нет.
Если длина линейки L = Vt,
Что такое V? Что такое t?
то с точки зрения наблюдателя «А», мимо которого пролетает линейка, при стремлении скорости линейки (V) к скорости света, время t будет стремиться к бесконечности, т.к. \(t = {tл. \over\sqrt{1-(V^2/c^2)} }\), где tл. это время в СО линейки. Знаменатель стремится к нулю, соответственно t стремится к бесконечности, и L линейки тоже стремится к бесконечности.
Вы что-то невразумительное написали. Попробуйте из учебника переписать, что-ли.
Если мимо наблюдателя со скоросью v пролетает линейка, собственная длина которой равна L, то результат измерения длины лнейки этим наблюдателем будет равен
\(L'=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\) .
P.S. Прошу прощения. Формулу я написал неправильно. Нужно так: \(L'=L\sqrt{1-\frac{v^2}{c^2}}\) .
отредактировал(а) zam: 2025-03-13 21:50 GMT

#63100 zam :
Вот и стройте её на своём листе бумаги.
Это ещё почему? Разве построение системы координат не произвольно?

#63291 zam :#63252 Valery Z :#62189 zam :Я говорь вот как: Результат измерения длины движущейся линейки будет меньше, чем результат измерения покоящейся линейки.
С длинами линейки нет ошибки?
Нет.
Если длина линейки L = Vt,
Что такое V? Что такое t?
то с точки зрения наблюдателя «А», мимо которого пролетает линейка, при стремлении скорости линейки (V) к скорости света, время t будет стремиться к бесконечности, т.к. \(t = {tл. \over\sqrt{1-(V^2/c^2)} }\), где tл. это время в СО линейки. Знаменатель стремится к нулю, соответственно t стремится к бесконечности, и L линейки тоже стремится к бесконечности.
Вы что-то невразумительное написали. Попробуйте из учебника переписать, что-ли.
Если мимо наблюдателя со скоросью v пролетает линейка, собственная длина которой равна L, то результат измерения длины лнейки этим наблюдателем будет равен
\(L'=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\) .
Как наблюдатель будет измерять длину линейки? Наверное, зная её скорость и время, которое прошло между фиксациями начала и конца линейки. Хорошо, пусть в формуле будет длина L. Но знаменатель всё равно стремится к нулю при V стремящемся к скорости света. Соответственно, результат измерения длины линейки должен стремиться к бесконечности.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2024-06-02 21:40 GMT


#63291 zam :#63252 Valery Z :#62189 zam :Я говорь вот как: Результат измерения длины движущейся линейки будет меньше, чем результат измерения покоящейся линейки.
С длинами линейки нет ошибки?
Нет.
Если длина линейки L = Vt,
Что такое V? Что такое t?
то с точки зрения наблюдателя «А», мимо которого пролетает линейка, при стремлении скорости линейки (V) к скорости света, время t будет стремиться к бесконечности, т.к. \(t = {tл. \over\sqrt{1-(V^2/c^2)} }\), где tл. это время в СО линейки. Знаменатель стремится к нулю, соответственно t стремится к бесконечности, и L линейки тоже стремится к бесконечности.
Вы что-то невразумительное написали. Попробуйте из учебника переписать, что-ли.
Если мимо наблюдателя со скоросью v пролетает линейка, собственная длина которой равна L, то результат измерения длины лнейки этим наблюдателем будет равен
\(L'=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\) .
Если мимо лнейки, собственная длина которой равна L, пролетает со скоросью v наблюдатель, то результат измерения длины лнейки этим наблюдателем будет равен
\(L'=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\) .
P.S. Прошу прощения. Формулу я написал неправильно. Нужно так: \(L'=L\sqrt{1-\frac{v^2}{c^2}}\) .
Крайняя Ваша формула показывает, какую длину линейки видит наблюдатель «А» с точки зрения наблюдателя, находящегося в СО линейки? Но Вы говорите о результате измерения длины «движущейся» линейки, — то, что он (результат) будет меньше, чем — покоящейся линейки.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков

#63293 Valery Z :#63291 zam :\(L'=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\) .
Как наблюдатель будет измерять длину линейки? Наверное, зная её скорость и время, которое прошло между фиксациями начала и конца линейки.
Можно и так. \(L'=v \Delta t'\) .
Хорошо, пусть в формуле будет длина L. Но знаменатель всё равно стремится к нулю при V стремящемся к скорости света. Соответственно, результат измерения длины линейки должен стремиться к бесконечности.
Я ошибся в записи формулы (уже поправил).
Правильно так: \(L'=L\sqrt{1-\frac{v^2}{c^2}}\) .
Результат измерения длины стремится к нулю. Это называется сокращением Лоренца-Фицджеральда.

#63301 zam :#63293 Valery Z :#63291 zam :\(L'=\frac{L}{\sqrt{1-\frac{v^2}{c^2}}}\) .
Как наблюдатель будет измерять длину линейки? Наверное, зная её скорость и время, которое прошло между фиксациями начала и конца линейки.
Можно и так. \(L'=v \Delta t'\) .
Хорошо, пусть в формуле будет длина L. Но знаменатель всё равно стремится к нулю при V стремящемся к скорости света. Соответственно, результат измерения длины линейки должен стремиться к бесконечности.
Я ошибся в записи формулы (уже поправил).
Правильно так: \(L'=L\sqrt{1-\frac{v^2}{c^2}}\) .
Результат измерения длины стремится к нулю. Это называется сокращением Лоренца-Фицджеральда.
Вопрос: — какой способ измерения подразумевается в данном случае? Если «ощущениями» наблюдателя это одно, а если приборами, то – другое. Допустим, наблюдатель включил лазерный луч перпендикулярно направлению движения линейки, и ждёт, когда передний конец летящей линейки наскочит на этот луч. Когда это событие произошло, луч отразился от линейки и попал на фотоэлемент прибора (хронометра) – время пошло. Когда линейка закончилась, фотоэлемент выключил хронометр. Данный промежуток времени будет ∆t´, и он по логике (при вышеописанном способе измерения) должен соответствовать собственной длине линейки при скорости V. Если \(∆t´=\frac{∆t}{\sqrt{1-\frac{v^2}{c^2}}}\) , где ∆t – это промежуток времени с позиции наблюдателя, находящегося в СО линейки, то ∆t´в данном случае, будет стремиться к бесконечности, а L´(по сокращению Лоренца) - к нулю. Получается противоречие. Где ошибка?
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2024-06-03 20:06 GMT

#63323 Valery Z :#63301 zam :Правильно так: \(L'=L\sqrt{1-\frac{v^2}{c^2}}\) .
Результат измерения длины стремится к нулю. Это называется сокращением Лоренца-Фицджеральда.
Вопрос: — какой способ измерения подразумевается в данном случае?
Какой угодно.
Если «ощущениями» наблюдателя это одно, а если приборами, то – другое.
Одно и то же. Приборы — это усилители (уточнители) органов чувств.
Допустим, наблюдатель включил лазерный луч перпендикулярно направлению движения линейки, и ждёт, когда передний конец летящей линейки наскочит на этот луч. Когда это событие произошло, луч отразился от линейки и попал на фотоэлемент прибора (хронометра) – время пошло. Когда линейка закончилась, фотоэлемент выключил хронометр.Фок в своём учебнке по еорям оносельнос.
Очень хорошо. Такой способ измерений называется радиолокационным. Именно такой способ использовал Владимир Фок в своём учебнике по теориям относительности.
Данный промежуток времени будет ∆ t´,
∆ t´ — это промежуток времени, насчитанный хронометром? То есть, штрихами вы помечаете величины в системе отсчёта наблюдателя?
и он по логике (при вышеописанном способе измерения) должен соответствовать собственной длине линейки при скорости V.
Нет. Он будет равен ∆ t´ = L'/v, где L' — результат измерения длины линейки в системе наблюдателя, v — скорость линейки относительно наблюдателя.
\(L'=L_0\sqrt{1-\frac{v^2}{c^2}}\). Здесь L0 — собственная длина линейки. Поэтому \(\Delta t'=\frac{L'}{v}=\frac{L_0}{v}\sqrt{1-\frac{v^2}{c^2}}\) .
Если \(∆t´=\frac{∆t}{\sqrt{1-\frac{v^2}{c^2}}}\) , где ∆t – это промежуток времени с позиции наблюдателя, находящегося в СО линейки,
Не так. ∆t´ — это промежуток времени между включением и выключением хронометра в системе наблюдателя. Промежуток времени между этими событиями в системе отсчёта линейки будет равен \(\Delta t=\frac{\Delta t'}{\sqrt{1-\frac{v^2}{c^2}}}\) .
то ∆ t ´в данном случае, будет стремиться к бесконечности,
При \(v\rightarrow c\) ∆t´ стремится к нулю.
а L ´(по сокращению Лоренца) - к нулю.
При \(v\rightarrow c\) L´ стремится к нулю.
П олучается противоречие.
Никаких противоречий.
Где ошибка?
Ваша ошибка в том, что вы не определяете строго, какие величины к каким системам отсчёта относятся. и механически применяете формулы из учебников не задумываясь о том, как их следует применять в конкретной задаче.
отредактировал(а) zam: 2024-06-10 21:16 GMT





