Циклические цепочки

В работе представлены полные аналитические решения для циклически замкнутой цепочки произвольного числа упруго связанных тел, т.е. для случая, когда граничные условия записать принципиально невозможно в силу отсутствия самой границы.
В периодическом режиме колебания имеют вид

Для апериодического режима:

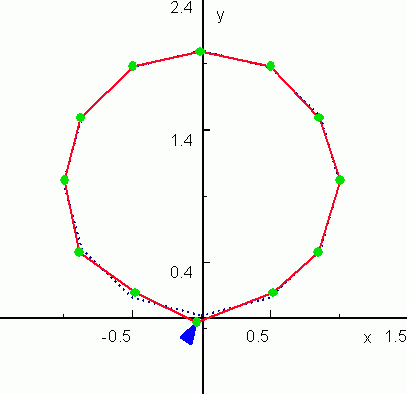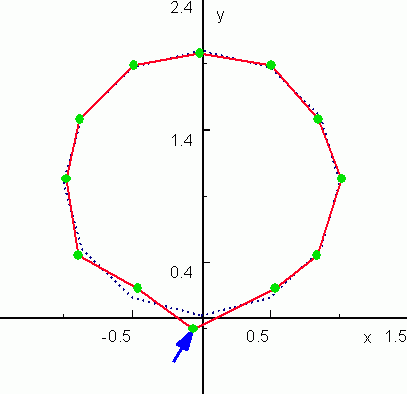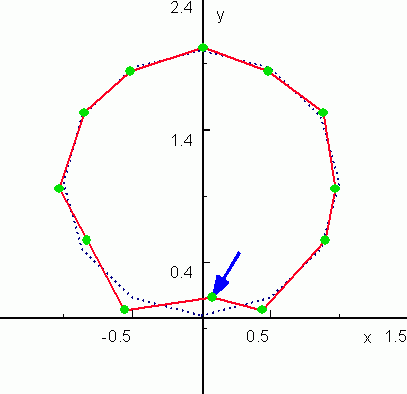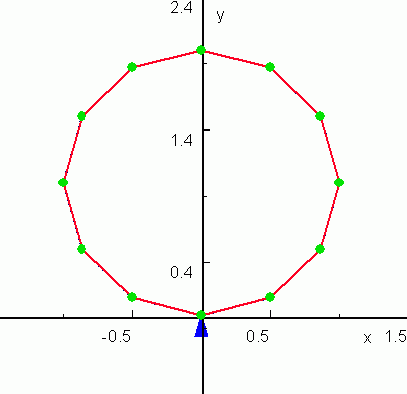
Реакция цепочки на распределенную вдоль цепочки гармоническую внешнюю силу в периодическом режиме:

«здесь уже нет однозначного соответствия между направлением действующей на каждую массу силы и направлением отклонения данной массы от состояния равновесия. Начинают проявляться особенности наложения колебаний, распространяющихся в самой цепочке, которые геометрически налагаются на внешнее воздействие, но зависят от комплекса реакции системы на все её массы. С этим и связан эффект движения отдельных масс цепочки встречно направлению силы, воздействующей на них.
Данный режим возникает при росте скорости транспортного средства и, понятно, в случае покрышки является значительно более жёстким режимом, напрягающим её корд. К тому же, из-за встречного движения внешней воздействующей силы и массы, на которую происходит воздействие, будет увеличиваться стирающее усилие покрышки, а значит, ускоряться её износ. С этой точки зрения, для транспортных средств, обладающих большими нагрузками на покрышки и большими скоростями, необходимо, чтобы система не переходилв в апериодический режим,

который для цепочки является значительно более напряжённым из-за локальных напряжений между элементами.
В случае же неравенства продольной и поперечной жёсткости на изменении направления цепочки появляется узкий излом,
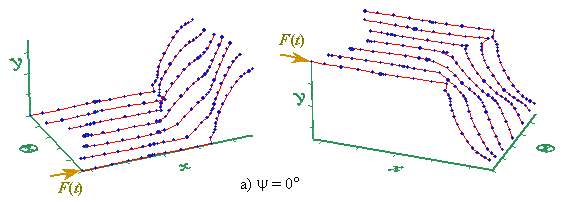

Влияние излома на картину колебательного процесса в линии усугубляет процесс.
http://selftrans.narod.ru/v2_1/bend/bend097/bend097rus.html
Таким образом, точные аналитические решения позволяют существенно уточнить картину колебмтельного процесса в циклических цепочках и открывают дорогу для построения точных аналитических решений на двумерных структурах.

В антенной технике тоже есть цепочки, одно зависит от другого и в конце замыкается, но принято некоторое допущение и в итоге находится решение. К примеру программа MANA. Или Microwave Office
Механические рассчеты с небольшими упрощениями можно сделатьв SolidWorks, более сложно в ANSYS.
Мне кажется (мое сугубо личное мнение) системы с обратной связью все расчитываются с некоторыми упрощениям.
Механики не изучают электрические системы с обратной связью, передачточные функции и четырехполюсники, а электронщики не изучают нелинейные механические системы в динамике, поэтому общего понимания пока не существует.

#50447 givigudze :В антенной технике тоже есть цепочки, одно зависит от другого и в конце замыкается, но принято некоторое допущение и в итоге находится решение. К примеру программа MANA. Или Microwave Office
Механические рассчеты с небольшими упрощениями можно сделатьв SolidWorks, более сложно в ANSYS.
Мне кажется (мое сугубо личное мнение) системы с обратной связью все расчитываются с некоторыми упрощениям.
Механики не изучают электрические системы с обратной связью, передачточные функции и четырехполюсники, а электронщики не изучают нелинейные механические системы в динамике, поэтому общего понимания пока не существует
Обманывать себя легко, но эти решения получить существующими методами невозможно. :-)




