Найти высоту свободного падения тела, не банально!

Прошу помочь с решением такой задачи: Камень весом 1,5-2(кг) уронили в колодец, глубокий. Очень глубокий. Он пролетел «t» секунд и шлепнулся в воду.
Поскольку колодец «очень глубокий», то во времени «t» надо учитывать как время свободного падения камня «t1», так и время возврата звука назад «t2», по сумме которых зафиксировано окончание измерения общего времени. Без учета времени возврата звука «t2» получил высоту что-то около 1860м.
Значит, что мы имеем:
h — высота, искомая величина; t1 — время свободного падения камня с высоты h; t2 — время возврата звука на расстоянии h; Сопротивлением воздуха пренебрегаем; ускорение g = 9.8м/с2; скорость звука в воздухе при температуре (20гр.Ц) примем Vзв. = 340м/с, начальная скорость падения тела V0 = 0;
t = t1+t2 = 19.5 (cек.)
t1>>t2
h(высота) = (g*t12)/2 = Vзв. * t22
\(t1 + t2 = \sqrt {2h \over g} + {h \over Vзв.}\)
с учетом преобразований системы уравнений получил равенство:
t2 = (2 * Vзв2 * h + gh2)/(g * Vзв2), или: \(t^2 = {2 * Vзв^2 * h + g * h^2 \over g * Vзв^2}\)
Приехали… Что делать дальше — ума не приложу, Может где ошибся — проверял, ошибок не нашел.
Проблема в том, что искомая величина «h» содержится в одной части уравнения в разных степенях — t2 = (2 * Vзв2 * h + gh2)/(g * Vзв2).
Как это дело привести к виду «h = ...» я не знаю. Но ведь должно быть какое-то решение...

Подозреваю, что при преобразованиях я неправильно возвел в степень двучлен \((\sqrt {2h \over g} + {h \over Vзв.})\)...
Хотя от этого не легче — h в разных степенях присутствует в начальной системе уравнений, см. выше...
отредактировал(а) Barmaley: 2020-10-09 20:36 GMT
#39250 Barmaley :Прошу помочь с решением такой задачи: Камень весом 1,5-2(кг) уронили в колодец, глубокий. Очень глубокий. Он пролетел «t» секунд и шлепнулся в воду.
Поскольку колодец «очень глубокий», то во времени «t» надо учитывать как время свободного падения камня «t1», так и время возврата звука назад «t2», по сумме которых зафиксировано окончание измерения общего времени. Без учета времени возврата звука «t2» получил высоту что-то около 1860м.
Значит, что мы имеем:
h — высота, искомая величина; t1 — время свободного падения камня с высоты h; t2 — время возврата звука на расстоянии h; Сопротивлением воздуха пренебрегаем; ускорение g = 9.8м/с2; скорость звука в воздухе при температуре (20гр.Ц) примем Vзв. = 340м/с, начальная скорость падения тела V0 = 0;
t = t1+t2 = 19.5 (cек.)
Откуда числа?
В условии никаких чисел НЕТ.
Не путай людей.
«Целкни кобылу в нос — она взмахнет хвостом.»
«Зри в корень» К.Прутков С
Я умею читать мысли других, но только тогда, когда они у них есть

не понял, какие «числа», о чем вы?
Кстати, я неправильно равенство записал в спешке:
h(высота) = (g*t12)/2 = Vзв. * t22 — квадрат лишний!
Правильно: h(высота) = (g*t12)/2 = Vзв. * t2.
П.С.
Интересно ее решить с учетом сопротивления воздуха, если принять, что камень — это шар с диаметром 10(см), и массой 1,5(кг).

Ваша задача элементарно решается если нарисовать график
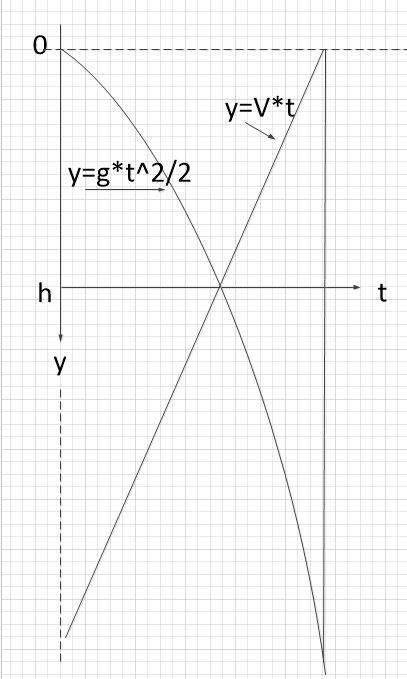
\(h=g\frac{t_1^2}{2}\)
\(h=Vt_2\)
\(t_1+t_2=19.5\)
отредактировал(а) Очепятка: 2020-10-10 18:40 GMT

\(t_2=\frac{g}{2V}t_1^2\)
Введем переменную для упрощения записи
\(a=\frac{g}{2V}\)
\(t_1+at_1^2=19.5\)
Очевидно квадратное уравнение
\(at_1^2+bt_1+c=0\)
\(b=1\)
\(c=-19.5\)
\(t_1=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\)
Отрицательное время физического смысла не имеет выкидываем его и делаем обратную замену
\(t_1=\frac{V\left({-1 + \sqrt{1-2\cdot 19.5\cdot \frac{g}{V}}}\right)}{g}\)
\(h=(19.5-t_1)V\)
отредактировал(а) Очепятка: 2020-10-10 18:52 GMT

\(t_1=15.87\)
\(h=1234\)
отредактировал(а) Очепятка: 2020-10-10 18:44 GMT

Благодарю вас за лаконичный и законченный ответ. Плюсик ушел.
![]()




