Работа перемещения заряда в электрическом поле

Бесконечно большая равномерно заряженная плоскость и параллельная ей длинная нить расположены как показано на рисунке (перпендикулярно плоскости чертежа); а = 20 см; поверхностная плотность заряда плоскости 10^-6 Кл/м²; линейная плотность заряда нити 10^-6 Кл/м.

Определить: напряжённость поля в точках А и В; работу перемещения заряда 10^-7 Кл из точки А в точку В. Считать, что распределение зарядов не нарушено взаимодействием.

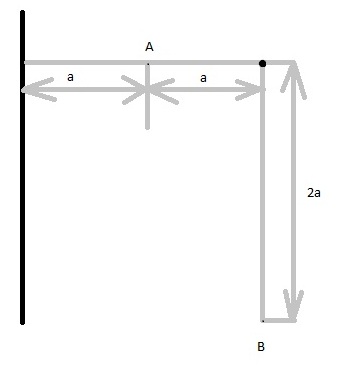
Здравствуйте! Помогите пожалуйста с решением задачи. Правильно ли я понимаю, что чёрная линия и жирная чёрная точка это те самые плоскость и линия, и направлены они от нас? Истолковав так чертёж, я нашёл напряжённости в точках А и В:

вектор Е_А = вектор Е_{пл. А} + вектор Е_{л. А}

Е_А = |Е_{пл. А} - Е_{л. А}|

Для нахождения напряжённостей эл. поля плоскости и линии использую формулы:

Е_пл. = поверх. плотн. зар./(2*эл. постоянная), где эл. постоянная = 8,854*10^-12

Е_л. = лин. плотн. зар./(2П*эл. постоянная*r)

вектор Е_В = вектор Е_{пл. В} + вектор Е_{л. В}

Е_В = sqrt((Е_{пл. В})² + (Е_{л. В})²)

Правильно ли я понимаю, так как поле бесконечной равномерно заряженной плоскости однородно Е_{пл. А} = Е_{пл. В}? А Е_{л. В} = (Е_{л. А})/2, так как расстояние от линии до точки В в 2 раза больше, чем до точки А.

У меня получилось:

Е_{пл. А} = Е_{пл. В} = 56,472 * 10³

Е_{л. А} = 8,992 * 10⁶

Е_{л. В} = 4,496 * 10⁶

Е_А = 8,936 * 10⁶

Е_В = 4,496 * 10⁶

А вот с работой перемещения заряда справиться не могу, хотя гуглю вторые сутки. Решений очень похожих задач не нашёл. Вроде бы можно найти двумя способами через потенциалы в точках (но я не знаю как их найти) и через перемещение*сила*кос. угла между, но тут не знаю как решить, так как вроде бы сила в разных точках поля имеет разное направление из-за того что поле неоднородно.

Чую придётся второй раз из универа забирать документы за 1 мес. нужно сделать контрольные по 5 предметам, а у меня с физикой такая беда, как баран одну задачу 2-3 дня пытаюсь решить, а их 8, решено 4.

Мне непонятно как расположена нить? Точки А и В расположены по линии совпадающей с концом нити или нить считать бесконечно длинной (непонятно, что значит длинная нить)

длина нити имеет важное значение

Напряженность от плоскости \(E_p=\frac{\sigma}{2\pi\varepsilon{_0}\varepsilon}\) нет зависимости от расстояния

напряженность от нити (очень длинной) \(E_n=\frac{\tau}{2\pi\varepsilon{_0}\varepsilon{R}}\) \(R=a\)

Если знаки плоскости и нити одинаковые, то

\(E_A=E_p-E_n\)

\(E_B=\sqrt{E_p^2+E_n^2}\) \(R=2a\)

\(A=-\int_{r_1}^{r_2}{\frac{q\tau{dr}}{2\pi\varepsilon{_0}\varepsilon{r}}=\frac{q\tau}{2\pi\varepsilon{_0}\varepsilon}ln\frac{r_1}{r_2}\)

Работу от плоскости не рассматриваем, поскольку напряженность постоянна во всех точках.

Посмотрите на моем сайте раздел электричество http://alexandr4784.narod.ru/izerp.htm

Добавлено спустя 11 минут

Может надо учесть и плоскость

Добавлено спустя 4 минут

\(r_1=a, r_2=2a\)

Поэтому я написал, что может быть надо учесть работу и от плоскости и поместил задачу.