Преобразования Лоренца

#53289 Fedor :

Я же сказал: проходят до встречи  одинаковое расстояние относительно источника света.

А я вам показал, как это сказать грамотно.

В лабораторной системе отсчета лучи проходят разные расстояния и их задержка по времени прихода, посчитанная по формулам классической механики, ( не по СТО) равна

t₁-t₂ =4piRv/(c²-v²)

Совершенно верно. Только лучше вот в такой редакции: \(\Delta t=\frac{4\pi R^2\omega }{c^2-\omega^2R^2 }\) . И это именно по СТО. Потому что использован второй постулат СТО: скорость распространения света не зависит от скорости источника света.

Расчеты по СТО к этому никакого отношения не имеют.

Ложь.

Повторяю результаты расчета сдвига по времени (по фазе) полностью совпадают с расчетами по формулам классической механики и СТО к ним отношения не имеет.

Ложь.

Я не рассматривал движущихся стержней.

Да ну? Если в ИСО, названной нами неподвижной стержни покоятся, то в движущейся ИСО стержни двигаются.

И кто же написал вот это: «Расположенный в направлении движения системы стержень будет иметь длину L’ =L(1-v²/c²)^1/2»?

Вы не смогли опровергнуть результаты моего мысленного эксперимента.

У вас нет результата. Так что и опровергать нечего. Я вам показал, как нужно выполнять мысленные эксперименты. Учитесь, физик вы наш...

Кстати. А куда делось предыдущее ваше сообщение с подобным текстом? Вы удалили и перенесли сюда?

Я думаю Вам лучше известно кто и как вытирает мои сообщения.

Откуда же мне знать? Никаких сведений про это у меня нет.

#53293 Fedor :

#53291 zam :

Совершенно верно. Только лучше вот в такой редакции: \(\Delta t=\frac{4\pi R^2\omega }{c^2-\omega^2R^2 }\) . И это именно по СТО. Потому что использован второй постулат СТО: скорость распространения света не зависит от скорости источника света.

Это правда, однако, результаты преобразований СТО и классической механики совпадают в лабораторной системе координат.

Да какие преобразования!? Преобразования, что Лоренца, что Галилея, — это правила пересчёта физических величин при переходе от одной системы отсчёта к другой. Где тут переход? Вы же все расчёты ведёте в одной, лабораторной системе отсчёта.

Поэтому однозначного ответа о справедливости СТО нет. 

Прежде чем делать заявления по некоторому предмету, нужно этот предмет изучить, хотя бы основы.

Я написал вот это: «Расположим в неподвижной системе два светопроводящих стержняодинаковой длины L так, что они образуют прямой угол. Один из стержней направим в направлении движущейся инерциальной системы.»  Движущаяся инерциальная система у меня не содержит стержней, только наблюдателя.  Наблюдатель должен бы видеть интерференцию,  однако неподвижная система ему этого не покажет.

Полнейшая безграмотность. Любая система отсчёта содержет в себе всё, всю Вселенную, у системы отсчёта нет границ. И любой предмет находится сразу во всех системах отсчёта, которые мы захотим использовать.

Ваша неподвижная система содержит и покоящиеся стержни, и движущегнося наблюдателя. Ваша движущаяся система содержит и движущиеся стержни, и покоящегося наблюдателя.

На картинках слева  — это то, что видит наблюдатель, сидящий рядом со стержнями. Справа — это то, что видит наблюдатель, проносящийся мимо стержней. Оба видят интерференционную картинку, и она одинакова для обоих наблюдателей, что подтверждено расчётом.

Вы запутались в своих опровержениях.

Нет. Это у вас нет знаний (или умений? или желания?), чтобы понять то, что я пишу.

Попробуйте опровергнуть мой вариант эксперимента. Вот тогда и увидим. результат.

У вас нет никакого варианта, только рукомахание с аргументацией «а я так хочу». Поэтому и опровергать нечего.

#53298 Fedor :

Есть неподвижная система, в которой расположены неподвижно стержни. И Вы этого понять не можете? Зачем Вы их двигаете?

Ну и достаточно. Я психиатрии не обучался. Поэтому ничем вам помочь не могу.

Найдите себе другого собеседника.

О противоречии в преобразованиях Лоренца

Преобразования Лоренца для одномерного по пространству случая имеют вид:

x '= (x-vt)/(1-v²/c²)^1/2                                                 (1)

t'= (t-vx/c²)/(1-v²/c²)^1/2                                               (2)

Принято считать, в движущейся системе отсчета имеет место замедление времени и сокращение пространственных объектов по отношению к ходу времени и размерам тех же объектов, измеренным в неподвижной системе отсчета. Из уравнения (2), положив для движущейся системы x = vt , получим:                          t’= t(1-v²/c²)^1/2, что подтверждает сделанное утверждение. Однако с преобразованием пространственной координаты не все так просто. Известное сокращение пространственной координаты мы получим из уравнения (1) если воспользуемся сравнением длин путей, которые проходит движущаяся система, измеренными в разных системах отсчета за соответствующий системе промежуток времени :

L=x₁-x₂=vt₂-vt₁ and L’=x’₁-x’₂=vt’₂-vt’₁

Далее используя полученное преобразование для времени получаем: L ’ = L(1-v²/c²)^1/2. Пока все соответствует принятому толкованию преобразований. Пройденный движущейся системой путь, измеренный в движущейся системе оказывается короче того же пути, измеренного в неподвижной системе.

            Ничто не препятствует нам использовать прямо преобразование (1), чтобы провести аналогичное сравнение при неизменном времени, значение которого можно положить любым.

В таком случае мы получаем противоположный результат: L ’ = L(1-v²/c²)^-1/2. Размер произвольно выбранного участка в неподвижной системе оказывается меньше его же размера в движущейся системе. При таких оценках преобразования дают не сокращение, а растяжение размеров пространственных объектов в движущейся системе. Где же истина? Пространство сокращается или растягивается в движущейся системе?

#52367 Fedor :

Преобразования Лоренца и их особенности

Работа А. Эйнштейна, заложившая основу специальной теории относительности, состоит из трех самостоятельных частей: преобразований координат пространства и времени между движущимися инерциальными системами отсчета, преобразований компонентов электромагнитного поля и вывода формулы для энергии материального тела E=mc² [1].  Преобразования пространственных координат и времени впоследствии были названы преобразованиями Лоренца. Предметом настоящего сообщения является рассмотрение особенностей преобразований Лоренца и тех противоречий с реальными свойствами пространства и времени, которые возникают в результате их применения.  

Для случая, когда скорость движущейся системы направлена вдоль пространственной координаты x, координаты движущейся системы с координатами покоящейся системы преобразования Лоренца связывают следующими формулами:

x '= (x-vt)/(1-v²/c²)^1/2                                                 (1)

t'= (t-vx/c²)/(1-v²/c²)^1/2                                               (2)

Остальные две пространственные координаты преобразуются без изменения масштаба: y'=y, z'=z.Заметим, что формулы преобразований написаны для случая, когда процесс движения начинается при                                                                    t'= t= 0 и x'= x= 0. Движущаяся система имеет скорость v, поэтому, проведя в формуле (2) замену  x= vt, получим для центра координат движущейся системы:

t'= t(1-v²/c²)^1/2.                                                      (3)

Из этой формулы следует известное утверждение о том, что время в движущейся системе течет медленнее времени в неподвижной системе.

На мой взгляд, это утверждение релятивистов для СТО неверно! Вы правильно заметили, что выражение (3) справедливо только в текущий момент (начальный) времени при условии \(x=Vt\) (было принято в ТЭЛ), что и требовалось для расчета/измерения при помощи местного времени, например, для получения инвариантности скорости света в движущейся в эфире ИСО в текущий момент времени. Что недостаточно для описания физический процессов протяженных во времени, так как в момент времени отличный от нуля в точке начала координат \(x_0=0\) будет находиться не точка \(x'_0=0\)  с поправкой/погрешностью \(\pm \frac {x_0 V}{c^2}=0\), а точка  \(x'_{i,k}=\gamma(x_{i,k})=\gamma(x_0-Vt_i)=\gamma(-Vt_i)\), для которой поправка/погрешность в начальный момент (начальной синхронзации) была равна \( \frac {(-x_{i,k})V}{c^2}<0\).

Тогда уже выражение (3) будет выглядеть \(t'=\gamma(t_i- \frac {(-x_{i,k})V}{c^2})=​​​​\gamma(t_i+\frac {x_{i,k}V}{c^2})=​​​​\gamma(t_i+t_i\frac {V^2}{c^2})=\gamma t_i (1+\frac {V^2}{c^2})\). 

Вывод. Если измерять скорость света через некоторый отрезок времени от начального момента, то скорость света не будет ни константой, ни инвариантом, т. е. ПЛ не подходит для СТО. Для СТО логично было бы, чтобы поправка/погрешность, полученная для часов движущейся ИСО в начальный момент, сохранялась бы в дальнейшем при описании физических процессов. Например, \(t'=\gamma(t_i- \frac {(x_{i,k}-Vt_i)V}{c^2})\).

Ну, наверное, на первый раз будет достаточно. Когда разберемся с этим постом, можно будет переходить далее по теме.

#72043 Evalmer :

И до тех пор, пока не наступит понимание того, что речь здесь идет об одних-единственных часах, все последующие рассуждения (с самыми глубокомысленными выводами из них) не будут иметь никакого физического смысла, 

Так как Вы ведете речь об одних единственных часах, то их стрелки покажут одно время, с какой СО Вы бы не глядели. Единственные места, откуда Вы можете увидеть другие показания одних и тех же часов, это вытрезвитель и известная палата из рассказа Чехова.  

Причем здесь преобразования Доплера и зеркала? Через сколько зеркал Вы бы не смотрели на часы в неподвижной СО, стрелки часов будут показывать на те же цифры, что и в исходной СО.

#72055 Цинник :

#72051 Fedor :

Причем здесь преобразования Доплера и зеркала? Через сколько зеркал Вы бы не смотрели на часы в неподвижной СО, стрелки часов будут показывать на те же цифры, что и в исходной СО.

Ну это только а том случае если часы остановились. За то время что изображение через зеркало дойдет до наблюдателя пройдет время. И оно будет разное. По сранению с тем что дойдет напрямую до наблюдателя. Поэтому наблюдатель будет видеть одни и те же часы прказывающие разное время. А если зеркало приближается и удаляется, то еще и разный ход часов. С разной скоростью. 

О, да! Я не учел временную задержку, связанную со скоростью света и движением наблюдателя. Конечно, в момент восприятия наблюдателем показания часов их реальные стрелки убегут вперед на время полета светового сигнала. Но этот эффект происходит в рамках классической механики.

#53203 zam :

#53200 Fedor :

Согласно преобразованиям, расположенный в неподвижной системе отсчета пространственный объект, имеющий размер  L  и измеренный в движущейся со скоростью vсистеме,  имеет другой размер, который определяется выражением L’=L/G,  где

G=1/(1-v²/c²)

  Аналогичный вид имеет выражение для преобразования  времени между событиями в разных системах отсчета: DT’=DT/G. То есть, один и тот же предмет, измеренный разными системами отсчета, имеет не одинаковый результат измерения. Точно также промежуток времени между двумя событиями в неподвижной системе отсчетаDT, оказывается не равным промежутку времени между теми же событиями, измеренному в движущейся системе отсчета. Заметим, что «сокращение» размера объекта и «замедление» хода времени определяется одним и тем же множителемG^-1.

Давайте всё-таки записывать формулы аккуратно.

\(\gamma =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \\L=\frac{L_0}{\gamma } \\\Delta t= \gamma \Delta t_0\)

Здесь

\(\gamma \)  — лоренц-фактор,

\(L\)   — длина стержня в неподвижной системе отсчёта,

\(L_0\)   — длина стержня в движущейся системе отсчёта.

\(\Delta t\) - время, проходящее между двумя событиями движущегося объекта в неподвижной системе отсчёта,

\(\Delta t_0\) -  время, проходящее между двумя событиями движущегося объекта в движущейся системе отсчёта.

 

Обратите внимание, в одной формуле \(\gamma \)  в числителе, а в другой — в знаменателе.

Обратил внимание. Вот это-то и вызывает сомнение. На мой взгляд, именно в выражениях  \(L=\frac{ \Delta L_0}{ \gamma}\) (1) и \(\Delta t= \gamma \Delta t_0\) (2) у Вас допущена неясность изложения, связанная с условными обозначениями и использованием ПЛ. Например, в учебнике  (Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, Т.2), где рассматриваются две ИСО: неподвижная К и движущаяся К', сокращение продольной длины и замедление времени записывают выражениями \(\Delta x=\frac{ \Delta x'}{ \sqrt{1-v^2/c^2}}=\gamma \Delta x'\) (1) и \(\Delta t=\frac{ \Delta t'}{ \sqrt{1-v^2/c^2}}=\gamma \Delta t'\) (2), где, в отличие от вашего варианта, гамма-фактор в обоих выражениях находится в числителе.

Прошу уточнить, что Вы подразумеваете под \(L_0\) и \(\Delta t_0\) и как это соотнести с выражениями (1) и (2) из учебника. 

Причем здесь преобразования времени?  Рассматривается случай наблюдения движущимся наблюдателем за показаниями часов неподвижной системы отсчета.

#72043 Evalmer :

#72042 Alex1945 :

Вывод.  Если измерять скорость света через некоторый отрезок времени от начального момента, то скорость света не будет ни константой, ни инвариантом, т. е. ПЛ не подходит для СТО. 

Не стоит делать скоропалительных выводов, основанных на ошибочном понимании основ ПЛ (преобразований Лоренца). Пока до автора темы (дядя Fedor) не дойдет, что часы, находящиеся в точке х1 (пространственная координата: \(x_1\)), показывают в этой точке время (имеют временну́ю координату: \(t_1\)), то в движущейся инерциальной системе отсчета (ИСО) они (эти самы часы) будут находится в точке:

\(\displaystyle x'_1={x_1-t_1\cdot v\over\sqrt{1-v^2/c^2}}\not= x_1\)

где и будут показывать время:

\(\displaystyle t'_1={t_1-x_1\cdot v/c^2\over\sqrt{1-v^2/c^2}}\not= t_1 \)

И до тех пор, пока не наступит понимание того, что речь здесь идет об одних-единственных часах, все последующие рассуждения (с самыми глубокомысленными выводами из них) не будут иметь никакого физического смысла, 

В том то и дело, что речь идет о часах двух ИСО, находящихся в момент \(t_i\) в одной точке, общей для обеих ИСО.

Так, например, в начальный момент и в момент световой синхронизации, когда начала координат этих ИСО с часами в находящимися в началах координат будут связаны уравнениями ПЛ: 

\(\displaystyle x'_0={(x_0=0)-(t_0=0)\cdot v\over\sqrt{1-v^2/c^2}}= x_0=0\)

где часы начала координат и будут показывать время: 

\(\displaystyle t'_0={(t_0=0)-(x_0=0)\cdot v/c^2\over\sqrt{1-v^2/c^2}}= t_0=0 \) .

И что Вам здесь не понравилось? Смысл моего вывода в том, что преобразование времени в ПЛ справедливо только для момента синхронизации в начальный момент времени \(\displaystyle t'_0= t_0=0 \), в следующий момент времени в точке будет находиться уже другая точка x'_k , т. е. в часы в этой точке необходимо будет заменить поправку синхронизации на новую, т. е. в каждый новый момент времени надо будет проводить пересинхронизацию всех часов движущейся ИСО.

В момент \(t_0=0 \) точка  \(x'_0=x_0=0 \), а поправка синхронизации будет равна \((-\frac{0\cdot v/c^2}{\sqrt{1-v^2/c^2}}= 0) \), т. е. \(\displaystyle t'_0={t_0-x_0\cdot v/c^2\over\sqrt{1-v^2/c^2}}=0\).

В момент \(t_i>0 \) точка  \(x'_i=\frac{(x_0=0)-(t_i>0)\cdot v}{\sqrt{1-v^2/c^2}}=-\frac{t_i\cdot v}{\sqrt{1-v^2/c^2}}<0\), а поправка синхронизации для часов в точке \((-x'_i)\) бывшая положительной, согласно ПЛ при \(x_0=0 \), должна при помощи пересинхронизации измениться из положительной \((-\frac{(-x_{0,k})\cdot v/c^2}{\sqrt{1-v^2/c^2}}> 0 )\) на нулевую \((-\frac{(x_0=0)\cdot v/c^2}{\sqrt{1-v^2/c^2}}= 0) \), а время в точке \((-x'_i)\)  должно будет стать  \(\displaystyle t'_i=\frac{(t_i>0)-(x_0=0)\cdot v/c^2}{\sqrt{1-v^2/c^2}}=\frac{t_i}{\sqrt{1-v^2/c^2}}\), т. е. движущиеся часы будут идти быстрей неподвижных, что вряд ли можно отнести к достоинствам ПЛ. 

Спросите причем здесь пересинхронизация, часов в точке \((-x'_i)\) в момент \(t_i>0 \)? А каким образом поправка световой синхронизации с положительной \((-\frac{(-x_{0,k})\cdot v/c^2}{\sqrt{1-v^2/c^2}}> 0 )\) может измениться на нулевую \((-\frac{0\cdot v/c^2}{\sqrt{1-v^2/c^2}}= 0) \)?

#72090 Alex1945 :

#72082 Fedor :

 

 

Величина t’=–x_jkV/c² относится только к моменту. Поэтому последующие ваши оценки ошибочны. Вообще не только в точке x’=0, но и в любой фиксированной точке x’  СО K’ выполняется зависимость t'= t(1-v²/c²)^1/2.

Не понял, гда у меня говорится о t’=–x_jkV/c² ? Но Вы правы, когда говорите, что для любой точки в ИСО К' зависимость t'= t(1-v²/c²)^1/2   выполняется  только в момент t=0, для которого была проведена световая синхронизация. Однако в любой другой момент \(t_i>0\) синхронность движущихся часов, полученная в начальный момент, нарушается и для выполнения ПО необходимо будет проводить пересинхронизацию всех часов ИСО К', т. е. без которой никак не получить отрезхки местного времени ИСО К' меньше отрезаков собственного времени ИСО К в \(\gamma\)  раз.

Я потом уточнил поправкой:" но и в любой фиксированной точке x’  СО K’ выполняется зависимость для интервала времени между двумя событиями  dt'= dt(1-v²/c²)^1/2." Вы же ошибочно получили t'= t(1+v²/c²)/(1-v²/c²)^1/2. Ошибка от неправильного знака в –x_jkV/c²

#72098 Fedor :

#72090 Alex1945 :

#72082 Fedor :

 

 

Величина t’=–x_jkV/c² относится только к моменту. Поэтому последующие ваши оценки ошибочны. Вообще не только в точке x’=0, но и в любой фиксированной точке x’  СО K’ выполняется зависимость t'= t(1-v²/c²)^1/2.

Не понял, гда у меня говорится о t’=–x_jkV/c² ? Но Вы правы, когда говорите, что для любой точки в ИСО К' зависимость t'= t(1-v²/c²)^1/2   выполняется  только в момент t=0, для которого была проведена световая синхронизация. Однако в любой другой момент \(t_i>0\) синхронность движущихся часов, полученная в начальный момент, нарушается и для выполнения ПО необходимо будет проводить пересинхронизацию всех часов ИСО К', т. е. без которой никак не получить отрезхки местного времени ИСО К' меньше отрезаков собственного времени ИСО К в \(\gamma\)  раз.

Я потом уточнил поправкой:" но и в любой фиксированной точке x’  СО K’ выполняется зависимость для интервала времени между двумя событиями  dt'= dt(1-v²/c²)^1/2." Вы же ошибочно получили t'= t(1+v²/c²)/(1-v²/c²)^1/2. Ошибка от неправильного знака в –x_jkV/c²

Вы просто не учитываете положение движущихся часов от начала координат ИСО К'.

Часы ИСО К' после световой синхронизации, расположенные слева от начала координат, часы начала координат, согласно ПЛ \(t'=\gamma(t+\frac{xV}{c^2})\),  опережают на величину погрешности синхронизации, а часы, расположенные справа от начала координат \(t'=\gamma(t-\frac{xV}{c^2})\), отстают.

#72130 Fedor :

#72113 Alex1945 :

 

Преобразование времени \(t'=\gamma(t-\frac{xv}{c^2})\) в ПЛ служит для расчета мгновенных значений местного (координатного) времени \(t'\) для часов в движущейся ИСО К', которые в момент \(t\) находятся в точке \(x \). Насколько я понимаю физический смысл преобразования времени в ПЛ  \(t'=\gamma(t-\frac{xv}{c^2})\),  для конкретной точки \(x \)  Ваше выражение dt'= dt(1-v²/c²)^1/2 должно выглядеть   \(dt'=\gamma dt=\frac{dt}{\sqrt{1-v^2/c^2}}\), т. е. движущиеся часы должны идти быстрей и только поправка \(\pm\gamma \frac{xv}{c^2}\) позволяет обеспечить требуемое уменьшение отрезка местного времени движущейся ИСО в сравнении с отрезком собственного времени неподвижной ИСО.

Вы забываете, что начало координат движущейсяСО x’=0 движется по х такx=vt. Теперь это х = vt подставьте в формулу

t’=( t- vx/ c²)/(1-v²/c²)^0.5= =(t-vvt/c²)/(1-v²/c²)^0.5=t(1-v²/c²)/(1-v²/c²)^0.5= t(1-v²/c²)^0.5

Как видите движущиеся часы идут медленнее.

 

Вы правы, что в каждый следующий момент времени \(t_i\) координата текущей точки ИСО К' в ИСО К будет равна \(x=x_{i,k}=x_{0,k}+vt_i\), а в ИСО К' будет равна  \(x'_{i,k}=\gamma(x-vt_i)=\gamma(x_{i,k}-vt_i)\). Рассмотрим эти же ИСО в момент времени \(t_2=l/v=0,77\cdot 10^{-8}\) сек.

В любой момент

x ′ _i,k=γ(x−vti), x=x₀+vt_i, x′_i,k=γ(x−vti) =γ(x₀+vt_i-vt_i)=γ(x₀).

Снова Вы ошибаетесь. Подставляйте в формулы правильные значения. Кстати в СТО никто ничего не синхронизирует. Формулы преобразования получаются без световой синхронизации. Достаточно одного положения c=const.

Итак, преобразования времени в ПЛ предназначены для расчета мгновенных значений времени  t′=f(t), которые будут показывать часы в точке x′_k ИСО К', которая в заданный момент времени t_i  находится в текущей точке x. 

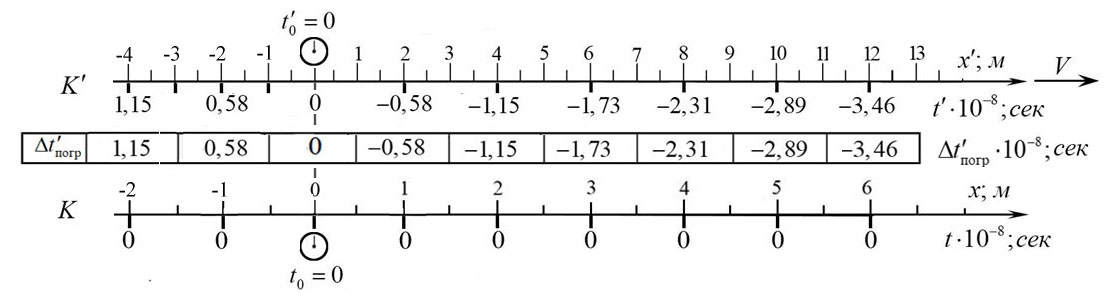
Рисунок 1. Начальный момент   x’=x=0, t’=t=0.

Вы согласны, что для этих двух ИСО при скорости \(v=2,6\cdot 10^{-8}\) и \(\gamma=2\) после синхронизации часов собственных часов этих ИСО и синхронизации начал координат этих ИСО  в начальный момент, значения показаний часов ИСО К', рассчитанные мной по формуле \(t'=\gamma(t-\frac{xv}{c^2})\), были мной рассчитаны правильно? Если не согласны, то укажите, где я ошибся. Ниже мной приведен расчет местного времени для точки \(x_{-4}\), т. е. \(t'_{0,-4}=\gamma(t_0-\frac{-2v}{c^2})=\gamma(t_0+\frac{2v}{c^2})=1,15\cdot 10^{-8}\) сек.

Если у меня есть ошибки, то их начало заложено в этой расчетной схеме и моем понимании физического смысла ПЛ. Давайте с этого и начнем.

#72140 Fedor :

#72134 Alex1945 :

 

Если у меня есть ошибки, то их начало заложено в этой расчетной схеме и моем понимании физического смысла ПЛ. Давайте с этого и начнем.

Ваша таблица построена правильно. Только нужно помнить, что преобразования преобразуют значения времени, а не показания часов. Ход часов и их показания Вы можете устроить как Вам угодно, в том числе и в соответствии с временем в системе K'.

При этом надо помнить, что преобразованиях времени в ПЛ рассчитываются мгновенные значения времени (именно показания часов) в движущейся ИСО К'  \(t'_i\)  на часах ИСО К', размещенных в момент  \(t_i\) в точке \(x_k\) (см. рисунок 1).  Для этого в этих двух ИСО собственные часы предварительно  должны быть синхронизированы световым сигналом в начальный момент времени (\(t_0=t'_0=0;\) \(x_0=x'_0=0\)), а сами ИСО синхронизированы между собой согласно рисунку 1. 

Рисунок 1. Положение движущихся и неподвижных часов относительно друг друга и мгновенные показания часов в начальный момент (\(t_0=t'_0=0;\) \(x_0=x'_0=0\)). 

 Я обращаю ваше внимание на то, что в системе K'  длительность секунд и длина метров отличается от соответствующих единиц измерения в системе К. Это видно прямо из таблицы. Один метр в системе К равен двум метрам  СО K’. То же самое выполняется и с длительностями секунд. Таким образом, система K' не эквивалентна системе К.

Согласен, ИСО К и ИСО К' не эквивалентны и поэтому не равноправны, т. е. первый постулат в ПЛ не обеспечивается, так как метр длины и секунда времени в этих ИСО отличаются физически!  Поэтому ни о каком ПО и речи не может быть! 

Но, если Вы сделаете обратное преобразование из K’  в систему К путем замены знака скорости на противоположный, то Вы вернетесь в СО К. Если же Вы предположите K’ неподвижной СО (то есть, полностью эквивалентной К),  то получите сокращенные координаты новой СО, подобно преобразованию из К в K'.

Если изображенные на рисунке 1 ИСО К и К' соответствуют реальным сокращению длины и изменению течения времени, то после переименования ИСО К в движущуюся, а ИСО К' в неподвижную реально ни длина, ни течение времени не изменятся, просто преобразования ПЛ покажут кажущиеся (иллюзорные, в реальности не существующие) сокращение длины и кажущееся изменение течения времени, как это и было принято в ТЭЛ.

Вывод. Преобразования создают новую систему отсчета с другими размерами единиц измерения и с разными  стартовыми показаниями времени, зависящими от пространственной координаты.

Я бы сказал иначе: ПЛ — это попытка создать такую ИСО, которая в первую очередь обеспечила бы объяснение результатов М-М при наличии эфира (т. е. невозможность обнаружения абсолютной скорости физическими опытами, находясь внутри ИСО) и условную симметрию реальных и кажущихся РЭ.