Относительное замедление времени

#66331 AlexOsipovich :1) «Сто раз уже объяснено. Условия, в которых находились часы, не одинаковы. Первые часы не испытывали ускорений, вторые — испытывали.»
Во-первых в моей задаче одинаковы — в ней нет ускорений и торможений.
Речь не про вашу задачу, а вот про это: «Представьте себе ракету в которую закидывают часы без наблюдателя, а вторые остаются на земле. Ракета полетала и прилетела назад, а при сравнении одни часы отстают».
Во-вторых — ускорение никак не влияет на ход часов:
«Однако, как показывают экспериментальные данные, ускорение как таковое не влияет на скорость хода часов [28] . Таким образом, в данном случае ускорение является всего лишь индикатором некоторого явления, которое вносит асимметрию в состояния путешественника и домоседа.»
Это цитата из Вики ошибочна.
Сколько раз вам повторять — читайте учебники. Угаров ( https://scask.ru/l_book_spec.php?id=22 ). Цитата оттуда (стр. 83): «Ускорение, безусловно, влияет на ход часов». другие двигаются относительно вагона.
А в моей задаче Вы утверждаете — что и результаты измерения темпа хода часов одинаковые. В поездах разные, а в моей задаче про пункты АБ и корабль резко стали одинаковые. Почему можете объяснить? Какие-то двойные стандарты.
Читайте решение https://sfiz.ru/forums/post/66157#66157. Там всё написано. Если есть вопросы по решению, задавайте.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Я придумал задачу специально под Вас, поможите решить?
Корабль длиной 1 ае (измеренной в покое) движется равномерно и прямолинейно относительно неподвижной ИСО_АБ со скоростью 200 000 км/с. Расстояние между АБ также 1 ае.
В носу и в хвосте корабля находятся часы. Также часы находятся на пунктах АБ.
1) Когда голова корабля достигает пункта А, наблюдатель запускает часы головы и одновременно запускаются часы пункта А.
2) Когда голова корабля достигает пункта Б, наблюдатель выключает часы головы и одновременно запускаются часы пункта Б.
3) Когда хвост корабля достигает пункта А, наблюдатель включает часы хвоста и одновременно выключаются часы пункта А.
4) Когда хвост корабля достигает пункта Б, наблюдатель выключает часы хвоста и одновременно выключаются часы пункта Б.
В итоге имеем:
1) Какое время показывают часы Г?
2) Какое время показывают часы Х?
3) Какое время показывают часы А?
4) Какое время показывают часы Б?

#66339 AlexOsipovich :Я придумал задачу специально под Вас, поможите решить?
С удовольствием. Только сначала оформлю задачу как положено.
Корабль длиной 1 ае (измеренной в покое) движется равномерно и прямолинейно относительно неподвижной ИСО_АБ со скоростью 200 000 км/с. Расстояние между АБ также 1 ае.
Корабль длиной \(L_{к0}\) (собственная длина, результат измерения собственными линейками корабля) движется с равномерно прямолинейно относительно ИСО материальных точек А и Б со скоростью \(v\).
Расстояние между точками А и Б (собственное расстояние, результат измерения собственными линейками системы АБ) равно \(L_{АБ0}=L_{к0}\) .
В носу и в хвосте корабля находятся часы.
Военного моряка на вас нет… На носу и на корме корабля находятся синхронизированные в системе отсчёта корабля часы \(Н\) и \(К\) .
Также часы находятся на пунктах АБ.
В пунктах А и Б находятся синхронизированные в системе отсчёта АБ часы \(А\) и \(Б\) .
1) Когда голова корабля достигает пункта А, наблюдатель запускает часы головы и одновременно запускаются часы пункта А.
2) Когда голова корабля достигает пункта Б, наблюдатель выключает часы головы и одновременно запускаются часы пункта Б.
3) Когда хвост корабля достигает пункта А, наблюдатель включает часы хвоста и одновременно выключаются часы пункта А.
4) Когда хвост корабля достигает пункта Б, наблюдатель выключает часы хвоста и одновременно выключаются часы пункта Б.
Не надо ничего включать и выключать. Это вас путает. Достаточно просто записывать на листочек показания часов.
Задача сто-007
Корабль длиной \(L_{к0}\) (собственная длина, результат измерения собственными линейками корабля) движется с равномерно прямолинейно относительно ИСО материальных точек А и Б со скоростью \(v\).
На носу и на корме корабля находятся синхронизированные в системе отсчёта корабля часы \(Н\) и \(К\) .
Расстояние между точками А и Б (собственное расстояние, результат измерения собственными линейками системы АБ) равно \(L_{АБ0}=L_{к0}\) .
В пунктах А и Б находятся синхронизированные в системе отсчёта АБ часы \(А\) и \(Б\) .
Имеется четыре события:
«НА» - встреча носа корабля и пункта А;
«НБ» - встреча носа корабля и пункта Б;
«КА» - встреча кормы корабля и пункта А;
«КБ» - встреча кормы корабля и пункта Б;
Требуется определить промежутки времени \(\Delta t'_{НА-НБ}, \;\Delta t'_{КА-КБ}, \;\Delta t_{НА-КА}, \;\Delta t_{НБ-КБ}\) .
(штрихованные величины относятся к ИСО корабля, без штрихов — к ИСО АБ).
Вот теперь моежете решать. А я буду проверять.
А числа можно подствить потом, когда будут получены формулы-решения (самое тупое занятие).

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
По СТО она обсчитывается очень просто:
1) Какое время показывают часы Г? 559 сек
2) Какое время показывают часы Х? 559 сек
3) Какое время показывают часы А? 750 сек
4) Какое время показывают часы Б? 750 сек
Так?

#66363 AlexOsipovich :По СТО она обсчитывается очень просто:
Совершенно верно. Задача элементарная. Да вот беда — вы СТО не знаете.
1) Какое время показывают часы Г? 559 сек
2) Какое время показывают часы Х? 559 сек
3) Какое время показывают часы А? 750 сек
4) Какое время показывают часы Б? 750 секТак?
Нет.
Кроме того, необходимо привести не ответы, а решение.
А ответ должен быть формулой, а не числом.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
По моему решению, так приведите пожалуйста свое

#66365 AlexOsipovich :По моему решению, так приведите пожалуйста свое
Вы же просили помочь решить, а не решить за вас.
Так где же ваши попытки решения? Как я смогу узнать, в каком месте вы ошибаетесь?

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Могу еще графическое решение показать:
АГ — встреча пункта А и головы корабля
БГ — встреча пункта Б и головы корабля
Голубая линия — это МЛ движущегося корабля
По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Если меняем системы ролями:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Интервал между событиями инвариант 750 сек.
Так какое все-таки время покажут часы головы корабля? 750 сек или 559 сек?

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Я веду расчет по формуле релятивистского замедления времени, она идеально подходит для данной ситуации

#66367 AlexOsipovich :Могу еще графическое решение показать:
АГ — встреча пункта А и головы корабля
БГ — встреча пункта Б и головы корабля
Голубая линия — это МЛ движущегося корабля
Голубая линия — это не мировая линия корабля, это мировая линия головы (носа) корабля. Неплохо нарисовать ещё и мировую линию кормы корабля.
По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Если меняем системы ролями:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Интервал между событиями инвариант 750 сек.
Не надо гадать. Надо решить задачу.
Так какое все-таки время покажут часы головы корабля? 750 сек или 559 сек?
Вот решите задачу и узнаете.

#66368 AlexOsipovich :Я веду расчет по формуле релятивистского замедления времени, она идеально подходит для данной ситуации
Так напишите эту формулу.
Расскажите, что обозначают входящие в эту формулу буквы.
Напишите, при каких условиях эта формула применима, а при каких нет.
Расскажите, почему она применима для вашей задачи.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Смотрите, расчет такой:
Т.к ИСО_корабля движется относительно ИСО_АБ равномерно и прямолинейно, значит я вправе применить формулу релятивистского замедления времени для движения с постоянной скоростью.
Применяю:
\(t' = {t \sqrt{1-{v^2 \over c^2}} } = 750 \sqrt{1-{0.6666^2 \over 1^2}} = 750 * 0.7453 = 559 сек.\)
t - время, проходящее между двумя событиями движущегося объекта в неподвижной системе отсчёта
t' - время, проходящее между двумя событиями движущегося объекта с точки зрения наблюдателя, связанного с движущимся объектом/
Если системы поменять ролями, принять на неподвижную СО_корабля, ситуация зеркальная
По итогу имеем результат:
По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Если меняем системы ролями:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Согласны с ним?

#66371 AlexOsipovich :Т.к ИСО_корабля движется относительно ИСО_АБ равномерно и прямолинейно, значит я вправе применить формулу релятивистского замедления времени для движения с постоянной скоростью.
Разве этого достаточно для того, чтобы применить фйормулу?:
Я уже задавал вам вопрос — дла какой пары событий применима данная формула? Вы вопрос проигнорировали (вроде бы написали «для всех»).
Применяю:
\(t' = {t \sqrt{1-{v^2 \over c^2}} } = 750 \sqrt{1-{0.6666^2 \over 1^2}} = 750 * 0.7453 = 559 сек.\)
t - время, проходящее между двумя событиями движущегося объекта в неподвижной системе отсчёта
t' - время, проходящее между двумя событиями движущегося объекта с точки зрения наблюдателя, связанного с движущимся объектом/
Итак, вы взяли формулу и комментарии к ней из Вики — вот фотография оттуда:

Причём формулу переписали по-своему.
Теперь читайте внимательно, что обозначают буковки в этой формуле.
\(\Delta t=\frac{\Delta t_0}{\sqrt{1-\frac{v^2}{c^2}}}\)
\(\Delta t_0\) — результат измерения промежутка времени между парой событий в той ИСО, в которой эта пара событий происходит в одном и том же месте.
\(\Delta t\) — результат измерения промежутка времени между парой событий в той ИСО, которая движется относительно первой со скоростью \(v\).
Вот интересно. Вы сами приводили ссылку на методичку ЦЕРНа:

Там же приведён вывод обсуждаемой формулы. Что же вы сами не читаете материалы, на которые ссылаетесь?
Теперь посмотрим, применимали эта формула к нашему случаю.
Рассматривается пара событий — «АГ» и «БГ».
Эти два события в ИСО корабля происходят в одном и том же месте, то есть, формула применима и \(\Delta t'_{АГ-БГ}=\Delta t_0\) . (штрихованные обозначения относятся к ИСО корабля).
Соответственно, \(\Delta t_{АГ-БГ}=\Delta t\) .
Промежуток времени в ИСО_АБ находится элементарно: \(\Delta t_{АГ-БГ}=\frac{L_{АБ0}}{v} \) (просто по определению термина «скорость»).
Подставляя в обсуждаемую скорость, получаем:
\(\Delta t_{АГ-БГ}=\frac{\Delta t'_{АГ-БГ}}{\sqrt{1-\frac{v^2}{c^2}}}\).
Отсюда \(\Delta t'_{АГ-БГ}=\Delta t_{АГ-БГ}\sqrt{1-\frac{v^2}{c^2}}=\frac{L_{АБ0}}{v} \sqrt{1-\frac{v^2}{c^2}}\) .
Если системы поменять ролями, принять на неподвижную СО_корабля, ситуация зеркальная
Как не меняйте, результат расчёта не изменится. Обзатите внимание: в ИСО_АБ события АГ и БГ происходят в разных местах.
А теперь разберите оставшиеся три пары событий и посмотрите, что получается с ними.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Так я написал тоже самое, сколько по Вашим подсчетам получится?
По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Так?

#66367 AlexOsipovich :
Вот диаграмма Минковского для вашей задачи:
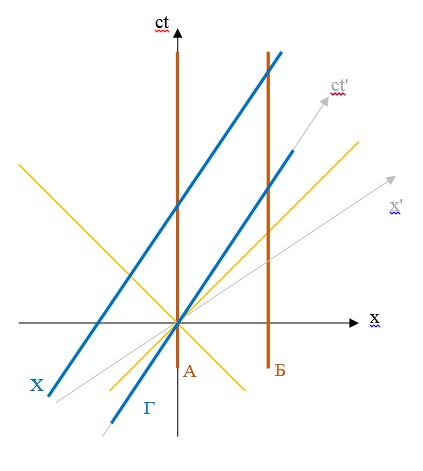
Жёлтые линии — это световой конус.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Диаграмма красивая спасибо! Так какие значения мы по ней получим, не томите:
По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Если меняем системы ролями:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Интервал между событиями инвариант 750 сек.
Все так?

#66382 AlexOsipovich :Так я написал тоже самое, сколько по Вашим подсчетам получится?
По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Так?
Так. А вы числа сами подставить не можете?

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Мой расчет был точно таким же как у Вас, я изначально все подставил. Просто у Вас уточняю
Осталось разобрать последнюю часть.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Если меняем системы ролями, теперь двигаются пункты АБ, а корабль неподвижен:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Верно?

#66385 AlexOsipovich :По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Да.
Между событиями АГ и БГ проходит:
по измерениям из точек А и Б 750 секунд;
по измерениям из корабля 559 секунд.
Если меняем системы ролями:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Получаем те же самые результаты:
Между событиями АГ и БГ проходит:
по измерениям из точек А и Б 750 секунд;
по измерениям из корабля 559 секунд.
Интервал между событиями инвариант 750 сек.
Инвариант.
Интервал: \(\Delta s= \sqrt{c^2\Delta t^2-\Delta x^2}=Const\)
Чем больше расстояние между событиями, тем больше промежуток времени между событиями.
В ИСО_АБ: \(\Delta t=750\; c,\Delta x=150\; 000\; 000\; 000\; м \) .
В ИСО корабля \(\Delta t'=559\; c,\Delta x'=0\; м\) .
Интервал: \(\Delta s_{АГ-БГ}=\sqrt{(300 000 000\; м/с)^2(750\; c)^2-(150\; 000\; 000\; 000\; м)^2))}=\sqrt{(300 000 000\; м/с)^2(559\; c)^2-(0\; м)^2))}=167\; 700\; 000\; 000\; м\) .

#66390 AlexOsipovich :Если меняем системы ролями, теперь двигаются пункты АБ, а корабль неподвижен:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Верно?
Нет. Нужно решать задачу, а не угадывать ответ.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
#66394 zam :#66385 AlexOsipovich :По показаниям наблюдателей неподвижной: ИСО_АБ - между событиями АГ и БГ проходит 750 сек, в движущейся ИСО корабля 559 сек.
Да.
Между событиями АГ и БГ проходит:
по измерениям из точек А и Б 750 секунд;
по измерениям из корабля 559 секунд.
Если меняем системы ролями:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.Получаем те же самые результаты:
Между событиями АГ и БГ проходит:
по измерениям из точек А и Б 750 секунд;
по измерениям из корабля 559 секунд.
Интервал между событиями инвариант 750 сек.
Инвариант.
Интервал: \(\Delta s= \sqrt{c^2\Delta t^2-\Delta x^2}=Const\)
Чем больше расстояние между событиями, тем больше промежуток времени между событиями.
В ИСО_АБ: \(\Delta t=750\; c,\Delta x=150\; 000\; 000\; 000\; м \) .
В ИСО корабля \(\Delta t'=559\; c,\Delta x'=0\; м\) .
Интервал: \(\Delta s_{АГ-БГ}=\sqrt{(300 000 000\; м/с)^2(750\; c)^2-(150\; 000\; 000\; 000\; м)^2))}=\sqrt{(300 000 000\; м/с)^2(559\; c)^2-(0\; м)^2))}=167\; 700\; 000\; 000\; м\) .
Вы неправильно интерпретируете свою же диаграмму. То что у вас на ней нарисовано — это показания и проекции из одной неподвижной ИСО_АБ для движущейся ИСО_корабля
А есть ровно такая же диаграмма, только для неподвижной ИСО_корабля и движущейся ИСО_АБ.
Поэтому когда мы поменяли системы ролями — Вы ошиблись.
отредактировал(а) AlexOsipovich: 2024-08-23 15:11 GMT

#66396 AlexOsipovich :#66394 zam :Интервал: \(\Delta s_{АГ-БГ}=\sqrt{(300 000 000\; м/с)^2(750\; c)^2-(150\; 000\; 000\; 000\; м)^2))}=\sqrt{(300 000 000\; м/с)^2(559\; c)^2-(0\; м)^2))}=167\; 700\; 000\; 000\; м\) .
Вы неправильно интерпретируете свою же диаграмму.
Я интерпретирую интерпретацию? Доаольно странно звучит, потому что диаграммы Минковского — это уже интерпретация (перевод языка уравнений на язык рисунков).
То что у вас на ней нарисовано — это показания и проекции из одной неподвижной ИСО_АБ для движущейся ИСО_корабля
То, что у меня нарисовано — это результаты расчётов по формулам (уравнениям СТО). Причём сразу в двух ИСО. Может, вы не заметили, но там светло-серым изображены и оси координат ИСО корабля (штрихованные).
А есть ровно такая же диаграмма, только для неподвижной ИСО_корабля и движущейся ИСО_АБ.
Конечно, и она уже изображена.
Поэтому когда мы поменяли системы ролями — Вы ошиблись.
Где я ошибся? Почему вы это сказали уже сто раз и ни разу не подтвердили аргументами (уравнениями, расчётами, ссылками на учебники)?

 14 сообщений
14 сообщенийОткуда: Псковская губерния деревня Хрюково
Кто: мытарство
Возраст: 45
Описание условия хватило только на это

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
#66399 zam :#66396 AlexOsipovich :#66394 zam :Интервал: \(\Delta s_{АГ-БГ}=\sqrt{(300 000 000\; м/с)^2(750\; c)^2-(150\; 000\; 000\; 000\; м)^2))}=\sqrt{(300 000 000\; м/с)^2(559\; c)^2-(0\; м)^2))}=167\; 700\; 000\; 000\; м\) .
Вы неправильно интерпретируете свою же диаграмму.
Я интерпретирую интерпретацию? Доаольно странно звучит, потому что диаграммы Минковского — это уже интерпретация (перевод языка уравнений на язык рисунков).
То что у вас на ней нарисовано — это показания и проекции из одной неподвижной ИСО_АБ для движущейся ИСО_корабля
То, что у меня нарисовано — это результаты расчётов по формулам (уравнениям СТО). Причём сразу в двух ИСО. Может, вы не заметили, но там светло-серым изображены и оси координат ИСО корабля (штрихованные).
А есть ровно такая же диаграмма, только для неподвижной ИСО_корабля и движущейся ИСО_АБ.
Конечно, и она уже изображена.
Поэтому когда мы поменяли системы ролями — Вы ошиблись.
Где я ошибся? Почему вы это сказали уже сто раз и ни разу не подтвердили аргументами (уравнениями, расчётами, ссылками на учебники)?
Вот если Вы свои серые оси ct', x' повернете в положение в котором сейчас ct, x что будет с осями ct, x?
Пришлете обновленную диаграмму? Посмотрим, что скажут наблюдатели из ИСО_корабля?

#66402 AlexOsipovich :Вот если Вы свои серые оси ct', x' повернете в положение в котором сейчас ct, x что будет с осями ct, x?
Пришлете обновленную диаграмму? Посмотрим, что скажут наблюдатели из ИСО_корабля?
Ровно то же самое.
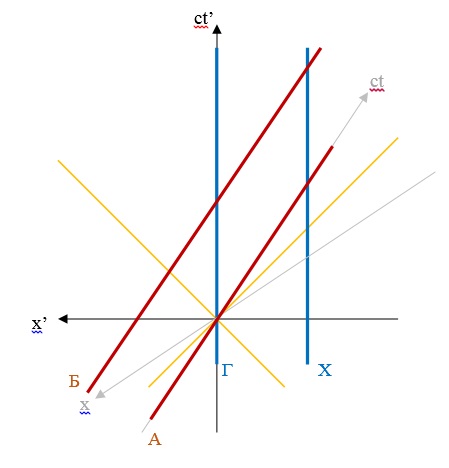
Задача ведь совершенно симметрична.


 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
#66403 zam :#66402 AlexOsipovich :Вот если Вы свои серые оси ct', x' повернете в положение в котором сейчас ct, x что будет с осями ct, x?
Пришлете обновленную диаграмму? Посмотрим, что скажут наблюдатели из ИСО_корабля?
Ровно то же самое.

Задача ведь совершенно симметрична.

И так,
Если меняем системы ролями, теперь двигаются пункты АБ, а корабль неподвижен:
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Верно?

#66404 AlexOsipovich :#66403 zam :Задача ведь совершенно симметрична.
И так,
«Итак» пишется слитно, без пробела.
Если меняем системы ролями, теперь двигаются пункты АБ, а корабль неподвижен:
Да.
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Вам нужно не угадать ответ, а решить задачу.
При решении учтите:
1) в ИСО корабля расстояние между пунктами А и Б не \(L_0\), а меньше;
2) в ИСО корабля часы в пунктах А и Б не синхронизированы.
Методическая рекомендация: не пользуйтесь следствиями из преобразований Лоренца (они применимы в исключительных случаях, которых вы не знаете и узнать не хотите). Пользуйтесь непосредственно преобразованиям Лоренца, они работают везде и всегда.
Верно?
Нет.

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
#66407 zam :#66404 AlexOsipovich :#66403 zam :Задача ведь совершенно симметрична.
И так,
«Итак» пишется слитно, без пробела.
Если меняем системы ролями, теперь двигаются пункты АБ, а корабль неподвижен:
Да.
По показаниям наблюдателей неподвижной: ИСО_корабля — между событиями АГ и БГ — проходит 750 сек, в движущейся ИСО_АБ 559 сек.
Вам нужно не угадать ответ, а решить задачу.
При решении учтите:
1) в ИСО корабля расстояние между пунктами А и Б не \(L_0\), а меньше;
2) в ИСО корабля часы в пунктах А и Б не синхронизированы.
Методическая рекомендация: не пользуйтесь следствиями из преобразований Лоренца (они применимы в исключительных случаях, которых вы не знаете и узнать не хотите). Пользуйтесь непосредственно преобразованиям Лоренца, они работают везде и всегда.
Верно?
Нет.
1) в ИСО корабля расстояние между пунктами А и Б не \(L_0\), а меньше; —
А в предыдущем расчете Вы уменьшение расстояния между Г и Х учитывали — нет! Лукавите
2) в ИСО корабля часы в пунктах А и Б не синхронизированы. - Синхронизации в задаче вообще нет
3) Ответ я не угадал, а рассчитал
отредактировал(а) AlexOsipovich: 2024-08-23 19:31 GMT

#66408 AlexOsipovich :1) в ИСО корабля расстояние между пунктами А и Б не \(L_0\), а меньше; —
А в предыдущем расчете Вы уменьшение расстояния между Г и Х учитывали — нет! Лукавите
А где там потребовалось это учитывать? Там про точку Х вообще речи не шло. Вычислялся промежуток времен между событиями АГ и БГ. Где тут буква «Х»?
2) в ИСО корабля часы в пунктах А и Б не синхронизированы. - Синхронизации в задаче вообще нет
Тогда вы не сможете выполнить никаких измерений промежутков времени между разноместными событиями. В ИСО корабля события АГ и БГ произошли в одном месте. В ИСО_АБ события АГ и БГ произошли в разных местах.
3) Ответ я не угадал, а рассчитал
Так покажите расчёт. То есть, формулы, с описанием того, что там обозначают буквы. Числа совсем не обязательно — они только мешают.





