О чем говорят эксперименты Саньяка

Ау, модераторы! Посмотрите, что делается здесь и здесь: Законы Ньютона в расширяющейся Вселенной

#63468 Fedor :#63441 zam :
В вашей задаче две инерциальные системмы отсчёта. Показания секундомеров в них одинаковы, потому что это инварианты.
Моменты старта фотонов также совпадают в обеих системах отсчета.
Нет. Они совпадают в системе отсчёта стержня (по условию задачи). В лабораторной системе отсчёта они совпадать не могут.
Очень аргументированно и доказательно. Только для таких дураков как я непонятно, почему в момент старта фотонов t’=t=0 и это оказывается не одновременно.
В системе отсчёта стержня момент старта фотонов t0' и моменты пуска секундомеров tP1' и tP2' совпадают (равны нулю).
В лабораторной системе отсчёта момент старта фотонов t0 = 0 несовпадает с моментами пуска секундомеров tP1 = -vL/c2 и tP2 = vL/c2.
Сравнивать моменты времени в разных системах отсчёта (t и t') бессмысленно. Хотя бы по той причине, что момент начала счёта времени (ноль на оси времени) мы выбираем произвольно (как нам удобно, так и выберем).
Моменты включения секундомеров разные, но беда состоит в том, что по концам стержней находится по одному секундомеру. Кроме того, показания стрелок секундомеров в момент включения направлены на цифру нуль. Как тут быть? Объясните, пожалуйста, как теперь посчитать показания стрелок в момент прихода сигналов к секундомерам?
Это написано в решении задачи — сообщение #63295 https://sfiz.ru/forums/post/63295#63295 .
Давайте посмотрим на формулу преобразования ts1.
ts1= Г(t’s1-vxs1/c2).
Аналогичный вид имеет выражение для ts2, где вместо минуса стоит плюс. Что показывают эти выражения? Эти выражения показывают длительность промежутка времени между моментами t’s1= t’s2=0 и моментом прихода сигналов к секундомерам.
Всё так. (Только апостроф пропустили: ts1= Г(t’s1-vx's1/c2).

 315 сообщений
315 сообщенийОткуда: аг. Засковичи, ул Зеленая, д 6
Кто: частный физик
Возраст: 36
Нет. (c + v) и (c — v) — это скорости убегания света от источника в лабораторной системе отсчёта. Но никоим образом не скорости относительно источника. Вы так и не поняли разницы?
Уважаемый zam справедливо утверждает, что скорость света относительно наблюдается останется константой, тут с ним не поспоришь.
Но проблема СТО выражается в другом. В природе (реальности) нет никаких ИСО и наблюдателей. А есть как раз скорость убегания фотона от источника. В одном случае она будет больше относительной скорости света, а в другом случае меньше относительной скорости света.
Но наблюдаемая относительная скорость света будет константой . Это вытекает из того, что фотон безмассовая частица (или с очень маленькой массой, которую мы когда-либо видели) и он в априори летит с максимальной скоростью с которой ему позволяет лететь среда приблизительно 300 000 км/сек.
Поэтому эксперимент Саньяка, как раз показывает, что математика СТО отлично работает, но фундаментально фотоны на других скоростях летают. СТО физической сути процессов не отражает.

#63552 Fedor :В файле 63468 полушутливо, полусерьезно я поставил zam-у несколько неудобных вопросов, над которыми ему придется поломать голову, если захочет отвечать.
Ваши вопросы никаких сложностей не вызывают.
Вопрос с результатами экспериментов Саньяка далеко не простой.
Простой.
Во вступительном тексте я предложил мысленный эксперимент с инерциальной системой отсчета, которая является аналогом интерферометра Саньяка. Система эта состоит из двух стержней, между концами которых расположен источник фотонов, а на других концах размещены два секундомера. Такая конструкция движется со скоростью v относительно неподвижной системы отсчета. Источник света одновременно излучает в противоположные стороны фотоны, длительность полета которых регистрируют секундомеры, включаясь в момент излучения и выключаясь в момент регистрации их прихода к секундомерам. На мой взгляд, такой эксперимент может подтвердить или опровергнет справедливость постулата о постоянстве скорости в инерциальных системах отсчета.
Подтверждает.
Я привел некоторые доказательства того, что принцип постоянства скорости света в таком эксперименте не выполнится так же, как это было в экспериментах Саньяка.
Не привели.
Zam выполнил решения такой задачи в рамках СТО с использованием двух инерциальных систем отсчета – неподвижной и движущейся. В решениях он использовал преобразование Лоренца для времени t=Г(t’ –vx’/c2). Здесь символ Г означает лоренц-фактор. Результат его решения в лабораторной системе отсчета изложен в файле 63295. В его представлении одновременно излученные фотоны в системе отсчета источника излучения в лабораторной системе отсчета испускаются не одновременно.
Нет. Фотоны излучаются одновременно в любой системе отсчёта (они же из одного места излучаются).
Точнее, регистрирующие их старт секундомеры запускаются не одновременно.
Вот это правильно. В лабораторной системе отсчёта секундомеры включаются не одновременно.
Тем не менее, преобразования Лоренца дают одновременный приход фотонов к секундомерам.
Нет. В лабораторной системе отсчёта ыфотоны к секундомерам приходят не одновременно.
Результат рассмотрения такого эксперимента с точки зрения движущейся системы отсчета, как и ожидалось, также оказался одновременным.
Нет. Единственное, что совпало при решении задачи двумя способами — это показания секундомеров.
Согласно расчетам zam-a, времена запуска секундомеров оказываются разными tp1= -ГvL/c2и, соответственно tp2= +ГvL/c2. Вычисляя разность результатов формул преобразования времени для моментов прибытия фотонов к секундомерам, zam получил равенство времен прибытия фотонов к местам их регистрации.
Нет. Я этого не получил. Зачем вы выдумываете? В решении чётко написаны моменты времени прихода фотоноы к секундомерам (моменты остановки секундомеров):
\(t_{S1}=\gamma (t_{S1}'-\frac{vx_{S1}'}{c^2})=\gamma (\frac{L}{c}-\frac{vL}{c^2}) \\t_{S2}=\gamma (t_{S2}'-\frac{vx_{S2}'}{c^2})=\gamma (\frac{L}{c}+\frac{vL}{c^2})\)
Разве tS1 равно tS2 ?
Решение это выполнено без связи с реальными условиями возможного эксперимента, поэтому его результат не соответствует действительности.
Нет. Решение полностью соответствует реальными условиями возможного эксперимента.
Ниже я демонстрирую это.
- Начну с результатов, которые могут быть получены в условиях справедливости классической механики. В классической механике скорость света в лабораторной (неподвижной) системе отсчета равна c. Относительно движущихся систем отсчета свет распространяется с учетом их скорости и скорости света в лабораторной системе отсчета. Таким образом, при распространении света в одном направлении с системой отсчета его скорость относительно этой системы равна c-v. В случае встречных направлений движения системы и света их относительная скорость складывается c+v. Поэтому на преодоление участка длиной L в зависимости от направления распространения свет тратит время t1 = L/(c–v) или t2= L/(c+v) и такие результаты должны зафиксировать расположенные на концах стержней секундомеры. При этом в классической механике разность времен полета фотонов оказывается равной t1– t2=2Lv/(c2-v2). Примерно такой результат Сайняк получил в экспериментах на его интерферометре.
- Далее решим эту задачу, предполагая справедливость СТО. Следует рассмотреть два варианта: с точки зрения лабораторной системы отсчета и с точки зрения связанной движением источника света системой.
В системе отсчета источника согласно с СТО свет распространяется со скоростью с. Длину стержня он проходит за время t=L/c независимо от направления распространения. Следует помнить, что в системе отсчета источника ход времени одинаков на всем протяжении пространства. Поэтому времена пуска секундомеров совпадают с временем запуска фотонов.
Теперь рассмотрим процесс движения фотонов в лабораторной системе отсчета. Для преобразования времени в этой системе используем формулу преобразований Лоренца
t=Г(t’ – vx’/c2), (1)
в которой Г =1/(1-v2/c2)1/2. Формула (1) является преобразованием для случая, когда направление скорости системы отсчета совпадает с направлением скорости света. Если скорость света имеет противоположное направление, то знак минус в формуле (1) заменяется знаком плюс.
Заметим, что момент старта фотонов соответствует значениям t’=0 и x’=0. В этот момент t1=t2 =0. Положения секундомеров при этом соответствуют x1’ =L и x2’ =-L. Подставляя их в формулу (1), получим:
t1L=Г(L/c– vL/c2) (2)
t2L=Г(L/c + vL/c2), (3)
в которых tL1 и tL2 означают времена прихода световых сигналов к соответствующим секундомерам.
Заметим, что эти значения определяют времена пролета фотонов от момента старта до момента прихода к секундомеру. При этом разность в длительности полетов фотонов равно t2L– t1L= 2ГLv/c2, величина которой совпадает с разностью в расчетах, получаемых в предположении выполнимости классической механики.
В расчетах № 63295 zam утверждает, в лабораторной системе отсчета времена включения секундомеров отличаются от момента излучения фотонов источником. Он подтверждает это соответствующими подстановками в формулу (1) числовых значений t’ и x’ в местах расположения секундомеров и вычислением времен их включения в лабораторной системе отсчета. После чего из полученных ранее значений t2Lи t1Lвычитает значения времен включения секундомеров, объявляя полученные результаты промежутком времени между моментами пуска и выключения секундомеров. Они оказываются равными и совпадающими с временами, полученными при решении задачи в системе отсчета источника.
Zam неправ при интерпретации полученных результатов. В данной задаче мы имеем две системы отсчета, в которых одни и те же секундомеры одновременно используются для измерений. В системе отсчета движущегося источника излучения они включаются одновременно. Заметим, что в момент их включения показание времени в них – нуль. С показания нуль секундомеры начинают счет независимо от системы отсчета, в которой рассматривается их работа. И это показание включается в момент излучения фотонов.
До сих пор всё на удивление логично и строго.
При этом времена пуска в обеих системах отсчета совпадают и равны нулю,
А вот это неправильно. Они не равны нулю и не совпадают. Координаты событий пуска секундомеров следует рассчитывать по преобразованиям Лоренца, точно так же, как и координаты останова секундомеров.
а времена регистрации прихода сигналов определяются формулами (2) и (3) в лабораторной системе отсчета. Они оказываются разными и величина их разности совпадает с величиной разности, полученной при решении задачи в предположении справедливости классической механики.
N.B. Полученная zam-ом задержка во включении секундомеров действительно является результатом преобразования Лоренца, но она же является свидетельством противоречивости преобразований, так как одна и та же формула при использовании ее в другой системе отсчета дает другой результат измерения одного и того же процесса.
Результаты измерения продолжительности некоторого процесса зависят от выбора системы отсчёта. Это не противоречие, а прямое следствие второго постулата СТО.
N.B2.
Итак, о чем говорят результаты расчетов.
- Имеет место различия в расчетах показаний секундомеров при использовании преобразований Лоренца в разных системах отсчета с учетом реальности момента включения секундомеров. Результаты расчетов показывают, что скорость света не одинакова в лабораторной и движущейся системах отсчета.
Нет. Результаты расчета показаний секундомеров одинаковы.
- Результаты расчетов времен движения фотонов между источником и секундомерами и моментов их прибытия к месту регистрации в лабораторной системе отсчета совпадают в СТО и классической механике.
По классике показания секундомеров разные (вы сами это показали выше). ПО СТО — показания одинаковы. Природа согласна с СТО.
- Кроме того, чтобы избежать бестолковых споров по поводу моментов включения и выключения секундомеров должен заметить, что главным является не времена регистрации, а длительность времени, затраченное фотоном на полет между источником и секундомером. Именно эта длительность определяет временную разность по приходу фотонов к секундомерам и она определяется формулами (2) и (3).
Вы, пожалуй, первый встреченный мною человек, который не понимает следующего. Чтобы измерить время прохождения бегуном дистанции следует включить секундомер одновременно со стартом бегуна и выключить секундомер одновременно с финишем бегуна.

#63621 zam :#63552 Fedor :
Я привел некоторые доказательства того, что принцип постоянства скорости света в таком эксперименте не выполнится так же, как это было в экспериментах Саньяка.
Не привели.
Вы не поняли того, что я приводил.
Тем не менее, преобразования Лоренца дают одновременный приход фотонов к секундомерам.
Нет. В лабораторной системе отсчёта ыфотоны к секундомерам приходят не одновременно.
Вы перепутали неподвижную лабораторную систему с движущейся системой, которую называете лабораторной. В ваших записях формул преобразований система К’ вместе с источником является неподвижной. Движущейся оказывается система с нештрихованными символами.
Согласно расчетам zam-a, времена запуска секундомеров оказываются разными tp1= -ГvL/c2и, соответственно tp2= +ГvL/c2. Вычисляя разность результатов формул преобразования времени для моментов прибытия фотонов к секундомерам, zam получил равенство времен прибытия фотонов к местам их регистрации.
Нет. Я этого не получил. Зачем вы выдумываете? В решении чётко написаны моменты времени прихода фотоноы к секундомерам (моменты остановки секундомеров):
\(t_{S1}=\gamma (t_{S1}'-\frac{vx_{S1}'}{c^2})=\gamma (\frac{L}{c}-\frac{vL}{c^2}) \\t_{S2}=\gamma (t_{S2}'-\frac{vx_{S2}'}{c^2})=\gamma (\frac{L}{c}+\frac{vL}{c^2})\)
Разве tS1 равно tS2 ?
Да, здесь я неудачно выразился. Хотел сказать, что затраченные на полеты фотонов времена оказались равными.
Ниже я демонстрирую это.
Заметим, что момент старта фотонов соответствует значениям t’=0 и x’=0. В этот момент t1=t2 =0. Положения секундомеров при этом соответствуют x1’ =L и x2’ =-L. Подставляя их в формулу (1), получим:
t1L=Г(L/c– vL/c2) (2)
t2L=Г(L/c + vL/c2), (3)
в которых tL1 и tL2 означают времена прихода световых сигналов к соответствующим секундомерам.
Заметим, что эти значения определяют времена пролета фотонов от момента старта до момента прихода к секундомеру. При этом разность в длительности полетов фотонов равно t2L– t1L= 2ГLv/c2, величина которой совпадает с разностью в расчетах, получаемых в предположении выполнимости классической механики.
Zam неправ при интерпретации полученных результатов. В данной задаче мы имеем две системы отсчета, в которых одни и те же секундомеры одновременно используются для измерений. В системе отсчета движущегося источника излучения они включаются одновременно. Заметим, что в момент их включения показание времени в них – нуль. С показания нуль секундомеры начинают счет независимо от системы отсчета, в которой рассматривается их работа. И это показание включается в момент излучения фотонов.
До сих пор всё на удивление логично и строго.
При этом времена пуска в обеих системах отсчета совпадают и равны нулю,
А вот это неправильно. Они не равны нулю и не совпадают. Координаты событий пуска секундомеров следует рассчитывать по преобразованиям Лоренца, точно так же, как и координаты останова секундомеров.
Здесь под словом «пуск» я имел в виду момент старта фотонов.
а времена регистрации прихода сигналов определяются формулами (2) и (3) в лабораторной системе отсчета. Они оказываются разными и величина их разности совпадает с величиной разности, полученной при решении задачи в предположении справедливости классической механики.
N.B2.
Итак, о чем говорят результаты расчетов.
- Имеет место различия в расчетах показаний секундомеров при использовании преобразований Лоренца в разных системах отсчета с учетом реальности момента включения секундомеров. Результаты расчетов показывают, что скорость света не одинакова в лабораторной и движущейся системах отсчета.
Нет. Результаты расчета показаний секундомеров одинаковы.
Результаты расчета показаний секундомеров одинаковы, а скорость света в обоих направлениях не одинакова. Это и есть главный искомый результат мысленного эксперимента!
- Результаты расчетов времен движения фотонов между источником и секундомерами и моментов их прибытия к месту регистрации в лабораторной системе отсчета совпадают в СТО и классической механике.
По классике показания секундомеров разные (вы сами это показали выше). ПО СТО — показания одинаковы. Природа согласна с СТО.
ВЫ так и не поняли цели данного мысленного эксперимента и его результатов.
Что показали эксперименты Саньяка? Они показали, что скорость света в системе движущегося источника зависит от скорости источника и направления распространения света. Другими словами эксперименты Саньяка показали, что постулат Эйнштейна о постоянстве скорости света в его движущейся системе отсчета не выполняется.
Мой мысленный эксперимент, надеюсь, я могу его так назвать, продемонстрировал тот же результат в инерциальных системах отсчета. Длительность времен полетов фотонов от одного конца стержня до другого конца оказалась разной при их распространении в разных направлениях относительно движущегося источника света.
Длительность этих времен определяется формулами
t1L=Г(L/c– vL/c2) (2)
t2L=Г(L/c + vL/c2) (3)
Разделив длину стержня на эти времена, вы получаете разную скорость распространения фотонов вдоль стержня. Вот это и есть главный результат мысленного эксперимента. Он для этого и задумывался. Этот эксперимент, проведенный в условиях инерциальных систем отсчета показал, что величина скорости света в этих системах зависит от скорости системы и направления распространения света в движущейся системе отсчета.
Должен заметить, что для получения такого результата секундомеры и их показания не потребовались, поэтому все другие расчеты, связанные с их моментами пуска и выключения никакого значения не имеют. Вот это и отражено в приведенном ниже замечании.
- Кроме того, чтобы избежать бестолковых споров по поводу моментов включения и выключения секундомеров должен заметить, что главным является не времена регистрации, а длительность времени, затраченное фотоном на полет между источником и секундомером. Именно эта длительность определяет временную разность по приходу фотонов к секундомерам и она определяется формулами (2) и (3).
Вы, пожалуй, первый встреченный мною человек, который не понимает следующего. Чтобы измерить время прохождения бегуном дистанции следует включить секундомер одновременно со стартом бегуна и выключить секундомер одновременно с финишем бегуна.
Оказывается, если имеешь нужную формулу, то можно обойтись и без секундомеров, а в случаях с бегунами, чтобы узнать, кто бежит быстрее, достаточно увидеть, кто будет первым на финише.
отредактировал(а) Fedor: 2024-06-11 07:26 GMT

#63645 Fedor :#63621 zam :#63552 Fedor :Я привел некоторые доказательства того, что принцип постоянства скорости света в таком эксперименте не выполнится так же, как это было в экспериментах Саньяка.
Не привели.
Вы не поняли того, что я приводил.
Прекрасно понял. Вы привели набор безграмотных утверждений. Это доказательством не является.
Тем не менее, преобразования Лоренца дают одновременный приход фотонов к секундомерам.
Нет. В лабораторной системе отсчёта фотоны к секундомерам приходят не одновременно.
Вы перепутали неподвижную лабораторную систему с движущейся системой, которую называете лабораторной.
Как их можно перепутать? Из двух исо мы любую можем обозвать неподвижной. Другая при этом автоматически становится движущейся.
В ваших записях формул преобразований система К’ вместе с источником является неподвижной. Движущейся оказывается система с нештрихованными символами.
И что? От этого формулы портятся?
Согласно расчетам zam-a, времена запуска секундомеров оказываются разными tp1= -ГvL/c2и, соответственно tp2= +ГvL/c2. Вычисляя разность результатов формул преобразования времени для моментов прибытия фотонов к секундомерам, zam получил равенство времен прибытия фотонов к местам их регистрации.
Нет. Я этого не получил. Зачем вы выдумываете? В решении чётко написаны моменты времени прихода фотоноы к секундомерам (моменты остановки секундомеров):
\(t_{S1}=\gamma (t_{S1}'-\frac{vx_{S1}'}{c^2})=\gamma (\frac{L}{c}-\frac{vL}{c^2}) \\t_{S2}=\gamma (t_{S2}'-\frac{vx_{S2}'}{c^2})=\gamma (\frac{L}{c}+\frac{vL}{c^2})\)
Разве tS1 равно tS2 ?
Да, здесь я неудачно выразился. Хотел сказать, что затраченные на полеты фотонов времена оказались равными.
И опять неправильно. Затраченные на полёты фотонов времена оказальсь разными: \(t_{S1}-t_0\neq t_{S2}-t_0\), потому что \(t_{S1}\neq t_{S2}\) . Фотоны «вперёд» и «назад» стартуют одновременно, а финишируют не одновременно.
При этом времена пуска в обеих системах отсчета совпадают и равны нулю,
А вот это неправильно. Они не равны нулю и не совпадают. Координаты событий пуска секундомеров следует рассчитывать по преобразованиям Лоренца, точно так же, как и координаты останова секундомеров.
Здесь под словом «пуск» я имел в виду момент старта фотонов.
Это же разные события — старт фотонов и пуск секундомеров!
Нет. Результаты расчета показаний секундомеров одинаковы.
Результаты расчета показаний секундомеров одинаковы, а скорость света в обоих направлениях не одинакова. Это и есть главный искомый результат мысленного эксперимента!
И скорость света в обоих направлениях одинакова. Это же постулат, на основе которых выведены преобразования Лоренца, которые и использованы в решениях задачи.
Хотите проверить? Поделите проходимые фотонами пути на времена, затраченные фотонами на прохождение этих путей. Что получится?
Что показали эксперименты Саньяка? Они показали, что скорость света в системе движущегося источника зависит от скорости источника и направления распространения света.
Правильно.
Другими словами эксперименты Саньяка показали, что постулат Эйнштейна о постоянстве скорости света в его движущейся системе отсчета не выполняется.
Вики: https://ru.wikipedia.org/wiki/Специальная_теория_относительности#Постулаты_СТО https://ru.wikipedia.org/wiki/Специальная_теория_относительности#Постулаты_СТО. Там написано:
Постулат 2 (принцип постоянства скорости света). Скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга [то есть, в ИСО]
Система движущегося источника (вращающегося стола) не является инерциальной.
Вы опять промахнулись со своей критикой.
Мой мысленный эксперимент, надеюсь, я могу его так назвать, продемонстрировал тот же результат в инерциальных системах отсчета. Длительность времен полетов фотонов от одного конца стержня до другого конца оказалась разной при их распространении в разных направлениях относительно движущегося источника света.
Длительность этих времен определяется формулами
t1L=Г(L/c– vL/c2) (2)
t2L=Г(L/c + vL/c2) (3)
Не от одного конца до другого, а от середины к разным концам, но это мелочи.
Это времена полёта фотонов в лабораторной системе отсчёта, а не в системе источника света (стержня). Поэтому и делить на эти времена не L (путь фотона в системе источника), а пути фотона в лабораторной системе отсчёта. Поделите и убедитесь, что опять получается та самая «c».
Вот это и есть главный результат мысленного эксперимента.
Главный результат вашего мысленного эксперимента состоит в том, что вы не умеете выполнять мысленные эксперименты.
Должен заметить, что для получения такого результата секундомеры и их показания не потребовались, поэтому все другие расчеты, связанные с их моментами пуска и выключения никакого значения не имеют.
Согласен. Без секундомеров было бы в два раза короче. А результат — тот же.
Вы, пожалуй, первый встреченный мною человек, который не понимает следующего. Чтобы измерить время прохождения бегуном дистанции следует включить секундомер одновременно со стартом бегуна и выключить секундомер одновременно с финишем бегуна.
Оказывается, если имеешь нужную формулу, то можно обойтись и без секундомеров,
Нужно ещё уметь пользоваться формулами.
а в случаях с бегунами, чтобы узнать, кто бежит быстрее, достаточно увидеть, кто будет первым на финише.
Только в том случае, если они стартуют одновременно. А вот у лыжников очень часто проводят соревнования с раздельным стартом (спортсмены стартуют с интервалом в 30 секунд). Тут уж без секундомера не обойтись.

#63669 zam :#63645 Fedor :Что показали эксперименты Саньяка? Они показали, что скорость света в системе движущегося источника зависит от скорости источника и направления распространения света.
Правильно.
Другими словами эксперименты Саньяка показали, что постулат Эйнштейна о постоянстве скорости света в его движущейся системе отсчета не выполняется.
Система движущегося источника (вращающегося стола) не является инерциальной.
Вы опять промахнулись со своей критикой.
Я не критикую, я отмечаю, что в его движущейся системе постулат Эйнштейна не работает. Причины не обсуждаю.
Мой мысленный эксперимент, надеюсь, я могу его так назвать, продемонстрировал тот же результат в инерциальных системах отсчета. Длительность времен полетов фотонов от одного конца стержня до другого конца оказалась разной при их распространении в разных направлениях относительно движущегося источника света.
Длительность этих времен определяется формулами
t1L=Г(L/c– vL/c2) (2)
t2L=Г(L/c + vL/c2) (3)
Не от одного конца до другого, а от середины к разным концам, но это мелочи.
Это времена полёта фотонов в лабораторной системе отсчёта, а не в системе источника света (стержня). Поэтому и делить на эти времена не L (путь фотона в системе источника), а пути фотона в лабораторной системе отсчёта. Поделите и убедитесь, что опять получается та самая «c».
В вашем способе решения задачи лабораторной (неподвижной) системой отсчета является система источника, в которой длина стержня равна L. Это вносит путаницу в понимание полученного результата. Я предлагаю рассмотреть задачу с традиционным видом преобразований, в которых штрихуется движущаяся система отсчета. В этом случае источник движется так же, как у Саньяка.
Для начала повторю то, что считаю очевидным и не подлежащим сомнению. Есть инерционная система отсчета с движущимся источником и двумя стержнями длиной L. Символы физических величин этой системы обозначаем штрихами. В неподвижной (лабораторной) системе отсчета скорость света равна с. В лабораторной СО относительно источника скорость света зависит от направления распространения и имеет величины c+v– в случае встречного движения и c-v в случае совпадения направлений движения света и источника. Следовательно, в лабораторной СО длину стержней свет одолеет за времена t1s=L/(c-v), t2s=L/(c+v). Итак, в лабораторной СО длительности времени на движения фотонов от одного конца стержня до другого конца оказываются разными. Это означает, что излученные с одной волновой фазой фотоны, к финишу придут с разной фазой. В этом результате сомневаться бессмысленно. Заметим, что такую же разность во временах полета фотонов получил Саньяк.
Теперь воспользуемся преобразованиями Лоренца. Замечу сразу, если результат преобразований не совпадет с результатом, полученным феноменологическим путем, то преобразования врут. В случае совпадения результатов, то можно будет полагать, что преобразования правильно преобразуют координаты пространства и времени между ИСО, хотя в других случаях может проявиться их ошибочность..
Далее используем следующие выражения для преобразований
t ’ = Г(t–vx/c2); x’=Г(x-vt), (1)
в которых нештрихованные символы относятся к неподвижной СО. Начало процесса соответствует t’=t=0; x’=x=0. t’ – время в СО источника. Координаты концов стержней x1=L, x2=-L. В СО источника время одинаково во всем пространстве. Подставляя значения x1 и x2 в формулу преобразования времени для момента t'=0 получим времена момента излучения на концах стержней t1L=vL/c2и t2L= -vL/c2в лабораторной системе отсчета.
Далее используем формулу преобразования времени для определения времен финиша пути фотонов. Пространственные координаты концов стержней в лабораторной системе нам известны. Неизвестными являются времена финиша t1F и t2F. Их мы найдем, зная пройденный в лабораторной системе путь от старта до конца стержня каждым фотоном
L 1 =ct1 =L+vt1, t1 =L/(c-v)
L 2 =ct2=L-vt2, t2=L/(c+v).
Финишное время для каждого фотона состоит из суммы стартового времени и времени движения фотона с момента старта до момента финиша.
t 1F =t1L+t1 =L/(c-v)+vL/c2
t 2F =t2L+t2 =L/(c+v)-vL/c2.
Используя формулу преобразования времени, находим
t ’1F=Г(L/(c-v)+vL/c2-vL/c2) = ГL/(c-v)
t’ 2F=Г(L/(c+v)-vL/c2+vL/c2) =ГL/(c+v).
Таким образом, при скорости света в лабораторной СО равной с, в системе отсчета источника фотоны приходят к финишу в разное время. Это означает, что скорость света в СО источника не равна с.
отредактировал(а) Fedor: 2024-06-12 15:36 GMT

#63702 Fedor :Система движущегося источника (вращающегося стола) не является инерциальной.
Вы опять промахнулись со своей критикой.
Я не критикую, я отмечаю, что в его движущейся системе постулат Эйнштейна не работает. Причины не обсуждаю.
Вы именно критикуете.
Постулат Эйнштейна к вращающимся системам отсчёта не относится. В геоцентрической (вращающейся) системе отсчёта даже далёкие звёзды двигаются со сверхсветовыми скоростями (сколько уже раз я вам про это рассказывал?). Чего уж тут от света ожидать?
Это времена полёта фотонов в лабораторной системе отсчёта, а не в системе источника света (стержня). Поэтому и делить на эти времена не L (путь фотона в системе источника), а пути фотона в лабораторной системе отсчёта. Поделите и убедитесь, что опять получается та самая «c».
В вашем способе решения задачи лабораторной (неподвижной) системой отсчета является система источника, в которой длина стержня равна L.
Совершенно не важно, какую систему считать неподвижной.
Буквой L обозначена собственная длина стержня. А собственные величины — это величины инвариантные, от выбора системы отсчёта не зависят. Конечно, лучше было бы использовать обозначение L0 (вроде, я уже про это писал).
Это вносит путаницу в понимание полученного результата. Я предлагаю рассмотреть задачу с традиционным видом преобразований, в которых штрихуется движущаяся система отсчета. В этом случае источник движется так же, как у Саньяка.
Для начала повторю то, что считаю очевидным и не подлежащим сомнению. Есть инерционная система отсчета с движущимся источником и двумя стержнями длиной L. Символы физических величин этой системы обозначаем штрихами. В неподвижной (лабораторной) системе отсчета скорость света равна с. В лабораторной СО относительно источника скорость света зависит от направления распространения и имеет величины c+v– в случае встречного движения и c-v в случае совпадения направлений движения света и источника.
Неправильно. Это не относительные скорости. (c + v) — это скорость убегания света от источника в направлении, противоположном направлению движения мсточника. (c - v) — это скорость убегания света от источника в направлении, попутном направлению движения мсточника.
Следовательно, в лабораторной СО длину стержней свет одолеет за времена t1s=L/(c-v), t2s=L/(c+v).
Забыли гамму: \(t_{1S}=\frac{L}{\gamma \left ( c-v \right )} \\t_{2S}=\frac{L}{\gamma \left ( c+v \right )} \) .
Итак, в лабораторной СО длительности времени на движения фотонов от одного конца стержня до другого конца оказываются разными. Это означает, что излученные с одной волновой фазой фотоны, к финишу придут с разной фазой. В этом результате сомневаться бессмысленно. Заметим, что такую же разность во временах полета фотонов получил Саньяк.
Теперь воспользуемся преобразованиями Лоренца. Замечу сразу, если результат преобразований не совпадет с результатом, полученным феноменологическим путем, то преобразования врут.
Каким-каким путём?
В случае совпадения результатов, то можно будет полагать, что преобразования правильно преобразуют координаты пространства и времени между ИСО, хотя в других случаях может проявиться их ошибочность..
Далее используем следующие выражения для преобразований
t ’ = Г(t–vx/c2); x’=Г(x-vt), (1)
в которых нештрихованные символы относятся к неподвижной СО. Начало процесса соответствует t’=t=0; x’=x=0. t’ – время в СО источника. Координаты концов стержней x1=L, x2=-L.
Нет. \(x_1=\frac{L}{\gamma };\; x_2=-\frac{L}{\gamma } \) .
В СО источника время одинаково во всем пространстве.
Бессмысленная фраза.
Подставляя значения x1 и x2 в формулу преобразования времени для момента t'=0 получим времена момента излучения на концах стержней t1L=vL/c2и t2L= -vL/c2в лабораторной системе отсчета.
Не понял. У вас же источник света в середине стержня, а не на концах.
Далее используем формулу преобразования времени для определения времен финиша пути фотонов. Пространственные координаты концов стержней в лабораторной системе нам известны. Неизвестными являются времена финиша t1F и t2F. Их мы найдем, зная пройденный в лабораторной системе путь от старта до конца стержня каждым фотоном
L 1 =ct1 =L+vt1, t1 =L/(c-v)
L 2 =ct2=L-vt2, t2=L/(c+v).
Финишное время для каждого фотона состоит из суммы стартового времени и времени движения фотона с момента старта до момента финиша.
t 1F =t1L+t1 =L/(c-v)+vL/c2
t 2F =t2L+t2 =L/(c+v)-vL/c2.
Используя формулу преобразования времени, находим
t ’1F=Г(L/(c-v)+vL/c2-vL/c2) = ГL/(c-v)
t’ 2F=Г(L/(c+v)-vL/c2+vL/c2) =ГL/(c+v).
Таким образом, при скорости света в лабораторной СО равной с, в системе отсчета источника фотоны приходят к финишу в разное время. Это означает, что скорость света в СО источника не равна с.
Вы как-то по ходу дела изменили условия задачи. Давайте вы их аккуратно запишете (уже без секундомеров). А потом посмотрим, что получается.

#63716 zam :#63702 Fedor :В вашем способе решения задачи лабораторной (неподвижной) системой отсчета является система источника, в которой длина стержня равна L.
Совершенно не важно, какую систему считать неподвижной.
Не важно, если задача решается правильно и правильно интерпретируются результаты решения.
Буквой L обозначена собственная длина стержня. А собственные величины — это величины инвариантные, от выбора системы отсчёта не зависят. Конечно, лучше было бы использовать обозначение L0 (вроде, я уже про это писал).
Это вносит путаницу в понимание полученного результата. Я предлагаю рассмотреть задачу с традиционным видом преобразований, в которых штрихуется движущаяся система отсчета. В этом случае источник движется так же, как у Саньяка.
Для начала повторю то, что считаю очевидным и не подлежащим сомнению. Есть инерционная система отсчета с движущимся источником и двумя стержнями длиной L. Символы физических величин этой системы обозначаем штрихами. В неподвижной (лабораторной) системе отсчета скорость света равна с. В лабораторной СО относительно источника скорость света зависит от направления распространения и имеет величины c+v– в случае встречного движения и c-v в случае совпадения направлений движения света и источника.
Неправильно. Это не относительные скорости. (c + v) — это скорость убегания света от источника в направлении, противоположном направлению движения мсточника. (c - v) — это скорость убегания света от источника в направлении, попутном направлению движения мсточника.
Словосочетания «скорость относительно источника» и «скорость убегания от источника» имеют одинаковый смысл.
Следовательно, в лабораторной СО длину стержней свет одолеет за времена t1s=L/(c-v), t2s=L/(c+v).
Забыли гамму: \(t_{1S}=\frac{L}{\gamma \left ( c-v \right )} \\t_{2S}=\frac{L}{\gamma \left ( c+v \right )} \) .
Результат моих рассуждений не зависит от длины стержня, в какой бы СО я его не задавал.
Итак, в лабораторной СО длительности времени на движения фотонов от одного конца стержня до другого конца оказываются разными. Это означает, что излученные с одной волновой фазой фотоны, к финишу придут с разной фазой. В этом результате сомневаться бессмысленно. Заметим, что такую же разность во временах полета фотонов получил Саньяк.
Теперь воспользуемся преобразованиями Лоренца. Замечу сразу, если результат преобразований не совпадет с результатом, полученным феноменологическим путем, то преобразования врут.
Каким-каким путём?
Аналитически, без использования строгих математических выкладок.
В случае совпадения результатов, то можно будет полагать, что преобразования правильно преобразуют координаты пространства и времени между ИСО, хотя в других случаях может проявиться их ошибочность..
Далее используем следующие выражения для преобразований
t ’ = Г(t–vx/c2); x’=Г(x-vt), (1)
в которых нештрихованные символы относятся к неподвижной СО. Начало процесса соответствует t’=t=0; x’=x=0. t’ – время в СО источника. Координаты концов стержней x1=L, x2=-L.
Нет. \(x_1=\frac{L}{\gamma };\; x_2=-\frac{L}{\gamma } \) .
В лабораторной (неподвижной) системе отсчета длину стержня я назначаю величиной L.
В СО источника время одинаково во всем пространстве.
Бессмысленная фраза.
Эта фраза несет совершенно определенный смысл. Для тех, кто не понял, поясню. В любой инерциальной системе отсчета ход времени не зависит от пространственной координаты. Это означает, если в точке x=0 время t=0, то и в точке x=L время t=0.
Подставляя значения x1 и x2 в формулу преобразования времени для момента t'=0 получим времена момента излучения на концах стержней t1L=vL/c2и t2L= -vL/c2в лабораторной системе отсчета.
Не понял. У вас же источник света в середине стержня, а не на концах.
У каждого из стержней есть два конца. Источник находится в месте касания двух концов разных стержней. В данном случае получены значения времени t на других концах стержней, когда в месте нахождения источника света времена неподвижной и движущейся СО равнялись нулю.
Далее используем формулу преобразования времени для определения времен финиша пути фотонов. Пространственные координаты концов стержней в лабораторной системе нам известны. Неизвестными являются времена финиша t1F и t2F. Их мы найдем, зная пройденный в лабораторной системе путь от старта до конца стержня каждым фотоном
L 1 =ct1 =L+vt1, t1 =L/(c-v)
L 2 =ct2=L-vt2, t2=L/(c+v).
Финишное время для каждого фотона состоит из суммы стартового времени и времени движения фотона с момента старта до момента финиша.
t 1F =t1L+t1 =L/(c-v)+vL/c2
t 2F =t2L+t2 =L/(c+v)-vL/c2.
Используя формулу преобразования времени, находим
t ’1F=Г(L/(c-v)+vL/c2-vL/c2) = ГL/(c-v)
t’ 2F=Г(L/(c+v)-vL/c2+vL/c2) =ГL/(c+v).
Таким образом, при скорости света в лабораторной СО равной с, в системе отсчета источника фотоны приходят к финишу в разное время. Это означает, что скорость света в СО источника не равна с.
Вы как-то по ходу дела изменили условия задачи. Давайте вы их аккуратно запишете (уже без секундомеров). А потом посмотрим, что получается.
Решение записано аккуратно. Секундомеры при решении не использовались.

#63730 Fedor :#63716 zam :Совершенно не важно, какую систему считать неподвижной.
Не важно, если задача решается правильно и правильно интерпретируются результаты решения.
Правильно.
Буквой L обозначена собственная длина стержня. А собственные величины — это величины инвариантные, от выбора системы отсчёта не зависят. Конечно, лучше было бы использовать обозначение L0 (вроде, я уже про это писал).
Это вносит путаницу в понимание полученного результата. Я предлагаю рассмотреть задачу с традиционным видом преобразований, в которых штрихуется движущаяся система отсчета. В этом случае источник движется так же, как у Саньяка.
Хорошо. Я попробую грамотно сформулировать такую задачу.
Неправильно. Это не относительные скорости. (c + v) — это скорость убегания света от источника в направлении, противоположном направлению движения мсточника. (c - v) — это скорость убегания света от источника в направлении, попутном направлению движения мсточника.
Словосочетания «скорость относительно источника» и «скорость убегания от источника» имеют одинаковый смысл.
Нет. Скорость некоторого объекта относительно источника — это скорость данного объекта в системе отсчёта источника.
Скорость убегания одного объекта от дркгого (скорость разбегания двух объектов, скорость сближения двух объектов...) — это разница скоростей двух объектов в некоторой системе отсчёта.
Эти скорости равны в механике Ньютона-Лагранжа. То есть, там, где используются преобразования Галилея. А если используются преобразования Лоренца, то эти скорости не равны.
Теперь воспользуемся преобразованиями Лоренца. Замечу сразу, если результат преобразований не совпадет с результатом, полученным феноменологическим путем, то преобразования врут.
Каким-каким путём?
Аналитически, без использования строгих математических выкладок.
Аналитически — это как раз с использованием математических выкладок.
А феноменологически, насколько я понял, это путём смотрения на потолок и ковыряния в носу.
В СО источника время одинаково во всем пространстве.
Бессмысленная фраза.
Эта фраза несет совершенно определенный смысл. Для тех, кто не понял, поясню. В любой инерциальной системе отсчета ход времени не зависит от пространственной координаты. Это означает, если в точке x=0 время t=0, то и в точке x=L время t=0.
Ну, пускай так.
Вот как выглядит система отсчёта (картинка из книги Уилера):

Это бесконечная во все стороны решётка из метровых линеек, в узлах которой развешаны синхронизированные часы.
То, что вы странно называете «время одинаково во всем пространстве», означает, что в ИСО мы можем разместить сколько угодно и где угодно покоящихся синхронизированных часов.

#63752 zam :Хорошо. Я попробую грамотно сформулировать такую задачу.
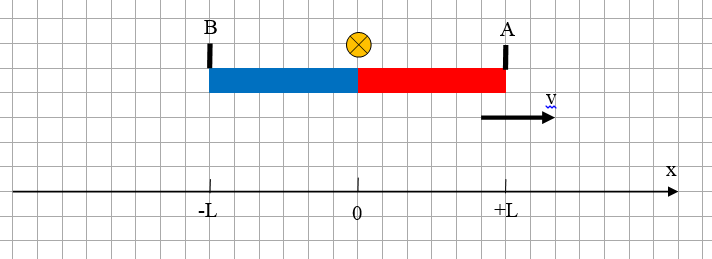
Задача сто-005
В некоторой инерциальной системе отсчёта, которую назовём лабораторной, двигаются с постоянной скоростью v два стержня, красный и синий. Результат измерения длины стержней в лабораторной системе отсчёта равен L.
Между стержнями источник света, который в некоторый момент времени (t = 0) даёт вспышку.
На концах стержней регистраторы света «А» и «В».
Требуется найти время движения фотонов от источника света к регистраторам А и В и пройденные ими пути в лабораторной ИСО и в ИСО стержней.
Решение задачи сто-005
Имеем лабораторную (условно неподвижную) ИСО, обозначение К, физические величины не штрихованы.
Имеем ИСО стержня (движущуюся), обозначение К’, физические величины штрихованы.
1. Лабораторная ИСО.
Начальное расстояние между фотоном и регистратором равно L. Скорость сближения фотона с регистратором А равна (с – v). Время движения фотона до регистратора А равно \(\Delta t_A=\frac{L}{c-v}\). Пройденный им путь \(\Delta x_A=c\Delta t_A=L\frac{c}{c-v}\) .
Скорость сближения фотона с регистратором В равна (с + v). Время движения фотона до регистратора В равно \(\Delta t_B=\frac{L}{c+v}\) . Пройденный им путь \(\Delta x_B=c\Delta t_B=L\frac{c}{c+v}\) . Имеем три события:
— событие «О», излучение фотонов: \(\left ( t_0=0,\; x_0=0 \right )\);
— событие «А», поглощение фотона регистратором А: \(\left ( t_A=\frac{L}{c-v},\; x_A=L\frac{c}{c-v} \right ) \);
— событие «В», поглощение фотона регистратором И: \(\left ( t_B=\frac{L}{c+v},\; x_B=-L\frac{c}{c+v} \right )\).
2. ИСО стержней.
В ИСО стержня длина стержней равна их собственной длине, то есть \(L_0=L'=L \).
Время движения фотонов до регистраторов равно \(\Delta t_A'=\Delta t_B'=\frac{L'}{c}=\gamma \frac{L}{c}\) .
Пройденные ими пути равны \(\Delta x_A'=\Delta x_B'=c\Delta t_A'=c\Delta t_B'=L'=\gamma L\) .
Имеем три события:
— событие «О», излучение фотонов: \(\left ( t_0'=0,\; x_0'=0 \right )\);
— событие «А», поглощение фотона регистратором А: \(\left ( t_A'=\frac{L'}{c}=\gamma \frac{L}{c},\; x_A'=L'=\gamma L \right ) \);
— событие «В», поглощение фотона регистратором В: \(\left ( t_B'=\frac{L'}{c}=\gamma \frac{L}{c},\; x_B'=-L'=-\gamma L \right ) \).
Проверим преобразования Лоренца:
\(x'=\gamma \left ( x-vt \right ) \\t'=\gamma \left ( t-\frac{vx}{c^2} \right )\)
Событие «О».
\(x_0'=\gamma \left ( x_0-vt_0 \right )=0 \\t_0'=\gamma \left ( t_0-\frac{vx_0}{c^2} \right )=0\)
Событие «А».
\(x_A'=\gamma \left ( x_A-vt_A \right )=\gamma \left ( L\frac{c}{c-v}-v\frac{L}{c-v} \right )=\gamma L \\t_A'=\gamma \left ( t_A-\frac{vx_A}{c^2} \right )=\gamma \left ( \frac{L}{c-v}-\frac{vL\frac{c}{c-v}}{c^2} \right )=\gamma \frac{L}{c}\)
Событие «В».
\(x_B'=\gamma \left ( x_B-vt_B \right )=\gamma \left ( -L\frac{c}{c+v}-v\frac{L}{c+v} \right )=-\gamma L \\t_B'=\gamma \left ( t_B-\frac{vx_B}{c^2} \right )=\gamma \left ( \frac{L}{c+v}-\frac{-vL\frac{c}{c+v}}{c^2} \right )=\gamma \frac{L}{c}\)
Всё сходится.

#63752 zam :#63730 Fedor :#63716 zam :Совершенно не важно, какую систему считать неподвижной.
Не важно, если задача решается правильно и правильно интерпретируются результаты решения.
Дело в том, что Вы эту задачу решили правильно, а результат сфальсифицировали. Поясняю.
В вашей задаче символами без штрихов физические величины системы отсчета, которая движется относительно неподвижной системы со скоростью v. СО источника у Вас неподвижна и ее символы Вы обозначаете штрихами. Событие старта фотонов в обеих системах определяется величинами
t=t’ = 0; x=x’ = 0. В этот момент на других концах стержней никаких событий не происходит. Этот момент означает начало процесса распространения фотонов в обеих системах. Заметим также, в системе без штрихов ход времени не зависит от пространственной координаты и поэтому реально момент времени старта фотонов в точке x=L время этой СО t0 =0. Ваше tP – это лишь результат преобразования, который к процессу отношения не имеет. Между тем реальный фотон прибывает в точку x' = L. Это момент финиша процесса. Координата x’ =L в вашей неподвижной СО соответствует времени t’F=L/c. Подставляя эти величины в формулу преобразования времени, Вы получаете время финиша процесса в Вашей движущейся системе, относящееся к концу стержня, к которому прилетел фотон. Итак, в этой системе отсчета событие старта соответствует t=0, x=0, событие финиша x=L, t=ts. Ваши расчеты подтвердили, что ts1 не равно ts2.
Теперь воспользуемся преобразованиями Лоренца. Замечу сразу, если результат преобразований не совпадет с результатом, полученным феноменологическим путем, то преобразования врут.
Каким-каким путём?
Аналитически, без использования строгих математических выкладок.
Аналитически — это как раз с использованием математических выкладок.
А феноменологически, насколько я понял, это путём смотрения на потолок и ковыряния в носу.
Слово феноменологически само раскрывает смысл метода – рассмотрения явления с использованием логики. И по поводу употребления этого слова, действительно, не следует ковыряться в носу.

#63756 Fedor :Дело в том, что Вы эту задачу решили правильно, а результат сфальсифицировали.
Нет.
Событие старта фотонов в обеих системах определяется величинами t=t’ = 0; x=x’ = 0. В этот момент на других концах стержней никаких событий не происходит.
В системе отсчёта стержней в этот момент включаются секундомеры. В лабораторной системе в этот момент событий нет.
Ваше tP – это лишь результат преобразования, который к процессу отношения не имеет.
У меня такой величины нет. У меня есть tP1, tP2, tР1', tР2'. Это моменты пуска секундомеров в системах отсчёта К и К'. Они имеют отношение не к процессам, а к событиям. Как и преобразования Лоренца.
Между тем реальный фотон прибывает в точку x' = L.
А другой — в точку x' = -L. А про виртуальные фотоны мы тут не говорим. Так?
Это момент финиша процесса. Координата x’ =L в вашей неподвижной СО соответствует времени t’F=L/c.
События прибытия фотонов к секундомерам имеют координаты (t' = L/c, x' = L) и (t' = L/c, x' = -L).
А координата x' = L соответствует всем моментам времени, от минус бесконечности до плюс бесконечности.
Подставляя эти величины в формулу преобразования времени, Вы получаете время финиша процесса в Вашей движущейся системе, относящееся к концу стержня, к которому прилетел фотон.
Я получаю момент прибытия фотона к секундомеру в ИСО К. Естественно, секундомер на конце стержня.
Итак, в этой системе отсчета событие старта соответствует t=0, x=0, событие финиша x=L, t=ts.
Нет. Событие финиша \(\left ( t_{S1}=\gamma\frac{L}{c} (1-\frac{v}{c}),\: \; x_{S1}=\gamma L (1-\frac{v}{c}) \right )\).
Ваши расчеты подтвердили, что ts1 не равно ts2.
Естественно. По-другому и быть не может. Один секундомер убегает от светового луча, а другой бежит ему навстречу.
Аналитически — это как раз с использованием математических выкладок.
А феноменологически, насколько я понял, это путём смотрения на потолок и ковыряния в носу.
Слово феноменологически само раскрывает смысл метода – рассмотрения явления с использованием логики. И по поводу употребления этого слова, действительно, не следует ковыряться в носу.
Математика для того и придумана, чтобы избегать логических ошибок.
Рассматривать с использованием логики — значит использовать математику.
Заменять математику пустой говорильней — вот это, по-видимому, и означает — феноменологически.
Вики: https://ru.wikipedia.org/wiki/Феноменология https://ru.wikipedia.org/wiki/Феноменология .
Цитата оттуда:
Сам термин введён Гегелем
Вполне достаточно, чтобы навсегда забыть.

#63753 zam :
Имеем лабораторную (условно неподвижную) ИСО, обозначение К, физические величины не штрихованы.
Имеем ИСО стержня (движущуюся), обозначение К’, физические величины штрихованы.
1. Лабораторная ИСО.
Начальное расстояние между фотоном и регистратором равно L. Скорость сближения фотона с регистратором А равна (с – v). Время движения фотона до регистратора А равно \(\Delta t_A=\frac{L}{c-v}\). Пройденный им путь \(\Delta x_A=c\Delta t_A=L\frac{c}{c-v}\) .
Скорость сближения фотона с регистратором В равна (с + v). Время движения фотона до регистратора В равно \(\Delta t_B=\frac{L}{c+v}\) . Пройденный им путь \(\Delta x_B=c\Delta t_B=L\frac{c}{c+v}\) . Имеем три события:
— событие «О», излучение фотонов: \(\left ( t_0=0,\; x_0=0 \right )\);
— событие «А», поглощение фотона регистратором А: \(\left ( t_A=\frac{L}{c-v},\; x_A=L\frac{c}{c-v} \right ) \);
Ошибка. Нужно последовательно использовать преобразования. Ваше tA это всего лишь длительность времени полета фотона от источника до пункта А. На момент старта процесса в точке А уже было не равное нулю время t=vxA/c2, полученное из преобразования для момента t’ =0 в точке xA, поэтому tA= L/(c-v)+ vxA/c2. По тем же причинам tB=L/(c+v)-vxB/c2.
Вот эти времена Вы должны использовать в выражении для преобразования времени.
Всё сходится.
Не сходится.
PS. Так как в таком варианте задачи «интерферометр» находится в движении, то и секундомеры движутся с ним. Включаются они одновременно с моментом пуска фотонов, а выключаются в момент прихода фотонов. Поэтому t’A = L/(c-v) и t’B = L/(c+v) – это то, что покажут секундомеры.
отредактировал(а) Fedor: 2024-06-15 09:32 GMT

#63765 zam :#63756 Fedor :
Событие старта фотонов в обеих системах определяется величинами t=t’ = 0; x=x’ = 0. В этот момент на других концах стержней никаких событий не происходит.
В системе отсчёта стержней в этот момент включаются секундомеры. В лабораторной системе в этот момент событий нет.
Ваше tP – это лишь результат преобразования, который к процессу отношения не имеет.
У меня такой величины нет. У меня есть tP1, tP2, tР1', tР2'. Это моменты пуска секундомеров в системах отсчёта К и К'. Они имеют отношение не к процессам, а к событиям. Как и преобразования Лоренца.
К событиям имеют, однако к процессам не имеют.
События прибытия фотонов к секундомерам имеют координаты (t' = L/c, x' = L) и (t' = L/c, x' = -L).
А координата x' = L соответствует всем моментам времени, от минус бесконечности до плюс бесконечности.
И все они равны t’s , так как это момент финиша фотона в СО K’.
Подставляя эти величины в формулу преобразования времени, Вы получаете время финиша процесса в Вашей движущейся системе, относящееся к концу стержня, к которому прилетел фотон.
Я получаю момент прибытия фотона к секундомеру в ИСО К. Естественно, секундомер на конце стержня.
В ИСО К секундомера нет. Он вместе со стержнем находится в ИСО K’.
Итак, в этой системе отсчета событие старта соответствует t=0, x=0, событие финиша x=L, t=ts.
Нет. Событие финиша \(\left ( t_{S1}=\gamma\frac{L}{c} (1-\frac{v}{c}),\: \; x_{S1}=\gamma L (1-\frac{v}{c}) \right )\).
Ваши расчеты подтвердили, что ts1 не равно ts2.
Естественно. По-другому и быть не может. Один секундомер убегает от светового луча, а другой бежит ему навстречу.
Но секундомеры у Вас находятся в неподвижной системе K’ и Вы им определили одинаковые показания t’S1=t’s2 =ГL/c. Но эти показания имеют весьма отдаленное отношение к временам распространения света в лабораторной системе отсчета. Там они оказываются разными.
Итак, Вы получили противоречивый результат. В неподвижной СО K’ к концам стержней фотоны приходят одновременно, а в лабораторной СО К к тем же концам стержней они приходят не одновременно. Какому результату мы должны верить? Саньяк экспериментально получил неодновременный приход фотонов. Результаты расчетов в лабораторной инерциальной системе отсчета совпали с результатами экспериментов Саньяка.
Несовпадение результатов решения задачи в разных системах отсчета говорит об ошибочности преобразований.
Слово феноменологически само раскрывает смысл метода – рассмотрения явления с использованием логики. И по поводу употребления этого слова, действительно, не следует ковыряться в носу.
Математика для того и придумана, чтобы избегать логических ошибок.
Большинство ошибок в математических расчетах является результатом логических ошибок.

#63774 Fedor :#63753 zam :Имеем лабораторную (условно неподвижную) ИСО, обозначение К, физические величины не штрихованы.
Имеем ИСО стержня (движущуюся), обозначение К’, физические величины штрихованы.
1. Лабораторная ИСО.
Начальное расстояние между фотоном и регистратором равно L. Скорость сближения фотона с регистратором А равна (с – v). Время движения фотона до регистратора А равно \(\Delta t_A=\frac{L}{c-v}\). Пройденный им путь \(\Delta x_A=c\Delta t_A=L\frac{c}{c-v}\) .
Скорость сближения фотона с регистратором В равна (с + v). Время движения фотона до регистратора В равно \(\Delta t_B=\frac{L}{c+v}\) . Пройденный им путь \(\Delta x_B=c\Delta t_B=L\frac{c}{c+v}\) . Имеем три события:
— событие «О», излучение фотонов: \(\left ( t_0=0,\; x_0=0 \right )\);
— событие «А», поглощение фотона регистратором А: \(\left ( t_A=\frac{L}{c-v},\; x_A=L\frac{c}{c-v} \right ) \);
Ошибка.
Где?
Нужно последовательно использовать преобразования.
Покажите как.
Вашеэто всего лишь длительность времени полета фотона от источника до пункта А.
t A — это момент прибытия фотона к регистратору А. Время полёта фотона — это \(\Delta t_A=t_A-t_0= t_A\) (t0 — это момент вылета фотона из источника).
На момент старта процесса в точке А уже было не равное нулю время t = vx A/c2, полученное из преобразования для момента t’ =0 в точке xA, поэтому tA= L/(c-v)+ vxA/c2. По тем же причинам tB=L/(c+v)-vxB/c2.
Что такое «момент старта процесса»? Так вы называете момент вылета фотонов? Ну, пускай. В этот момент во всех точках системы отсчёта «К» t = 0. А штрихованные величины (t') тут вообще ни при чём. Задача решается в системе отсчёта «К» (без штрихов).
Вот эти времена Вы должны использовать в выражении для преобразования времени.
Пока я решаю задачу в одной системе отсчёта, никакие преобразования (то есть, пересчёт физических величин из одной системы отсчёта в другую не нужны вообще.
Всё сходится.
Не сходится.
Что не сходится?
PS. Так как в таком варианте задачи «интерферометр» находится в движении, то и секундомеры движутся с ним. Включаются они одновременно с моментом пуска фотонов, а выключаются в момент прихода фотонов. Поэтому t’A = L/(c-v) и t’B = L/(c+v) – это то, что покажут секундомеры.
В задаче нет никакого интерферометра.
В задаче нет никаких секундомеров.
А вот диаграмма Минковского к задаче сто-005:
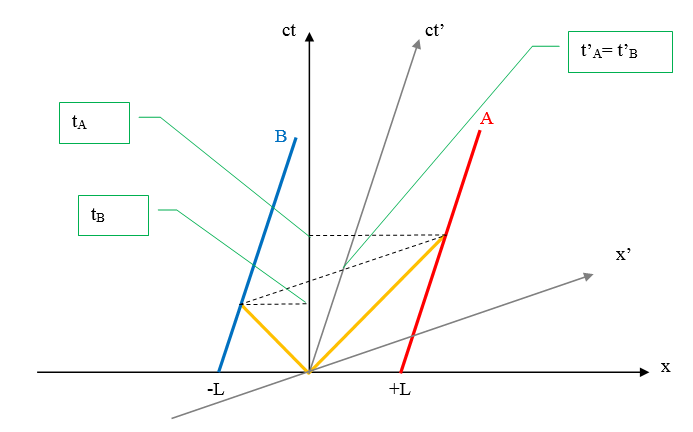
Здесь красная линия — это мировая линия правого конца красного стержня, синяя линия — мировая линия левого конца синего стержня, жёлтые линии — мировые линии фотонов. точки пересечения линий — события регистрации фотонов. Начало координат — событие испускания фотонов.
(x, ct) — система координат лабораторной системы отсчёта (К).
(x', ct') — система координат системы отсчёта стержней (К').

#63788 Fedor :В ИСО К секундомера нет. Он вместе со стержнем находится в ИСО K’.
Если «что-то» есть в одной системе отсчёта, то это «что-то» есть и во всех других системах отсчёта. Вы опять забыли, что такое система отсчёта?
Но в задаче сто-005 ( #63753 https://sfiz.ru/forums/post/63753#63753) никаких секундомеров вообще нет.
Несовпадение результатов решения задачи в разных системах отсчета говорит об ошибочности преобразований.
Результаты и не могли совпать. Потому что промежутки времени являюися величинами относительными, зависящими от выбора системы отсчёта. А вот то, что преобразования Лоренца позволяют точно перевести одни результаты в другие говорит о правильности преобразований.
А они совпали. Что говорит о правильности преобразований.
Математика для того и придумана, чтобы избегать логических ошибок.
Большинство ошибок в математических расчетах является результатом логических ошибок.
Большинство ошибок в математических расчетах является результатом неумения пользоваться математикой.
И давайте по-серьёзному.

#63934 zam :#63774 Fedor :#63753 zam :Имеем лабораторную (условно неподвижную) ИСО, обозначение К, физические величины не штрихованы.
Имеем ИСО стержня (движущуюся), обозначение К’, физические величины штрихованы.
1. Лабораторная ИСО.
Начальное расстояние между фотоном и регистратором равно L. Скорость сближения фотона с регистратором А равна (с – v). Время движения фотона до регистратора А равно \(\Delta t_A=\frac{L}{c-v}\). Пройденный им путь \(\Delta x_A=c\Delta t_A=L\frac{c}{c-v}\) .
Скорость сближения фотона с регистратором В равна (с + v). Время движения фотона до регистратора В равно \(\Delta t_B=\frac{L}{c+v}\) . Пройденный им путь \(\Delta x_B=c\Delta t_B=L\frac{c}{c+v}\) . Имеем три события:
— событие «О», излучение фотонов: \(\left ( t_0=0,\; x_0=0 \right )\);
— событие «А», поглощение фотона регистратором А: \(\left ( t_A=\frac{L}{c-v},\; x_A=L\frac{c}{c-v} \right ) \);
Ошибка.
Где?
Поясняю. Вы привели рисунок движущейся модели интерферометра в единицах измерения лабораторной системы отсчета. Однако приведенные масштабы соответствуют неподвижной конструкции интерферометра. В движущейся конструкции размер длины стержней с точки зрения лабораторной системы равен L’ =ГL. Координаты концов стержней, в которых находятся регистраторы — секундомеры Вы представили в символах неподвижной (лабораторной) СО XA, XB, tA, tB. По условию задачи регистраторы расположены на концах движущихся стержней. Их пространственные координаты равны X’A=L’, X’B= -L’. Именно относительно таких регистраторов свет распространяется со скоростями c-v и c+v, но не относительно ваших неподвижных «регистраторов», которые расположены в неподвижных точках XA и XB. Относительно движущихся регистраторов на свое движение в лабораторной СО свет потратит время tA’ =L’/(c-v) и tB’ =L’/(c+v). Вот эти значения времени покажут регистраторы, прикрепленные к концам движущихся стержней.
Вы можете определить времена старта и финиша процесса для точек X=XA и X=XB в лабораторной СО, используя преобразование Лоренца tA’ =Г(tA–vL/c2). В момент старта фотонов tA’ =0, откуда tA= vL/c2. Аналогично получим стартовое время для пункта В tB= — vL/c2. Времена финиша в шкале времени лабораторной СО вы можете получить также используя преобразование времени.

deleted
Причина: хамство, глупость, враньё, безграмотность, невежество.
ПРЕДУПРЕЖДЕНИЕ. Александр Рыбников! Сообщения в таком стиле приведут к тому, что вы разделите судьбу другого Александра (который с точкой).
отредактировал(а) zam: 2024-06-17 18:40 GMT

#63944 Александр Рыбников :deleted
Причина: хамство, глупость, враньё, безграмотность, невежество.
ПРЕДУПРЕЖДЕНИЕ. Александр Рыбников! Сообщения в таком стиле приведут к тому, что вы разделите судьбу другого Александра (который с точкой).
Уважаемый zam!
Вас очень трудно понять. Вы просто перечислили слова (хамство, глупость, враньё, безграмотность, невежество), а на самом деле физику дали Нобелевскую премию за метод совпадений.
С университетских времён я ещё помню, что нам пришлось изучать ядерную электронику (да, да Nuclear Electronics) по прямому переводу американской книги. У преподавателя курса не было приличных слов в адрес тех, кто явно тормозил этот раздел электроники в СССР.
Вы же утверждали, что знакомы с медицинской электроникой. Значит должны знать, что электронно-позитронная томография основана на прямом использовании метода совпадений
Пожалуйста, показывайте конкретно, где Вы видите то, что есть по Вашему хамство, глупость, враньё, безграмотность, невежество.
А так просто получается пшик или неустанная руководящая роль ЦК КПК.
И вообще, канадский модератор без всяких последствий обзывает меня евреем, разжигая межнациональную вражду, Александр с точкой существовал здесь ещё неделю после мата, а я оказывается во всём виноват.
Исключительно за правду в физике.

#63942 Fedor :#63934 zam :#63774 Fedor :#63753 zam :Имеем лабораторную (условно неподвижную) ИСО, обозначение К, физические величины не штрихованы.
Имеем ИСО стержня (движущуюся), обозначение К’, физические величины штрихованы.
1. Лабораторная ИСО.
Начальное расстояние между фотоном и регистратором равно L. Скорость сближения фотона с регистратором А равна (с – v). Время движения фотона до регистратора А равно \(\Delta t_A=\frac{L}{c-v}\). Пройденный им путь \(\Delta x_A=c\Delta t_A=L\frac{c}{c-v}\) .
Скорость сближения фотона с регистратором В равна (с + v). Время движения фотона до регистратора В равно \(\Delta t_B=\frac{L}{c+v}\) . Пройденный им путь \(\Delta x_B=c\Delta t_B=L\frac{c}{c+v}\) . Имеем три события:
— событие «О», излучение фотонов: \(\left ( t_0=0,\; x_0=0 \right )\);
— событие «А», поглощение фотона регистратором А: \(\left ( t_A=\frac{L}{c-v},\; x_A=L\frac{c}{c-v} \right ) \);
Ошибка.
Где?
Поясняю. Вы привели рисунок движущейся модели интерферометра в единицах измерения лабораторной системы отсчета.
Там нет никакого интерферометра. Вы знаете, что такое интерферометр? Это устройство, в котором два световых (или каких-то других, например, акустических) лучей проходят по разным путям и встречаются, чтобы сформировать интерференциаооную картину.
Однако приведенные масштабы соответствуют неподвижной конструкции интерферометра.
Какие ещё масштабы??
В движущейся конструкции размер длины стержней с точки зрения лабораторной системы равен L’ =ГL.
Вы сами предложили, чтобы результат измерения длины стержня в лабораторной систем отсчёта обозначался L (без штриха). «Я предлагаю рассмотреть задачу с традиционным видом преобразований, в которых штрихуется движущаяся система отсчета»( #63730 ).
Результат измерения длины стержня в системе отсчёта сттержня (то есть, собственная длина стержня) равняется \(L' =L_0=\gamma L\).
(В сообщении #63753 у меня опечатка, там написано \(L_0=L'=L\), но потом все выкладки верные).
Координаты концов стержней, в которых находятся регистраторы — секундомеры Вы представили в символах неподвижной (лабораторной) СО XA, XB, tA, tB.
Никаких секундомеров нет. Опять же по вашему пожеланию.
По условию задачи регистраторы расположены на концах движущихся стержней. Их пространственные координаты равны X’A=L’, X’B= -L’.
Правильно. В системе отсчёта стержней \(x_A'=L'=\gamma L, x_B'=-L'=-\gamma L\) .
Именно относительно таких регистраторов свет распространяется со скоростями c-v и c+v, но не относительно ваших неподвижных «регистраторов», которые расположены в неподвижных точках XA и XB.
Свет распространяется со скоростью «с» относительно чего угодно (второй постулат СТО)..
Относительно движущихся регистраторов на свое движение в лабораторной СО свет потратит время tA’ =L’/(c-v) и tB’ =L’/(c+v). Вот эти значения времени покажут регистраторы, прикрепленные к концам движущихся стержней.
\(\Delta t_A'=\Delta t_B'=\frac{L'}{c}=\gamma \frac{L}{c}\) .
Вы можете определить времена старта и финиша процесса
Какого процесса? У нас два процесса — полёт фотона направо и полёт фотона налево. Момент старта этого процесса \(t_0=t_0'=0\) .
отредактировал(а) zam: 2024-06-18 13:48 GMT

#63974 zam :#63942 Fedor :Поясняю. Вы привели рисунок движущейся модели интерферометра в единицах измерения лабораторной системы отсчета.
Там нет никакого интерферометра. Вы знаете, что такое интерферометр? Это устройство, в котором два световых (или каких-то других, например, акустических) лучей проходят по разным путям и встречаются, чтобы сформировать интерференциаооную картину.
Это так пятиклассник думает, что интерферометр – игрушка для получения интерференционной картинки. На самом деле это прибор для измерения разности фаз приходящих одновременно волновых сигналов. Разность фаз можно преобразовать в величину временной задержки сигналов, что мы и пытаемся сделать, используя модель интерферометра, состоящую из источника и двух стержней. Вы это прекрасно понимаете, но почему-то пытаетесь играть дурочка.
Однако приведенные масштабы соответствуют неподвижной конструкции интерферометра.
Какие ещё масштабы??
Вы это тоже понимаете.
В движущейся конструкции размер длины стержней с точки зрения лабораторной системы равен L’ =ГL.
Вы сами предложили, чтобы результат измерения длины стержня в лабораторной систем отсчёта обозначался L (без штриха). «Я предлагаю рассмотреть задачу с традиционным видом преобразований, в которых штрихуется движущаяся система отсчета»( #63730 ).
Результат измерения длины стержня в системе отсчёта сттержня (то есть, собственная длина стержня) равняется \(L' =L_0=\gamma L\).
(В сообщении #63753 у меня опечатка, там написано \(L_0=L'=L\), но потом все выкладки верные).
Координаты концов стержней, в которых находятся регистраторы — секундомеры Вы представили в символах неподвижной (лабораторной) СО XA, XB, tA, tB.
Никаких секундомеров нет. Опять же по вашему пожеланию.
Ах, да! Секундомеров нет, есть регистраторы.
По условию задачи регистраторы расположены на концах движущихся стержней. Их пространственные координаты равны X’A=L’, X’B= -L’.
Правильно. В системе отсчёта стержней \(x_A'=L'=\gamma L, x_B'=-L'=-\gamma L\) .
Именно относительно таких регистраторов свет распространяется со скоростями c-v и c+v, но не относительно ваших неподвижных «регистраторов», которые расположены в неподвижных точках XA и XB.
Свет распространяется со скоростью «с» относительно чего угодно (второй постулат СТО)..
Вы забываете, что являетесь наблюдателем лабораторной системы отсчета, с точки зрения которого свет движется относительно регистраторов со скоростями c-v и c+v. Кстати, время t’ – это время в движущейся СО с точки зрения наблюдателя, сидящего в лабораторной СО.
А вот со вторым постулатом СТО у Вас, как наблюдателя из лабораторной СО, проблемы. Не желают фотоны прибывать к регистраторам одновременно.
Относительно движущихся регистраторов на свое движение в лабораторной СО свет потратит время tA’ =L’/(c-v) и tB’ =L’/(c+v). Вот эти значения времени покажут регистраторы, прикрепленные к концам движущихся стержней.
\(\Delta t_A'=\Delta t_B'=\frac{L'}{c}=\gamma \frac{L}{c}\) .
Вы можете определить времена старта и финиша процесса
Какого процесса? У нас два процесса — полёт фотона направо и полёт фотона налево. Момент старта этого процесса \(t_0=t_0'=0\) .
Любого процесса.

#63995 Fedor :#63974 zam :Там нет никакого интерферометра. Вы знаете, что такое интерферометр? Это устройство, в котором два световых (или каких-то других, например, акустических) лучей проходят по разным путям и встречаются, чтобы сформировать интерференциаооную картину.
Это так пятиклассник думает, что интерферометр – игрушка для получения интерференционной картинки.
Нет. Даже пятиклассник так не думает (если, конечно, он не троечник).
используя модель интерферометра, состоящую из источника и двух стержней. Вы это прекрасно понимаете, но почему-то пытаетесь играть дурочка.
Интерферометр (и даже его модель) не могут состоять из источника света и двух стержней. Вы это прекрасно понимаете, но почему-то пытаетесь играть дурачка.
Однако приведенные масштабы соответствуют неподвижной конструкции интерферометра.
Какие ещё масштабы??
Вы это тоже понимаете.
Не понимаю. Приведите ссылку/цитату на учебник, где рассказывается про масштабы в СТО.
Свет распространяется со скоростью «с» относительно чего угодно (второй постулат СТО)..
Вы забываете, что являетесь наблюдателем лабораторной системы отсчета,
Я вообще не являюсь наблюдателем. Я решаю задачу, а в процессе решения ставлю смебя на место наблюдателя то в системе К (смотрю из лаборатории на пролетающий мимо меня стержень), то в системе К' (сижу на стержне).
с точки зрения которого свет движется относительно регистраторов со скоростями c-v и c+v.
Свет относительно регистраторов движется со скоростью «с». Свет относительно наблюдателя (как в системе К, так и в системе К') движется со скоростью «с».
(с — v) и (c + v) — это не скорости относительно регистраторов. Это скорости сближения регистраторов и фронта световой волны в системе отсчёта К. Эта величина не называется относительной скоростью!!! (когда же до вас это дойдёт?).
Ну опять же, хоть в школьном учебнике почитайте определение, что такое скорость движения.
Кстати, время t’ – это время в движущейся СО с точки зрения наблюдателя, сидящего в лабораторной СО.
Буковками t' у меня обозначаются моменты времени, соответствующие некоторым событиям (которые определяются нижними индексами) по часам системы К' (системы отсчёта стержней). Почему вы не читаете того, что написано в решении задачи, а подменяете своими выдумками?
А вот со вторым постулатом СТО у Вас, как наблюдателя из лабораторной СО, проблемы. Не желают фотоны прибывать к регистраторам одновременно.
В системе К' они прибывают к регистраторам одновременно.
В системе К они прибывают к регистраторам не одновременно.
Так и должно быть.
Ещё раз дать ссылку на школьный учебник? Ну, пожалуйста. Физика, 11 класс, параграф 77 «Относительность одновременности»: https://лена24.рф/Физика_11_кл_Мякишев/88.html https://лена24.рф/Физика_11_кл_Мякишев/88.html .
Относительно движущихся регистраторов на свое движение в лабораторной СО свет потратит время tA’ =L’/(c-v) и tB’ =L’/(c+v). Вот эти значения времени покажут регистраторы, прикрепленные к концам движущихся стержней.
Ничего они не покажут. Это не секундомеры.
Промежутки времени от вспышки лампы до попадания света в регистраторы вот какие:
— в системе К \(\Delta t_A=\frac{L}{c-v}; \; \Delta t_B=\frac{L}{c+v}\);
— в системе К' \(\Delta t_A'=\Delta t_B' = \gamma \frac{L}{c}\) .
Заметьте. Символами \( t\) у меня обозначаются моменты времени. Промежутки времени обозначаются символами \(\Delta t\) .
Вы можете определить времена старта и финиша процесса
Какого процесса? У нас два процесса — полёт фотона направо и полёт фотона налево. Момент старта этого процесса \(t_0=t_0'=0\) .
Любого процесса.
Например, процесса первого путешествия Колумба в Америку?
Давайте всё-таки серьёзнее.

#64037 zam :#63995 Fedor :Однако приведенные масштабы соответствуют неподвижной конструкции интерферометра.
Какие ещё масштабы??
Вы это тоже понимаете.
Не понимаю. Приведите ссылку/цитату на учебник, где рассказывается про масштабы в СТО.
Нет таких учебников, в которых рассматривается данная задача. Я говорю не о масштабах СТО, а о размерах приведенной на рисунке конструкции.
Свет распространяется со скоростью «с» относительно чего угодно (второй постулат СТО)..
Вы забываете, что являетесь наблюдателем лабораторной системы отсчета,
Я вообще не являюсь наблюдателем. Я решаю задачу, а в процессе решения ставлю смебя на место наблюдателя то в системе К (смотрю из лаборатории на пролетающий мимо меня стержень), то в системе К' (сижу на стержне).
Похоже, что так.
Теперь я буду наблюдателем из лабораторной системы отсчета. Имеем две инерциальные системы отсчета: K – неподвижную лабораторную и K’ — движущуюся со скоростью v, в которой находятся стержни с источником. Условия задачи будем считать известными.
Используемые величины и их обозначения
Lи L’ =ГL –длины стержней в лабораторной и движущейся СО;
X’A=L’, X’B=-L’ – координаты концов стержней, в которых находятся регистраторы времени;
XA= L, XB=-L – координаты концов стержней в лабораторной СО в момент старта;
X'0 =0, X0=0 – координаты источника в момент старта;
t'0 =t0 =0 - момент пуска фотонов в месте расположения источника излучения;
t’A=t’B=0 – моменты включения регистраторов в точках их расположения.
tA, tB – времена старта процесса в пунктах XA и XB лабораторной СО;
tAF, tBF –времена финиша фотонов в СО К;
t’AF , t’BF – времена выключения регистраторов в СО K';
tAL, tBL – длительности полетов фотонов в СО К в период между их стартом и финишем на регистраторах.
Для преобразования времени используем формулу t' =Г(t-xv/c2).
Моменту времени t'=0 соответствуют моменты tA=xv/c2=Lv/c2, tB=xv/c2=-Lv/c2.
В лабораторной СО свет относительно регистраторов движется со скоростями c-v и c+v. При этом каждый из фотонов должен пройти путь, равный длине стержня в системе K, который в лабораторной системе равен L. Поэтому в лабораторной системе отсчета длительность пути света от момента старта до момента встречи с регистратором A равна tAL=L/(c-v). При этом время финиша фотона A в точке XA лабораторной СО суммируется с временем, которое было в этой точке в момент старта процесса tAF=tA+tAL= L/(c-v)+ Lv/c2. Соответственно время финиша фотона в пункте В определится выражением tBF=tB+tBL= L/(c+v)- Lv/c2. Полученные величины можем подставить в формулу преобразования для t’ и получить времена финиша, зарегистрированные регистраторами в СО K’.
t’AF=Г(tAF –Lv/c2)= Г(L/(c-v)+Lv/c2-Lv/c2)=ГL/(c-v)
t’BF=Г(tBF +Lv/c2)= ГL/(c+v)
Теперь можете возражать.

#64069 Fedor :#64037 zam :Не понимаю. Приведите ссылку/цитату на учебник, где рассказывается про масштабы в СТО.
Нет таких учебников, в которых рассматривается данная задача.
Сколько угодно.
Я говорю не о масштабах СТО, а о размерах приведенной на рисунке конструкции.
Размеры определены буковкой L. Какое хотите число, такое и подставьте.
Похоже, что так.
Теперь я буду наблюдателем из лабораторной системы отсчета. Имеем две инерциальные системы отсчета: K – неподвижную лабораторную и K’ — движущуюся со скоростью v, в которой находятся стержни с источником. Условия задачи будем считать известными.
Используемые величины и их обозначения
Lи L’ =ГL –длины стержней в лабораторной и движущейся СО;
X’A=L’, X’B=-L’ – координаты концов стержней, в которых находятся регистраторы времени;
XA= L, XB=-L – координаты концов стержней в лабораторной СО в момент старта;
X'0 =0, X0=0 – координаты источника в момент старта;
t'0 =t0 =0 - момент пуска фотонов в месте расположения источника излучения;
Тут всё верно.
t’A=t’B=0 – моменты включения регистраторов в точках их расположения.
Регистраторы — это не секундомеры. Они не включаются и не выключаются. В моменты t=0 и t'=0 с ними ничего не происходит.
tA, tB – времена старта процесса в пунктах XA и XB лабораторной СО;
В пунктах XA и XB ничего не стартует.
tAF, tBF –времена финиша фотонов в СО К;
У меня это обзначено tA и tB.
t’AF , t’BF – времена выключения регистраторов в СО K';
Регистраторы не выключаются. Времена финиша фотонов в СО К' у меня обозначены tA' и tB'.
tAL, tBL – длительности полетов фотонов в СО К в период между их стартом и финишем на регистраторах.
У меня это обзначено \(\Delta t_A\) и \(\Delta t_B\) .
Для преобразования времени используем формулу t' =Г(t-xv/c2).
Моменту времени t'=0 соответствуют моменты tA=xv/c2=Lv/c2, tB=xv/c2=-Lv/c2.
В момент t'=0 в точках x=L и x=-L никаких событий не происходит.
В лабораторной СО свет относительно регистраторов движется со скоростями c-v и c+v.
В лабораторной СО что угодно может двигаться только относительно СО. Нельзя в лабораторной СО двигаться относительно регистратора. Относительно регистратора можно двигаться только в СО регистратора (то есть, в СО стержней).
c-v и с+v — это скорости сближения света с регистраторами в лабораторной СО.
При этом каждый из фотонов должен пройти путь, равный длине стержня в системе K, который в лабораторной системе равен L.
Нет. В системе К фотоны проходят расстояния \(\Delta x_A=c\Delta t_A=L\frac{c}{c-v}\) и \(\Delta x_B=c\Delta t_B=L\frac{c}{c+v}\) .
Поэтому в лабораторной системе отсчета длительность пути света от момента старта до момента встречи с регистратором A равна tAL=L/(c-v).
Правильно. Продолжительность движения фотона равна \(\Delta t_A=\frac{L}{c-v}\) .
При этом время финиша фотона A в точке XA лабораторной СО суммируется с временем, которое было в этой точке в момент старта процесса tAF=tA+tAL= L/(c-v)+ Lv/c2.
Какое ещё суммирование??? Фотон стартовал в момент t=0. Время в пути \(\Delta t_A=\frac{L}{c-v}\) . Значит, момент финиша \( t_A=\frac{L}{c-v}\) .
Соответственно время финиша фотона в пункте В определится выражением tBF=tB+tBL= L/(c+v)- Lv/c2.
Соответственно \( t_B=\frac{L}{c+v}\) .
Полученные величины можем подставить в формулу преобразования для t’ и получить времена финиша, зарегистрированные регистраторами в СО K’.
t’AF=Г(tAF –Lv/c2)= Г(L/(c-v)+Lv/c2-Lv/c2)=ГL/(c-v)
t’BF=Г(tBF +Lv/c2)= ГL/(c+v)
Конечно. Только нужно подставлять правильно найденные величины.
\(t_A'=\gamma \left ( t_A-\frac{vx_A}{c^2} \right )=\gamma \left ( \frac{L}{c-v}-\frac{vL\frac{c}{c-v}}{c^2} \right )=\gamma \frac{L}{c}\)
\(t_B'=\gamma \left ( t_B-\frac{vx_B}{c^2} \right )=\gamma \left ( \frac{L}{c+v}-\frac{-vL\frac{c}{c+v}}{c^2} \right )=\gamma \frac{L}{c}\)
Теперь можете возражать.
А вам самому не показалось странным, что в системе К' фотоны приходят к резистраторам в разные моменты времени? В этой СО стержни покоятся. Источник света покоится. Регистраторы покоятся. Длины стержней одинаковы. Чем же направление «направо» отличается от направления «налево»?

#64098 zam :#64069 Fedor :При этом время финиша фотона A в точке XA лабораторной СО суммируется с временем, которое было в этой точке в момент старта процесса tAF=tA+tAL= L/(c-v)+ Lv/c2.
Какое ещё суммирование??? Фотон стартовал в момент t=0. Время в пути \(\Delta t_A=\frac{L}{c-v}\) . Значит, момент финиша \( t_A=\frac{L}{c-v}\) .
Соответственно время финиша фотона в пункте В определится выражением tBF=tB+tBL= L/(c+v)- Lv/c2.
Соответственно \( t_B=\frac{L}{c+v}\) .
Полученные величины можем подставить в формулу преобразования для t’ и получить времена финиша, зарегистрированные регистраторами в СО K’.
t’AF=Г(tAF –Lv/c2)= Г(L/(c-v)+Lv/c2-Lv/c2)=ГL/(c-v)
t’BF=Г(tBF +Lv/c2)= ГL/(c+v)
Конечно. Только нужно подставлять правильно найденные величины.
\(t_A'=\gamma \left ( t_A-\frac{vx_A}{c^2} \right )=\gamma \left ( \frac{L}{c-v}-\frac{vL\frac{c}{c-v}}{c^2} \right )=\gamma \frac{L}{c}\)
\(t_B'=\gamma \left ( t_B-\frac{vx_B}{c^2} \right )=\gamma \left ( \frac{L}{c+v}-\frac{-vL\frac{c}{c+v}}{c^2} \right )=\gamma \frac{L}{c}\)
Теперь можете возражать.
Итак, мы столкнулись с непониманием того, как работает формула преобразования времени
t' =Г(t-xv/c 2 ). Давайте разберемся с этим. Пусть есть две инерциальных системы отсчета К – неподвижная и K’ –движущаяся со скоростью v. Пусть в системе K’ происходит процесс, начало которого характеризуется координатами x0=x’0 =0, t0=t’0 =0. Пусть финиш процесса происходит в точке x’A=L’ в момент времени t’F. Нужно определить время финиша процесса в СО К, которое соответствует произвольной координате x в системе К.
Следует помнить, что часы (время) в любой системе отсчета идут в одинаковом темпе независимо от пространственной координаты. С целью удобства в системе K’ выставляем все часы на одно показание. Таким образом, старт процесса происходит в момент t’ =0 во всех пунктах пространственной координаты.
Однако при таком предположении в системе К старт процесса происходит при разных показаниях часов, которые определяются формулой преобразования и зависят от координаты места расположения. В результате время старта процесса ( t’=0) в системе К будет равно tS=xv/c2, в какой бы точке x часы не находились. Заметим, что их ход имеет одинаковый темп.
Пусть длительность процесса в пересчете на систему К равна DT. В момент финиша процесса все часы ОС К покажут время tF= tS+DT. Вот это время tF имеет отношение к формуле преобразования и его следует подставлять в формулу, чтобы узнать время финиша процесса в ОС K’.
А вам самому не показалось странным, что в системе К' фотоны приходят к резистраторам в разные моменты времени? В этой СО стержни покоятся. Источник света покоится. Регистраторы покоятся. Длины стержней одинаковы. Чем же направление «направо» отличается от направления «налево»?
Отличается оно тем, что принцип постоянства скорости света во всех ИСО не работает. Свет распространяется независимо от движения системы отсчета. В нашей задаче его скорость постоянна только в лабораторной СО. В случае с экспериментом Саньяка величину скорости света определяла воздушная атмосфера своим показателем преломления. То же самое она делала и в экспериментах Майкельсона.
отредактировал(а) Fedor: 2024-06-21 23:43 GMT

Подведем итоги того, что мы получили в результате мысленного эксперимента. Используя две инерциальные системы отсчета в мысленном эксперименте, который моделировал условия эксперимента Саньяка, мы получили такой же, как и полученный Саньяком результат. При рассмотрении эксперимента с точки зрения лабораторной системы отсчета разность во времени прихода к месту регистрации одновременно излученных световых сигналов определяется разностью в длинах путей сигналов, движущихся в противоположных направлениях. Такой результат следует как при рассмотрении процесса с точки зрения классической механики, так и при использовании преобразований специальной теории относительности. Результаты расчетов по длительности времени движения сигналов от старта до финиша различаются лишь присутствием лорец-фактора в качестве множителя в расчетах с использованием СТО. Полученный в лабораторной СО с использованием преобразований СТО результат вступает в противоречие с результатом рассмотрения того же процесса с точки зрения системы отсчета, в которой покоится источник излучения. Согласно второму постулату СТО скорость света в этой системе отсчета тоже равна c, поэтому оба световые сигналы должны прибыть к финишу одновременно. Однако они прибывают не одновременно вследствие очевидного неравенства путей каждого из сигналов в лабораторной СО. Неравенство длины пути одного сигнала в одном процессе с точки зрения разных систем отсчета также является очевидным. В системе отсчета источника длина пути светового сигнала равна длине стержня, а в лабораторной СО длина его же пути оказывается больше или меньше длины стержня в зависимости от направления распространения. Разные длины пути при одинаковой скорости света дают разную продолжительность времени на движение сигнала с места старта к месту финиша. Но один и тот же сигнал не может прибыть к финишу в разное время. Время прибытия у него одно так же, как и время старта. Одновременность расчетного прибытия сигнала к финишу при разных длинах его пути может быть обеспечена лишь разной скоростью света в разных системах отсчета. Таким образом, мы приходим к выводу о том, что гипотеза о постоянстве скорости света в инерциальных системах отсчета оказывается несостоятельной.

#64116 Fedor :Итак, мы столкнулись с непониманием того, как работает формула преобразования времени
«Простите, не мы, а вы”. ©
t' =Г(t-xv/c 2 ).
\(t'=\gamma \left ( t-\frac{vx}{c^2} \right )\; \; \; \; (1) \\x'=\gamma \left ( x-vt \right )\; \; \; \; (2) \\t=\gamma \left ( t'+\frac{vx'}{c^2} \right )\; \; \; \; (3) \\x=\gamma \left ( x'+vt' \right )\; \; \; \; (4)\)
Давайте разберемся с этим. Пусть есть две инерциальных системы отсчета К – неподвижная и K’ –движущаяся со скоростью v. Пусть в системе K’ происходит процесс, начало которого характеризуется координатами x0=x’0 =0, t0=t’0 =0.
То есть, имеем событие «О», старт процесса. Его координаты в системе К’: \(\left ( t_O'=0,x_O'=0 \right )\).
А в системе К координаты этого события \( \left ( t_O=0,x_O=0 \right )\). Это условие применимости простейшего вида преобразований Лоренца (1-4).
Пусть финиш процесса происходит в точке x’A=L’ в момент времени t’F.
Имеем событие “F”, финиш процесса, с координатами \(\left ( t_F',x_F'=L' \right )\). Я заменил обозначение x’A на x’F. Зачем лишние буквы?
Нужно определить время финиша процесса в СО К, которое соответствует произвольной координате x в системе К.
Координаты события «F» определяются преобразованиями Лоренца:\( \left ( t_F=\gamma \left ( t'_F+\frac{vL'}{c^2} \right ),x_F=\gamma \left ( L'+vt'_F \right ) \right )\) .
И никакой «произвольной координаты x». Событие «F» происходит в конкретном месте. Координаты события в системе К’ связаны взаимно однозначно с координатами того же самого события в системе К.
Следует помнить, что часы (время) в любой системе отсчета идут в одинаковом темпе независимо от пространственной координаты.
Время не идёт. Темп хода часов не зависит ни от пространственных, ни от временных координат. Зато зависит от скорости часов относительно системы отсчёта.
С целью удобства в системе K’ выставляем все часы на одно показание.
Это называется так – собственные (то есть покоящиеся) часы системы К’ синхронизированы.
Таким образом, старт процесса происходит в момент t’ =0 во всех пунктах пространственной координаты.
Старт процесса в системе К’ происходит в единственном пункте x’O = 0. В системе К’ все её собственные часы в этот момент показывают ноль.
Рассмотрим одни из таких часов и определим событие «U» — стрелка данных часов показывает на деление «ноль». Координаты события «U»: \( (t_U'=0, x_U')\).
Однако при таком предположении в системе К старт процесса происходит при разных показаниях часов, которые определяются формулой преобразования и зависят от координаты места расположения.
Конечно. Часы, синхронизированные в одной ИСО, не являются синхронизированными в другой ИСО.
Старт процесса в системе К происходит в единственном пункте xО = 0. Собственные часы системы К’ в системе К показывают разное время.
В результате время старта процесса ( t’=0) в системе К будет равно tS=xv/c2, в какой бы точке x часы не находились. Заметим, что их ход имеет одинаковый темп.
Координаты события U в системе К следующие: \(\left ( t_U=\gamma \frac{vx_A'}{c^2}, x_U=\gamma x_A'\right ) \). Обратите внимание – в зависимости от величины xU’ величина tU может быть и меньше нуля, и больше нуля.
Пусть длительность процесса в пересчете на систему К равна DT.
\(\Delta T=t_F-t_O==\gamma \left ( t'_F+\frac{vL'}{c^2} \right )\) .
В момент финиша процесса все часы ОС К покажут время tF= tS+DT.
Все собственные часы системы К (то есть, покоящиеся в системе К) покажут это время.
Вот это время tF имеет отношение к формуле преобразования и его следует подставлять в формулу, чтобы узнать время финиша процесса в ОС K’.
Момент финиша процесса в системе К' вы определили в самом начале, Это \(t_F'\) . И оно совсем не равно \(\Delta T=\gamma \left ( t'_F+\frac{vL'}{c^2} \right )\) .
А вам самому не показалось странным, что в системе К' фотоны приходят к резистраторам в разные моменты времени? В этой СО стержни покоятся. Источник света покоится. Регистраторы покоятся. Длины стержней одинаковы. Чем же направление «направо» отличается от направления «налево»?
Отличается оно тем, что принцип постоянства скорости света во всех ИСО не работает.
А он работает, назло отцу Fedor'у. Никакие молитвы не помогают.
Свет распространяется независимо от движения системы отсчета.
В нашей задаче его скорость постоянна только в лабораторной СО.
Второе предложение противоречит первому.
В случае с экспериментом Саньяка
Рано вам про Саньяка. Вы ещё таблицу сложения в пределах десяти не освоили.

#64268 zam :#64116 Fedor :Итак, мы столкнулись с непониманием того, как работает формула преобразования времени
«Простите, не мы, а вы”. ©
t' =Г(t-xv/c 2 ).
\(t'=\gamma \left ( t-\frac{vx}{c^2} \right )\; \; \; \; (1) \\x'=\gamma \left ( x-vt \right )\; \; \; \; (2) \\t=\gamma \left ( t'+\frac{vx'}{c^2} \right )\; \; \; \; (3) \\x=\gamma \left ( x'+vt' \right )\; \; \; \; (4)\)
В формулах (3) и (4) Вы заменили функции систем отсчета. Теперь K’ стала неподвижной системой, а К – движущейся. С той лишь разницей, что теперь скорость пустой системы имеет другой знак. Таким образом, Вы изменили условия задачи и снова источник света посадили в неподвижную систему.
В момент финиша процесса все часы ОС К покажут время tF= tS+DT.
Все собственные часы системы К (то есть, покоящиеся в системе К) покажут это время.
Вы где учились шулерству? С такими фокусами можете выступать в цирке, но на форуме. У Вас все часы неподвижной системы K’ синхронизированы и показывают одно время, а для системы К будьте добры использовать вашу формулу (3).
Я не предлагаю Вам осваивать таблицу сложения. Вы ее знаете. Не способны Вы опровергнуть моих доводов о несостоятельности СТО даже путем мошенничества.

#64277 Fedor :#64268 zam :\(t'=\gamma \left ( t-\frac{vx}{c^2} \right )\; \; \; \; (1) \\x'=\gamma \left ( x-vt \right )\; \; \; \; (2) \\t=\gamma \left ( t'+\frac{vx'}{c^2} \right )\; \; \; \; (3) \\x=\gamma \left ( x'+vt' \right )\; \; \; \; (4)\)
В формулах (3) и (4) Вы заменили функции систем отсчета. Теперь K’ стала неподвижной системой, а К – движущейся.
Не выдумывайте. Формулы (3) и (4) — это элементарное следствие из формул (1) и (2) (попробуйте сами из системы (1)-(2) выразить переменные t и x, что получится?). Первая пара позволяет переводить результаты измерений из системы К в систему К', вторая пара — изи системы К' в систему К. Систему К по-прежнему считаем неподвижной.
С той лишь разницей, что теперь скорость пустой системы имеет другой знак. Таким образом, Вы изменили условия задачи и снова источник света посадили в неподвижную систему.
Враньё. Постарайтесь сначала думать и только потом писать сообщения.
В момент финиша процесса все часы ОС К покажут время tF= tS+DT.
Все собственные часы системы К (то есть, покоящиеся в системе К) покажут это время.
Вы где учились шулерству?
Вас что, забанить и в вольерах для павианов? Мало вам того, что вам запрещено публиковаться в тематических разделах? Лавры Александр. и Желяпокоя не дают?
Будете нарушать правила форума — буду ваши сообщения удалять.







