Перекатывание цилиндра в цилиндре

В нижней точке полого цилиндра находится другой цилиндр массой m, который начинает движение со скоростью vs0. Надо определить максимальный угол отклонения внутреннего цилиндра Ф.

В принципе задачу я решил. Просто выяснилось, что масса m никак не влияет на ответ. Или я не прав?

#61934 Seva :В нижней точке полого цилиндра находится другой цилиндр массой m, который начинает движение со скоростью vs0. Надо определить максимальный угол отклонения внутреннего цилиндра Ф.

В принципе задачу я решил.
У меня получилось 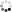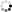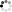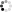 . А у вас?
. А у вас?
Просто выяснилось, что масса m никак не влияет на ответ. Или я не прав?
Вы правы. Также, как и максимальная высота подбрасываемого камня не зависит от массы камня, а зависит только от его начальной скорости.

То же самое. Поэтому и возник вопрос, зачем в задании дали массу.

Как я решал.



Если в ваш и мой варианты подставить любые численные значения (например, R = 0,5, r = 0,25, vs0 = 1, g = 9,81), то получатся одинаковые ответы, 37,240. Но самое интересное, что университетская система пишет, что ответ неверен. И предлагает варианты: Φ= 64, 230, Φ= 51, 850, Φ= 38, 120, Φ= 46, 040.

В принципе, у нас одинаковые решения.


#62899 Seva :Если в ваш и мой варианты подставить любые численные значения (например, R = 0,5, r = 0,25, vs0 = 1, g = 9,81), то получатся одинаковые ответы, 37,240.
Естественно. Потому что 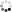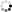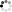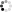 .
.
Но самое интересное, что университетская система пишет, что ответ неверен. И предлагает варианты: Φ= 64, 230, Φ= 51, 850, Φ= 38, 120, Φ= 46, 040.
А это потому, что мы оба ошиблись. Причём одинаково.
Закон сохранения энергии (изменение кинетической энергии) = (изменение потенциальной энергии):
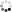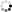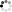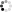 .
.
Здесь 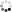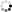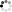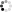 — момент инерции цилиндра,
— момент инерции цилиндра,
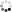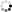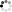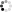 — начальная угловая скорость цилиндра.
— начальная угловая скорость цилиндра.
Отсюда
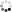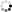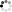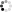
Четвёртый ответ.

Вот это да! Спасибо!





