Физика гравитации
А может следует уточнить, что пространство — это свойство материи. Да, формы материи могут искривляться, извиваться, изголяться, но всё это фиксируется в прямолинейном пространстве. Если бы пространство искривлялось, то как бы вы определили тип поверхности: прямая она или изогнута?
Личное сообщение
#61501 Fedor :#61499 zam :Не здоровье. Но вы путаете причину и следствие. Так как phi = arccos (a,b)/|a||b|, отсюда следует, что (a,b)=|a||b|cos(phi) .
Это Вы путаете причину и следствие. Понятие об угле появилось у людей значительно раньше скалярного произведения.
Понятие об угле между векторами появилось ровно тогда, когда появилось понятие векторов (конец 19 века).
Хорошо. Вот вам пара векторов: \(\vec{a}=\begin{pmatrix}5\\ 7\\ -3\\ 9 \end{pmatrix}\) и \(\vec{b}=\begin{pmatrix}4\\ 0\\ -8\\ 0\end{pmatrix}\) . Определите угол между ними.
Если метрический тензор содержит положительные единицы по диагонали, а все остальные компоненты нули, то пространство эвклидово (плоское).
Если метрический тензор содержит положительные и отрицательные единицы по диагонали, а все остальные компоненты нули, то это пространство Минковского (тоже плоское).
Если есть отличные от нуля недиагональные элементы, то пространство искривлённое.
Не следует повторять то, что я писал Вам ранее в этой же теме.
Почему же не следует? Вы списали не понимая, что списываете. А я вам объясняю, что у вас написано.
#61505 Желя :А может следует уточнить, что пространство — это свойство материи.
Пространство — это не свойство материи. Пространство не материально.
фиксируется в прямолинейном пространстве.
Нет никакого прямолинейного пространства. Пространства бывают Эвклида, Лобачевского, Римана, Минковского, Гильберта, плоские, искривлнные, топологические, проективные, вероятностные и многие какие ещё. А вот прямолинейного — не бывает.
Если бы пространство искривлялось, то как бы вы определили тип поверхности: прямая она или изогнута?
Кривизну пространства определить достаточно просто. Нужно построить треугольник и измерить его углы. Если сумма углов равна \(\pi \) , то пространство плоское. Иначе — искривлённое.
Замечу: кривизна пространства не имеет никакого отношения к кривизне поверхности, в это пространство вложенной.
#61531 zam :Понятие об угле между векторами появилось ровно тогда, когда появилось понятие векторов (конец 19 века).
Печально, что Ньютон не имел понятия о векторах.
Хорошо. Вот вам пара векторов: \(\vec{a}=\begin{pmatrix}5\\ 7\\ -3\\ 9 \end{pmatrix}\) и \(\vec{b}=\begin{pmatrix}4\\ 0\\ -8\\ 0\end{pmatrix}\) . Определите угол между ними.
Значения координат векторов Вы дали, а где метрический тензор? В какой системе координат? x,y,z,t? В такой записи я могу вычислить только их скалярное произведение. (a,b) = axbx+ayby+azbz+atbt. Числа можете самостоятельно подставить.
Не следует повторять то, что я писал Вам ранее в этой же теме.
Почему же не следует? Вы списали не понимая, что списываете. А я вам объясняю, что у вас написано.
Чтобы Вам дойти до моего понимания, нужно было бы прослушать двухлетний курс аналитической геометрии и векторного анализа. Сдать без хвостов все зачеты и экзамены Гестрину Геннадию Николаевичу, который на первом экзамине по этому предмету 60 студентов моего курса отправил с хвостами. Между прочим курс состоял не из дураков — 37 выпускников стали кандидатами наук и 7 докторами.
отредактировал(а) Fedor: 2024-04-10 14:01 GMT
#61536 Fedor :#61531 zam :Понятие об угле между векторами появилось ровно тогда, когда появилось понятие векторов (конец 19 века).
Печально, что Ньютон не имел понятия о векторах.
Зато он изобрёл дифференциальное и интегральное исчисление. Это покруче будет.
Хорошо. Вот вам пара векторов: \(\vec{a}=\begin{pmatrix}5\\ 7\\ -3\\ 9 \end{pmatrix}\) и \(\vec{b}=\begin{pmatrix}4\\ 0\\ -8\\ 0\end{pmatrix}\) . Определите угол между ними.
Значения координат векторов Вы дали, а где метрический тензор?
Вооот!!! Без метрического тензора эту задачу не решить.
В какой системе координат? x,y,z,t?
В какой угодно. Например (температура в Ашхабаде, курс дорллара на Московской бирже, показание электросчётчика в вашей квартире, количество пингвинов в Антарктиде).
В такой записи я могу вычислить только их скалярное произведение. (a,b) = axbx+ayby+azbz+atbt.
Не можете. У вас же нет метрического тензора!!
Не следует повторять то, что я писал Вам ранее в этой же теме.
Почему же не следует? Вы списали не понимая, что списываете. А я вам объясняю, что у вас написано.
Чтобы Вам дойти до моего понимания, нужно было бы прослушать двухлетний курс аналитической геометрии и векторного анализа. Сдать без хвостов все зачеты и экзамены Гестрину Геннадию Николаевичу, который на первом экзамине по этому предмету 60 студентов моего курса отправил с хвостами. Между прочим курс состоял не из дураков — 37 выпускников стали кандидатами наук и 7 докторами.
А я-то, наивный, считал, что вы только семинарию закончили.
И после этого вы утверждаете, что равномерное движение по окружности есть движение без ускорения?
Может, вы на самом деле заболели душевно? Что-то я волноваться за вас стал.
отредактировал(а) zam: 2024-04-10 15:49 GMT
#61532 zam :Пространство — это не свойство материи. Пространство не материально.
Нет никакого прямолинейного пространства. Пространства бывают Эвклида, Лобачевского, Римана, Минковского, Гильберта, плоские, искривлнные, топологические, проективные, вероятностные и многие какие ещё. А вот прямолинейного — не бывает.
Кривизну пространства определить достаточно просто. Нужно построить треугольник и измерить его углы. Если сумма углов равна \(\pi \) , то пространство плоское. Иначе — искривлённое.
Замечу: кривизна пространства не имеет никакого отношения к кривизне поверхности, в это пространство вложенной.
Я веду речь о пространстве материи, которая всё. Вы о пространстве нематерии, которе ничто. Согласен, что между всем и ничем есть разница. Вы её чувствуете?
Пространство бывает разное: твёрдое, жидкое, газообразное. Оно и такое, и сякое, и кто его знанет какое. Вам откуда знать, как его величать?
Прямую плоскость определяют три прямые, соединённые в треугольник, да и то, если недалёко, а криволинейный треугольник может иметь любую сумму углов. Потренируйтесь на досуге.
Кстати, вы всегда такой заметчивый? Это особенно видно по СТО.
#61541 Желя :Я веду речь о пространстве материи, которая всё.
Нет никакого пространства материи. Вы пустомелите о том, чего нет.
Вы о пространстве нематерии, которе ничто.
А я рассказываю просто о пространстве — чётко определённом научном термине. Почитайте в Математической энциклопедии, что это такое.
Пространство бывает разное: твёрдое, жидкое, газообразное.
Твёрдым, жидким, газообразным бывает состояние вещества. Какими бывают пространства я вам перечислил ранее (и это далеко не полный список).
Прямую плоскость определяют три прямые, соединённые в треугольник, да и то, если недалёко,
Что значит «недалеко»? А известен вам термин «косая плоскость»?
а криволинейный треугольник может иметь любую сумму углов. Потренируйтесь на досуге.
А речь не про криволинейный треугольник. Речь про треугольник из прямых отрезков (отрезков геодезических).
Кстати, вы всегда такой заметчивый? Это особенно видно по СТО.
Ну, выдающиеся глупости обычно замечаю. А что вы можете видеть по СТО, когда вы СТО не знаете? Ровно ноль.
#61545 zam :Нет никакого пространства материи. Вы пустомелите о том, чего нет
Когда отрицается пространство материи: лесов, полей и рек, невольно задаёшь сам себе вопрос: не пустомеля ли отрицает это? А может слепой, что очевидного не видит?
#61545 zam :А я рассказываю просто о пространстве — чётко определённом научном термине. Почитайте в Математической энциклопедии, что это такое
Вы пространство лесов, полей и рек видали? Вот с учётом этих пространств и определим научный термин. Я почитал энциклопедию и понял, что пространство бывает разное...
#61545 zam :Твёрдым, жидким, газообразным бывает состояние вещества. Какими бывают пространства я вам перечислил ранее (и это далеко не полный список).
Вещество — это одно из состояний материи.Я просто дополнил список метериальных пространств. Что вас не устраивает?
#61545 zam :Что значит «недалеко»? А известен вам термин «косая плоскость»?
Известен. Термин «косой» говорит о повреждении зрения наблюдателя. Лечитесь. Заодно повышайте обрзовательный уровень. Прямая плоскость, по мнению некоторых, может быть представлена и двумя пересекающимися прямыми. А о термине «недалёко» поговорим особо, когда ваш бзык пройдёт.
#61545 zam :А речь не про криволинейный треугольник. Речь про треугольник из прямых отрезков (отрезков геодезических)
А кто вам сказал, что геодезические отрезки прямолинейны?
#61537 zam :#61536 Fedor :И после этого вы утверждаете, что равномерное движение по окружности есть движение без ускорения?
Может, вы на самом деле заболели душевно? Что-то я волноваться за вас стал.
Можете не волноваться. Лучше сами подумайте. Да, изменение направления движения тела выполняет центростремительная сила, направленная в сторону центра кривизны. Она принуждает тело менять направление его движения. В отсутствие сопротивления со стороны тела оно двигалось бы к центру кривизны с ускорением. Однако в результате инерции тело продолжает лететь по касательной в каждой точке круговой траектории, отрываясь от нее тоже с ускорением. В результате два ускорения компенсируют друг друга в случае движения по кругу. При этом модули обоих ускорений равны v2/R. В результате суммарное ускорение обращается в нуль и тело остается на круговой траектории.
#61545 zam :Ну, выдающиеся глупости обычно замечаю. А что вы можете видеть по СТО, когда вы СТО не знаете? Ровно ноль.
Я тоже считаю, что если глупость не знают и знать не желают, то это самая большая глупость из всех глупостей. Тут речь не о гравитации, в которой только одна из масс не притягивается, тут о глупости высокого масштаба речь идёт. Да, Мне достаточно знать, что в СТО правды ровно ноль, и что лоренц-фактор это ложь, который можно вывести только по принципу 2х2 = 4 = 5 = 7. Можете дальше твердить, что в СТО я ноль. Мне почти всё равно. Интересно, что ваши внуки запоют, когда с опозданием узнают, что 2х2 = 4, а не 5 и не 7, как в СТО?
#61537 zam :И после этого вы утверждаете, что равномерное движение по окружности есть движение без ускорения?
Действительно, признавая существование центростремительного ускорения, я утверждаю, что движение по окружности происходит при суммарном нулевом ускорении и вот почему.
Итак, центростремительное ускорение при круговом движении создается центральной силой, имеющей направление к центру кривизны. Это я признаю.
Теперь рассмотрим движение по круговой траектории, расположенной на плоскости XY с центром, совпадающим с началом системы координат. Будем считать, что положительное направление оси X совпадает с положением угла ф=0. В таком случае компоненты скорости движущегося по окружности тела можно записать в виде:
v x= vsinф, vy=vcosф
Производные по времени (ускорения) от этих компонент запишем в виде
a x= vcosф dф/dt, ay=-vsinф dф/dt
Заметим, что dф/dt=v/R. Нетрудно видеть, что в точке ф=0 ax=v2/R. В этой точке направление оси X совпадает с направлением радиуса кривизны траектории. Таким образом, это ускорение направлено в противоположном направлении центростремительному ускорению и равно ему по модулю. Надеюсь, zam поймет, что результат сложения этих ускорений равен нулю.
deleted
Напоминаю. Данному субъекту публиковаться на форуме ЗАПРЕЩЕНО!
Все ссобщения будут удаляться без предупреждения.
отредактировал(а) zam: 2024-04-11 14:39 GMT
#61572 Виктор Михайлович :Ф, Ф,
Какие два ускорения?!?!
Не надо жонглировать математикой, надо думать о физике.
Физика и математика не противоречащие друг другу представлены в моих двух последних сообщениях. Найдите в них ошибку. Я понимаю, что Вы относитесь к категории людей, которые продолжают верить в то, что Ирод отправил Христа на распятье даже в том случае, когда узнают, что Ирод умер за четыре года до рождения Христа.
#61584 Виктор Михайлович :Я уже показал. что к одному телу приложены два действия — одно приложенное извне, и второе — инерционное противодействие изменению движения тела (3-ий закон), но одно тело имеет только одно движение, т.е. оно не может продолжать лететь по касательной испытывая при этом ценростремительное ускорение..
Ваша математика противоречит именно единственности движения.
Результаты математики нисколько не противоречат единственности движения, которое выражается в круговой траектории с постоянным радиусом кривизны. Нужно только понять, что заставляет двигаться тело именно по такой траектории. Следует помнить, что в каждой точке траектории скорость тела направлена вдоль касательной к траектории. В отсутствие центростремительной силы при смещении тела на минимальное расстояние dl вдоль касательной тело одновременно смещается в сторону увеличения радиуса — расстояния от центра кривизны. Это отклонение от круговой траектории происходит с ускорением, которое называют центробежным. Его величина равна v2/R. Но!!! В это же время центростремительная сила возвращает тело на постоянную траекторию с таким же ускорением. Единственность движения при этом никак не нарушается. Вы оказываетесь заколдованным только центростремительной силой и связанным с ней ускорением, забывая при этом, что тело имеет скорость, направленную по касательной, то есть в сторону отрыва от круговой траектории.
#61558 Fedor :#61537 zam :#61536 Fedor :И после этого вы утверждаете, что равномерное движение по окружности есть движение без ускорения?
Да, изменение направления движения тела выполняет центростремительная сила, направленная в сторону центра кривизны. Она принуждает тело менять направление его движения.
Верно. Только лучше «центростремительная сила». Термин «центральная сила» имеет несколько другое значение.
В отсутствие сопротивления со стороны тела оно двигалось бы к центру кривизны с ускорением.
Оно и двигается с ускорением, направленным к центру. Но направление движения (то есть скорости) не обязано совпадать с направлением ускорения.
И никакого «сопротивления со стороны тела», да ещё и приложенного к самому телу, в природе не существует.
Однако в результате инерции тело продолжает лететь по касательной в каждой точке круговой траектории, отрываясь от нее тоже с ускорением.
Тело не летит по касательной. Оно движется по окружности.
В результате два ускорения компенсируют друг друга в случае движения по кругу.
У тела может быть только одно ускорение. Оно либо равно нулю, либо нет. При движении по окружности оно не равно нулю и направлено к центру.
#61563 Fedor :#61537 zam :И после этого вы утверждаете, что равномерное движение по окружности есть движение без ускорения?
Действительно, признавая существование центростремительного ускорения, я утверждаю, что движение по окружности происходит при суммарном нулевом ускорении и вот почему.
Итак, центростремительное ускорение при круговом движении создается центральной силой, имеющей направление к центру кривизны. Это я признаю.
Теперь рассмотрим движение по круговой траектории, расположенной на плоскости XY с центром, совпадающим с началом системы координат. Будем считать, что положительное направление оси X совпадает с положением угла ф=0.
Вот! Это уже серьёзный разговор. Я не поленился, картинку нарисовал:
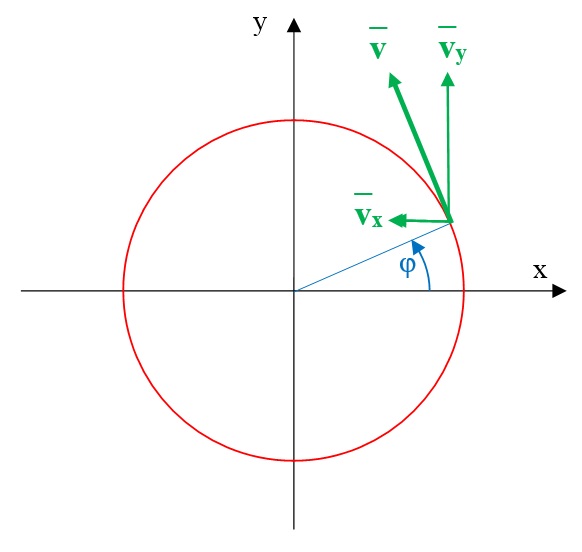
В таком случае компоненты скорости движущегося по окружности тела можно записать в виде:
v x= vsinф, vy=vcosф
Вы ошиблись. Проекции скорости на оси координат выглядят следующим образом:
\(\left\{\begin{matrix}v_x=-vsin\varphi \\ v_y=vcos\varphi \end{matrix}\right .\)
Перед \(vsin\varphi\) должен стояить «минус».
Производные по времени (ускорения) от этих компонент запишем в виде
a x= vcosф dф/dt, ay=-vsinф dф/dt
Верно.
\( \left\{\begin{matrix}a_x=\frac{dv_x}{dt}=-vcos\varphi \frac{d\varphi }{dt}\\ a_y=\frac{dv_y}{dt}=-vsin\varphi \frac{d\varphi }{dt}\end{matrix}\right. \)
Заметим, что dф/dt=v/R.
Верно. \(\frac{d\varphi }{dt}=\frac{v}{R}\). Поэтому
\(\left\{\begin{matrix}a_x=-\frac{v^2}{R}cos\varphi \\ a_y=-\frac{v^2}{R}sin\varphi\end{matrix}\right.\)
Нетрудно видеть, что в точке ф=0 ax=v2/R.
Нетрудно видеть, что в точке \(\varphi =0\) \(a_x=-\frac{v^2}{R}\) .
В этой точке направление оси X совпадает с направлением радиуса кривизны траектории. Таким образом, это ускорение направлено в противоположном направлении центростремительному ускорению и равно ему по модулю.
Таким образом, это ускорение направлено к центру. Поэтому называется центростремительным.
Надеюсь, zam поймет, что результат сложения этих ускорений равен нулю.
Надеюсь, вы будете более аккуратными с математическими преобразованиями.
#61588 zam :Надеюсь, вы будете более аккуратными с математическими преобразованиями.
С поправкой я согласен. Действительно, я не был внимателен в записи компонента скорости по координате X. Тем не менее, это не меняет моего мнения о сути движения по круговой траектории.
Двигаясь по круговой траектории, тело одновременно движется и в направлении касательной к траектории. В любой точке траектории тела эти направления совпадают. Следовательно, сместившись на угол dф вдоль направления касательной тело может переместиться на радиус dR, который вычислим с помощью теоремы Пифагора. После смещения тела на угол dф вдоль касательной можно записать равенство (R+dR)2=R2+(Rsindф)2. Ввиду малости dф положим sindф = dф. Далее не сложно получить оценку для прироста радиуса dR=R(dф)2/2.
Производная dR/dt=Rdфd(dф)/dt= Rdфv/R=vdф дает радиальную скорость перемещения тела. Вторая производная дает радиальное ускорение
a r=d2R/dt2=v2/R
Нетрудно видеть, что учет движения тела в направлении касательной приводит к такому же ускорению, только другого направления.
3-й закон Ньютона гласит: Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.
А вот гравитация тел требует объяснения. И самое главное: почему оно (объяснение) не находит места в классической физике?
#61586 zam :#61558 Fedor :#61537 zam :#61536 Fedor :И после этого вы утверждаете, что равномерное движение по окружности есть движение без ускорения?
Да, изменение направления движения тела выполняет центростремительная сила, направленная в сторону центра кривизны. Она принуждает тело менять направление его движения.
Верно. Только лучше «центростремительная сила». Термин «центральная сила» имеет несколько другое значение.
В отсутствие сопротивления со стороны тела оно двигалось бы к центру кривизны с ускорением.
Оно и двигается с ускорением, направленным к центру. Но направление движения (то есть скорости) не обязано совпадать с направлением ускорения.
И никакого «сопротивления со стороны тела», да ещё и приложенного к самому телу, в природе не существует.
Однако в результате инерции тело продолжает лететь по касательной в каждой точке круговой траектории, отрываясь от нее тоже с ускорением.
Тело не летит по касательной. Оно движется по окружности.
В результате два ускорения компенсируют друг друга в случае движения по кругу.
У тела может быть только одно ускорение. Оно либо равно нулю, либо нет. При движении по окружности оно не равно нулю и направлено к центру.
Уважаемый zam и Фёдор, что-то Вы запутали меня с этой Вашей формулой a = v^2 / R, объясните пожалуйста, каким образом и из каких условий получена Ваша формула a = v^2 / R и можно ли её применить к системе Луна – Земля? Возможно я её понимаю не так, как Вы. Как из неё можно определить ускорение Луны? При необходимости вот Вам данные: масса Земли mз = 597,26*10^22кг, масса Луны mл = 7,3477*10^22кг, среднее расстояние между их центрами R = 384,467*10^6м. Если ещё что-то нужно, найдёте в интернете.
#61642 Хуснулла Алсынбаев :Уважаемый zam и Фёдор, что-то Вы запутали меня с этой Вашей формулой a = v^2 / R, объясните пожалуйста, каким образом и из каких условий получена Ваша формула a = v^2 / R и можно ли её применить к системе Луна – Земля? Возможно я её понимаю не так, как Вы. Как из неё можно определить ускорение Луны? При необходимости вот Вам данные: масса Земли mз = 597,26*10^22кг, масса Луны mл = 7,3477*10^22кг, среднее расстояние между их центрами R = 384,467*10^6м. Если ещё что-то нужно, найдёте в интернете.
Уважаемый Хуснулла, Луна примерно в 80 раз легче Земли, поэтому можно считать, что она движется вокруг Земли по круговой траектории в условиях гравитационного взаимодействия между Землей и Луной. Теперь о том, что заставляет двигаться Луну по кругу с постоянным радиусом. В каждой точке траектории Луны направление ее скорости совпадает с направлением касательной линии к траектории. Таким образом Луна одновременно имеет два направления движения — по кругу и по касательной. Если в какой-то момент гравитация прекратится, то Луна полетит по касательной. При этом расстояние между Землей и Луной будет увеличиваться. Увеличение это будет происходить с ускорением. Но мы знаем, что Земля притягивает Луну тоже с ускорением. В условиях движения Луны по кругу эти ускорения оказываются равными друг другу и поэтому радиус траектории остается неизменным.
Чтобы понять происходящее, приведу более простой пример. Для тренировки бегунов используют тренажеры — беговые дорожки. Дорожка с какой-то скоростью движется навстречу бегуну. а он, стараясь удержаться, с такой же скоростью бежит навстречу дорожке. В результате он остается на месте относительно зала, где тренируется. Мало того. он может пустить дорожку с небольшим ускорением, чтобы тренировать свои способности ускоряться. Тоже самое происходит в условиях движении Луны. С одной стороны она падает на Землю с ускорением g, а с другой — с таким же ускорением убегает с круговой траектории, двигаясь по касательной. В этом движении выполняется равенство g =vл2/R . Почему это ускорение равно vл2/R написано во многих учебниках и текстах, которые есть в этой теме.
отредактировал(а) Fedor: 2024-04-13 15:13 GMT
#61643 Fedor :Уважаемый Хуснулла, Луна примерно в 80 раз легче Земли, поэтому можно считать, что она движется вокруг Земли по круговой траектории в условиях гравитационного взаимодействия между Землей и Луной. Теперь о том, что заставляет двигаться Луну по кругу с постоянным радиусом. В каждой точке траектории Луны направление ее скорости совпадает с направлением касательной линии к траектории. Таким образом Луна одновременно имеет два направления движения — по кругу и по касательной. Если в какой-то момент гравитация прекратится, то Луна полетит по касательной. При этом расстояние между Землей и Луной будет увеличиваться. Увеличение это будет происходить с ускорением. Но мы знаем, что Земля притягивает Луну тоже с ускорением. В условиях движения Луны по кругу эти ускорения оказываются равными друг другу и поэтому радиус траектории остается неизменным.
Уважаемый дядя Фёдор, меня Ваш ответ не устраивает. Это как «Земля притягивает Луну тоже с ускорением»? «Если в какой-то момент гравитация прекратится, то Луна полетит по касательной. При этом расстояние между Землей и Луной будет увеличиваться», это мне понятно. Это как «В условиях движения Луны по кругу эти ускорения оказываются равными друг другу и поэтому радиус траектории остается неизменным.»? Покажите каким образом ускорения Земли и Луны будут равными? Или Вы хотите сказать, что ускорения Луны по кругу и по вертикали к Земле будут равными?
Покажите расчётным способом ускорение Луны, как я это просил, а Вы не сделали. Что ли Вам было лень? Я больше верю расчётам и числам, чем словоблудию.
А вот ZAM, я уверен, рассчитает, покажет и расскажет более подробно, Аллаха ему в помощь. Он не ленивый, в отличие от других. Да будет так!
#61645 Хуснулла Алсынбаев :Уважаемый дядя Фёдор, меня Ваш ответ не устраивает. Это как «Земля притягивает Луну тоже с ускорением»? «Если в какой-то момент гравитация прекратится, то Луна полетит по касательной. При этом расстояние между Землей и Луной будет увеличиваться», это мне понятно. Это как «В условиях движения Луны по кругу эти ускорения оказываются равными друг другу и поэтому радиус траектории остается неизменным.»? Покажите каким образом ускорения Земли и Луны будут равными? Или Вы хотите сказать, что ускорения Луны по кругу и по вертикали к Земле будут равными?
Покажите расчётным способом ускорение Луны, как я это просил, а Вы не сделали. Что ли Вам было лень? Я больше верю расчётам и числам, чем словоблудию.
А вот ZAM, я уверен, рассчитает, покажет и расскажет более подробно, Аллаха ему в помощь. Он не ленивый, в отличие от других. Да будет так!
Уважаемый Хуснулла, в моем сообщении №61591 показано, как образуется такое ускорение и что оно направлено по радиусу, то есть, строго в противоположном направлении гравитационному ускорению. Ускорения Луны по кругу нет, оно отсутствует и скорость Луны по кругу остается постоянной. Есть только два взаимно компенсирующих друг друга ускорения: гравитационное центростремительное — g и центробежное v2/R . А на пояснение zam-a не уповайте. Он этого механизма не понимает. В его понимании существует только одно ускорение g, которое дает гравитационное поле и оно тоже равно v2/R только направлено в сторону Земли. Он это показал в файле 61588.
#61646 Fedor :#61645 Хуснулла Алсынбаев :А вот ZAM, я уверен, рассчитает, покажет и расскажет более подробно, Аллаха ему в помощь. Он не ленивый, в отличие от других. Да будет так!
Уважаемый Хуснулла, в моем сообщении №61591 показано, как образуется такое ускорение и что оно направлено по радиусу, то есть, строго в противоположном направлении гравитационному ускорению. Ускорения Луны по кругу нет, оно отсутствует и скорость Луны по кругу остается постоянной. Есть только два взаимно компенсирующих друг друга ускорения: гравитационное центростремительное — g и центробежное v2/R . А на пояснение zam-a не уповайте. Он этого механизма не понимает. В его понимании существует только одно ускорение g, которое дает гравитационное поле и оно тоже равно v2/R только направлено в сторону Земли. Он это показал в файле 61588.
Уважаемый мной дедушка Фёдор, я Вас очень и очень уважаю, пожалуйста, рассчитайте по Вашей формуле ускорение Луны в некоторой точке на орбите и покажите, от какой скорости и от какого радиуса она зависит, и куда она направлена? Я так понимаю, скорость и ускорение подразумевает движение в некотором направление. Я больше верю цифрам, а не словам. В Вашем пункте №61591, только Ваша формула, а расчётов нет. Если Вы этого не сделаете, я так и останусь на вечно, прости меня Господи, о Аллах, неразумным в физике. Вы этого хотите? Не хорошо это. Научите меня, сделайте сегодня хоть одно Богоугодное дело и Аллах Вас наградит большой и вечной печатью на груд. Нуууу, если хотите, если Вам будет угодно, я попрошу его, можно и на Ваш умный лоб.
Что-то zam пропал, а то всегда бывал на месте, видимо расчёты делает. Явно что-то умное хочет выдать.
Теперь я постараюсь объяснить свою точку зрения. Она основана не на формулах а, на эксперименте, объясняющем притяжение тел. Это изменённый опыт Кавендиша, в котором горизонтальная сила взаимодействия масс, действующая на крутильные весы после изменения её человеком, заменена на естественное изменение вертикальных сил притяжения и Архимеда. Этот эксперимент выявил отсутствие горизонтальных сил притяжения масс при явном наличии таких же вертиальных сил. Возник естественный вопрос: массы тел не могут притягиваться вертикально, не притягиваясь горизонтально и наоборот, если массы тел притягивются вертикально, то как существует механизм, который не притягивает массы горизонтально?
zam этот ксперимент не расматривает, безапелляционно заявляя, что опыт не проводился. Вы тоже вдарилиь в формулы, а мне кажется, что просто надо взгляуть открыто на реальность.
#61648 Желя :Теперь я постараюсь объяснить свою точку зрения. Она основана не на формулах а, на эксперименте, объясняющем притяжение тел. Это изменённый опыт Кавендиша, в котором горизонтальная сила взаимодействия масс, действующая на крутильные весы после изменения её человеком, заменена на естественное изменение вертикальных сил притяжения и Архимеда. Этот эксперимент выявил отсутствие горизонтальных сил притяжения масс при явном наличии таких же вертиальных сил. Возник естественный вопрос: массы тел не могут притягиваться вертикально, не притягиваясь горизонтально и наоборот, если массы тел притягивются вертикально, то как существует механизм, который не притягивает массы горизонтально?
zam этот ксперимент не расматривает, безапелляционно заявляя, что опыт не проводился. Вы тоже вдарилиь в формулы, а мне кажется, что просто надо взгляуть открыто на реальность.
Уважаемый Желя, физики, в сущности, это такие козлы, вроде меня, которые не понимают и не представляют, что такие горизонтальные и вертикальные силы и к тому же у них привычка всякое словестное словоблудие рассматривать через некие формулы, ещё лучще через расчёты подтверждённые опытами. Так что, то что делал и проделывал Кавендиш опишите через формулы и прибавьте туда расчёты. Вот такой вот открытый взгляд у физиков на рельность. Желаю удачи.
Уважаемый Хуснулла, теперь я Вас не понимаю. В файле №61591 я сделал вывод формулы, по которой можно вычислить центробежное ускорение. Подставляйте значения и вычисляйте. Что мешает? Непонятен вывод? Вам возможно, так как я его сделал с использованием производных по времени. На словах могу только повторить объяснение. Двигаясь по касательной, Луна убегает от Земли, но Земля своим притяжением возвращает ее на тот же радиус. Ускорение g для Луны Вы многократно вычисляли. Подставив значения скорости Луны и ее радиус в формулу для центробежного ускорения, Вы убедитесь, что оба ускорения равны по величине. Вы же знаете и расстояние от Луны до Земли и скорость Луны. Что за фокусы с Вашей стороны? Таков закон движения по кругу. Если по какой-то причине ускорения станут не равны друг-другу, то Луна уйдет с круговой траектории — или начнет приближаться к Земле, или улетит в далекий космос.