Задача про рамку и шарик на импульс

Опять же тестирую сложность и решаемость, так как составлял сам.
На гладком столе лежит квадратная рамка массой 3 m и стороной a. Внутри рамки на середине стороны начинает движение под углом 45 со скоростью V маленький шарик массой m . Определите перемещение шарика по столу к моменту третьего удара об рамку. Удары абсолютно упругие.


Есть ли трение ?
Какой радиус шарика? Ему же нужно раскручиваться при наборе скорости после удара.
Сколько времени длится удар ? Даже абсолютно упругий удар может длится во времени разное количество времени.
На середине рамки — точка касания ? А если радиус шара в 1000 раз больше a ? Или радиус шарика близок к a ?
Надо знать где центр масс шарика ?
По идеально гдадкому столу сможет ли шарик катится или будет всегда проскальзывать и оставаться на одном месте ?
Точка удара будет ли на геометрической плоскости симметрии шарика. Начертите задачу в проекционном виде, а то не понятно как ударяется шарик.
Рамка квадратная в сечении или круглая или может быть шестигранная ?

#54058 givigudze :Есть ли трение ?
на гладком столе, рамка тоже гладкая, и шарик и воздуха тоже нет. трения нет вобщем
Какой радиус шарика? Ему же нужно раскручиваться при наборе скорости после удара.
шарик маленький (радиусом пренебрегаем)
Сколько времени длится удар ? Даже абсолютно упругий удар может длится во времени разное количество времени.
для чего эта информация?
На середине рамки — точка касания ? А если радиус шара в 1000 раз больше a ? Или радиус шарика близок к a ?
см. выше
Надо знать где центр масс шарика ?
шарик и рамка однородные
По идеально гдадкому столу сможет ли шарик катится или будет всегда проскальзывать и оставаться на одном месте ?
не понял вопрос
Точка удара будет ли на геометрической плоскости симметрии шарика. Начертите задачу в проекционном виде, а то не понятно как ударяется шарик.
шарик маленький
Рамка квадратная в сечении или круглая или может быть шестигранная ?
стенки рамки плоские выше радиуса шарика

#54056 Lucas :Опять же тестирую сложность и решаемость, так как составлял сам.
На гладком столе лежит квадратная рамка массой 3 m и стороной a. Внутри рамки на середине стороны начинает движение под углом 45 со скоростью V маленький шарик массой m . Определите перемещение шарика по столу к моменту третьего удара об рамку. Удары абсолютно упругие.
Хорошая задача!
Сначала она мне показалась чрезвычайно сложной. Мне почудилось, что уже второе столкновение шара со стенкой будет не по центру стенки, а со смещением. Это привело бы к вращению рамки, расчёт получился бы очень трудоёмким.
А потом до меня дошло – при абсолютно упругом ударе скорость сближения тел до столкновения равна скорости разбегания тел после столкновения.
Поэтому в системе отсчёта рамки ( неинерциальной!) траектория шара будет такой:
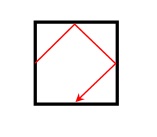
Скорость шара постоянна по величине.
Поэтому время движения шара равно \(t= \frac {3 \sqrt 2}{2} \frac a v\).
Перемещение шара в этой системе отсчёта тоже находится элементарно \((a \frac {\sqrt 2} {2})\). Но ведь нам нужно не это, а перемещение шара в системе отсчёта стола.
Пусть масса шара равна \(m\) , а масса рамки равна \(M\) .
В системе отсчёта стола центр масс системы «рамка+шар» движется равномерно-прямолинейно со скоростью \(v_{ц.м.}=v \frac {m}{M+m}\) и за время t проходит расстояние \(s= \frac {3 \sqrt 2}{2} \frac {m}{M+m}a\).
Теперь нужно найти расстояние от шара до центра масс.
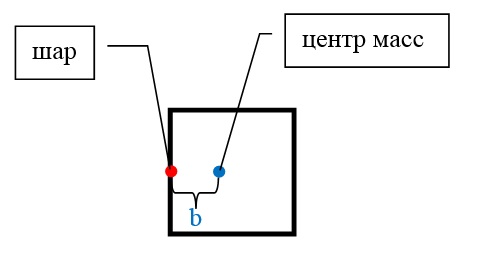
Это элементарно: \(b= \frac a 2 \frac {M}{M+m}\) .
Ну а теперь решение:
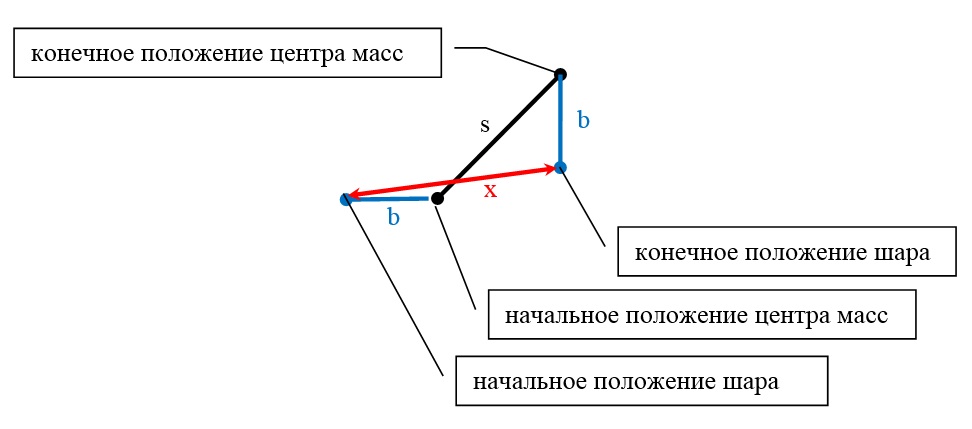
Перемещение шара относительно стола: \(x=\sqrt{\left (s\frac{\sqrt{2}}{2}+b \right )^2+\left (s\frac{\sqrt{2}}{2}-b \right )^2}=\sqrt{s^2+2b^2}=a\frac{\sqrt{2M^2+18m^2}}{2\left ( M+m \right )}\) .
Если, как задано в условии, \(M=3m\), то \(x= \frac 3 4 a\).
А у вас какой ответ.
Задача как раз для олимпиады. Нужно кое о чём догадаться, а потом элементарные вычисления.
Ну а вот ещё иллюстрация — как двигаются шар и рамка в системе отсчёта стола.
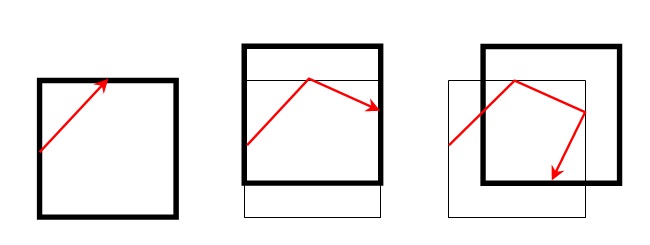
отредактировал(а) zam: 2022-12-20 15:16 GMT

#54077 zam :#54056 Lucas :Опять же тестирую сложность и решаемость, так как составлял сам.
На гладком столе лежит квадратная рамка массой 3 m и стороной a. Внутри рамки на середине стороны начинает движение под углом 45 со скоростью V маленький шарик массой m . Определите перемещение шарика по столу к моменту третьего удара об рамку. Удары абсолютно упругие.
Хорошая задача!
Сначала она мне показалась чрезвычайно сложной. Мне почудилось, что уже второе столкновение шара со стенкой будет не по центру стенки, а со смещением. Это привело бы к вращению рамки, расчёт получился бы очень трудоёмким.
да, я ограничился с квадратной рамкой и ударом под 45, иначе было бы вращение… это уже слишком сложно.
А потом до меня дошло – при абсолютно упругом ударе скорость сближения тел до столкновения равна скорости разбегания тел после столкновения.
Поэтому в системе отсчёта рамки ( неинерциальной!) траектория шара будет такой:
У меня было больше всего сомнений именно в этом предположении, так как удар под углом, а в остальном решение совпадает.

Скорость шара постоянна по величине.
Поэтому время движения шара равно \(t= \frac {3 \sqrt 2}{2} \frac a v\).
Перемещение шара в этой системе отсчёта тоже находится элементарно \((a \frac {\sqrt 2} {2})\). Но ведь нам нужно не это, а перемещение шара в системе отсчёта стола.
Пусть масса шара равна \(m\) , а масса рамки равна \(M\) .
В системе отсчёта стола центр масс системы «рамка+шар» движется равномерно-прямолинейно со скоростью \(v_{ц.м.}=v \frac {m}{M+m}\) и за время t проходит расстояние \(s= \frac {3 \sqrt 2}{2} \frac {m}{M+m}a\).
Теперь нужно найти расстояние от шара до центра масс.

Это элементарно: \(b= \frac a 2 \frac {M}{M+m}\) .
Ну а теперь решение:

Перемещение шара относительно стола: \(x=\sqrt{\left (s\frac{\sqrt{2}}{2}+b \right )^2+\left (s\frac{\sqrt{2}}{2}-b \right )^2}=\sqrt{s^2+2b^2}=a\frac{\sqrt{2M^2+18m^2}}{2\left ( M+m \right )}\) .
Если, как задано в условии, \(M=3m\), то \(x= \frac 3 4 a\).
А у вас какой ответ.
Задача как раз для олимпиады. Нужно кое о чём догадаться, а потом элементарные вычисления.
Ну а вот ещё иллюстрация — как двигаются шар и рамка в системе отсчёта стола.
а это как построили? в программе какой-то, или просто аналитически считали скорость рамки и шарика отн стола?

Если трение отсутствует, то получилось примерно так:

«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2022-12-21 14:12 GMT

Для условия задачи, наверное лучше подойдёт не шарик, а шайба. Шарик подразумевает качение, а если трения нет, то качение как то не логично. А если всё таки — качение, тогда после соударения с рамкой он должен будет поменять направление качения, а значит — должна поменять своё положение в пространстве (эффект гироскопа) ось вращения шарика, — что усложняет задачу.
Шайба не должна получить вращающий момент после соударения, т.е., соударение должно быть тоже без трения, иначе будет другая картина движений.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2022-12-21 11:24 GMT

#54077 zam :
Ну а вот ещё иллюстрация — как двигаются шар и рамка в системе отсчёта стола.

Какая сила остановила движение рамки вперёд?
После второго столкновения рамка должна начать движение вбок (вправо), но и движение вперёд продолжается с постоянной скоростью, в то время как скорость шарика после второго столкновения (передачи части импульса рамке), уменьшилась.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2022-12-22 10:55 GMT

Valery Z согласен.

#54079 Lucas :а это как построили? в программе какой-то, или просто аналитически считали скорость рамки и шарика отн стола?
Никак не построил, ничего не считал. Просто в графредакторе нарисовал эскиз (иллюстрацию). К тому же, неточно нарисовал. Нужно так:
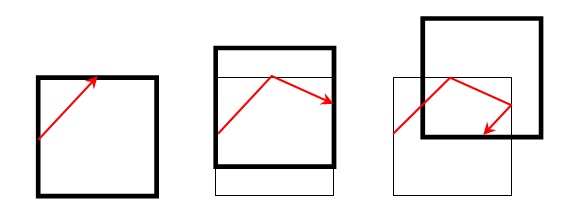

#54143 zam :#54079 Lucas :а это как построили? в программе какой-то, или просто аналитически считали скорость рамки и шарика отн стола?
Никак не построил, ничего не считал. Просто в графредакторе нарисовал эскиз (иллюстрацию). К тому же, неточно нарисовал. Нужно так:

А почему при втором соударении углы падения и отражения равны? Рамка принимает часть импульса от шарика, начинает двигаться, и шарик должен отскочить под другим углом, — как после первого соударения. Или нет?...
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков

#54149 Valery Z :А почему при втором соударении углы падения и отражения равны?
Потому что это эскиз.
У вас какой ответ?

#54150 zam :#54149 Valery Z :А почему при втором соударении углы падения и отражения равны?
Потому что это эскиз.
У вас какой ответ?
У меня получается, что после второго соударения шарик и рамка движутся навстречу друг другу, поэтому, до середины рамки шарик не успевает докатиться.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков

#54151 Valery Z :У меня получается, что после второго соударения шарик и рамка движутся навстречу друг другу, поэтому, до середины рамки шарик не успевает докатиться.
Какой ответ у вас получился?

#54152 zam :#54151 Valery Z :У меня получается, что после второго соударения шарик и рамка движутся навстречу друг другу, поэтому, до середины рамки шарик не успевает докатиться.
Какой ответ у вас получился?
Мои предположения оказались не верными. Шарик всегда будет соударяться с серединой каждой из сторон рамки.
Перемещение у меня получилось (11/16) а.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2022-12-31 16:01 GMT

#54200 Valery Z :Перемещение у меня получилось (11/16) а.
То есть, у меня ошибка? А где?

#54207 zam :#54200 Valery Z :Перемещение у меня получилось (11/16) а.
То есть, у меня ошибка? А где?
С чего вы взяли, что у вас ошибка?
Я такого не говорил. Ошибка может у меня...
Я исхожу из того, что в промежутке времени между первым и вторым ударами рамка переместилась на (1/6) а, а шарик отскочил на (1/3) а вдоль оси ОY.
Не очень понятно расположение начальной и конечной точек ц. масс, и перемещение (Х) на рисунке.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков
отредактировал(а) Valery Z: 2023-01-01 13:54 GMT

#54152 zam :#54151 Valery Z :У меня получается, что после второго соударения шарик и рамка движутся навстречу друг другу, поэтому, до середины рамки шарик не успевает докатиться.
Какой ответ у вас получился?
Разобрался, ответ получился такой же как у вас.
Сначала решил считать по пропорциям масс, взяв за основу полную передачу импульса при варианте равных масс, когда шарик, передав импульс рамке, двигаясь по оси ОХ останавливается, а рамка начинает двигаться со скоростью шарика до удара. Значит (логически) при соотношении масс 1:2 рамка получит скорость 1/2, а шарик отскочит со скоростью 1/2 по оси ОХ от первоначальной своей скорости. А при соотношении 1:3, соответственно — рамка получит 1/3, а шарик отскочит на 2/3 по оси ОХ. Но, оказалось, что такая логика ошибочна. Посчитал импульсы по формуле — всё сошлось с вашим ответом.
P.s. Вектор перемещения шарика получился чётко параллельный оси ОХ.
«Многие вещи нам непонятны не потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий». © Козьма Прутков




