Задачи про проводящие сферы

Решил тут я помочь дочке по физике — да и для собственного удовольствия поразмять мозги, вспомнить былое — порешать непростые задачи по физике. И понял — что я физику на самом то деле совершенно не понимаю.
Набросаю в этой теме несколько задач с проводящими сферами в электростатике — хотелось бы увидеть ваши объяснения
Вот задача из демонстарционного варианта ФИПИ ЕГЭ по физике на 2023 год.
«В нижней половине незаряженного металлического шара располагается крупная шарообразная полость,
заполненная воздухом. Шар находится в воздухе вдали от других предметов. В центр полости
помещён положительный точечный заряд q > 0 (см. рисунок). Нарисуйте картину линий
напряжённости электростатического поля внутри полости, внутри проводника и снаружи шара. Если
поле отсутствует, напишите в данной области:
 = 0.
= 0.
Если поле отлично
от нуля, нарисуйте картину поля в данной области, используя восемь линий напряжённости. Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.»
Дано решение задачи:
"
картины линий напряжённости: внутри полости – семейство прямых лучей,
исходящих из заряда и приходящих на поверхность полости по нормали;
снаружи шара – семейство прямых лучей, исходящих с поверхности шара
по нормали к ней и уходящих в бесконечность.
2. Внутри проводника – электростатическое поле
 = 0.
= 0.
3. Заряд q помещён в центр шарообразной полости, поэтому его электростатическое поле в полости обладает
центральной симметрией и выглядит как поле уединённого точечного заряда
q > 0, находящегося в центре полости. Линии напряжённости этого поля
подходят по нормали к поверхности полости, где равномерно распределён
отрицательный индуцированный заряд −q < 0.
4. На наружной поверхности шара находится (в силу нейтральности шара
в целом) положительный заряд q > 0. Поскольку внутри проводника
 = 0,
= 0,
а снаружи окружающие предметы расположены далеко от шара, этот заряд
распределён по поверхности шара равномерно. Его поле вне шара выглядит
как поле уединённого точечного заряда q > 0, расположенного в центре
шара. Линии напряжённости отходят от шара по нормали к его поверхности"
Так вот — непонятны след рассуждения — так как заряд помещен в центр полости, то его поле центрально-симметрично. НО ведь сама полость НЕ центрально симметрична относительно шара!
Где доказательства того, что не симметричное расположение полости не влияет на симметричность поля внутри этой полости?? А вдруг индуцированные заряды не симметричны и соответственно искажают симметрию поля внутри полости?
Далее — такое рассуждение у авторов задачи — «Поскольку внутри проводника
 = 0,
= 0,
а снаружи окружающие предметы расположены далеко от шара, этот заряд
распределён по поверхности шара равномерно» .
А как конкретно то эти факты связаны?? помнится в одном из учебников физики рассказывалось о ситуации на остриях заряженных проводников — там идет скопление заряда, точнее плотность заряда высокая и потому то с этих концов может происходить искрение изза тогог, что заряд отрывается от поверхности проводника изза сильного поля. То есть равенство нулю эл поля внутри проводника никоим образом не делало распределение заряда равным по поверхности.
П.С. Если есть ссылка на какой нибудь источник, где бы хорошо, четко и однозначно бы объяснялись процессы распределения зарядов в проводящих сферах — буду благодарен
Нашел вроде одну на вид неплохую — из кванта. Но там к примеру такое объяснение задачи (Черноуцан «Практикум абитуриента») -
«Задача 5. Проводящая сфера радиусом R заряжена зарядом Q. Каким
станет потенциал сферы, если на расстоянии l от ее центра поместить
точечный заряд q? Разобрать случаи
l > R и l < R.
»
вот выдержка из решения:
" Перейдем к случаю l < R (рис. 6). Так как теперь заряд находится внутри
сферы, напряженность поля внутри сферы не равна нулю и потенциалы
различных точек не равны друг другу. Однако и в этом случае несложно определить потенциал сферы, только надо
обратить внимание не на внутреннюю часть сферы, а на окружающее ее внешнее пространство. Оказывается, поле
во внешнем пространстве не зависит от положения заряда q внутри сферы, т.е.
при перемещении заряда по внутренней области поле во внешней области
не меняется.
Это утверждение верно для полого
проводника любой формы, и следует
оно из теоремы единственности. Поле
во внешнем пустом пространстве однозначно определяется следующими
условиями: 1) потенциал на бесконечности равен нулю; 2) потенциал на
поверхности проводника принимает некоторое постоянное значение; 3) полный заряд внутри этой поверхности
известен, т.е. известно полное число
силовых линий, начинающихся на поверхности проводника. Существует
единственное поле, удовлетворяющее
этим условиям.
"
То есть говорится что «поле
во внешнем пространстве не зависит от
положения заряда q внутри сферы, т.е.
при перемещении заряда по внутренней области поле во внешней области
не меняется.
Это утверждение верно для полого
проводника любой формы, и следует
оно из теоремы единственности»
НО не показывается, не объясняется как оно из этого следует!

deleted
Причина: флуд.
отредактировал(а) zam: 2022-08-31 18:53 GMT

#51096 iliaborisov :То есть говорится что «поле
во внешнем пространстве не зависит от
положения заряда q внутри сферы, т.е.
при перемещении заряда по внутренней области поле во внешней области
не меняется.
Это утверждение верно для полого
проводника любой формы, и следует
оно из теоремы единственности»
НО не показывается, не объясняется как оно из этого следует!
Так теорема именно это и объясняет.
А вы знаете, что это такое — теорема о единственности решения электростатической задачи? Вот она: Теорема единственности .
Давайте попробую словами.
Главное во всей этой истории то, что шар металлический, то есть, хороший проводник. Это значит, что в статике все точки шара имеют один и тот же потенциал (иначе в шаре был бы электрический ток, что противоречит тому, что задача по электростатике). Значит, и внешняя поверхность шара, и поаерхность шарообразной полости являются эквипотенциальными поверхностими. А линии напряжённости поля перпендикулярны эквипотенциальным поверхностям (поверхностям равного потенциала). Потому что напряженность — это градиент потенциала (с противоположным знаком).
Ну а линии, перпендикулярные поверхности шара — это радиусы шара.
Если мы будем двигать заряд внутри полости, то это приведёт к тому, что изменится распределение заряда на поверхности шара. И распределится он именно так, чтобы поле снаружи шара не изменилось (в полости поле, конечно, изменится).
отредактировал(а) zam: 2022-09-01 14:51 GMT

Если заряд статический то ток никуда не течет. Сам заряд по металлическим телам распределяется равномерно по поверхности. Из центра заряд выталкивается на поверхность.
Не забывем про клетку Фарадея.
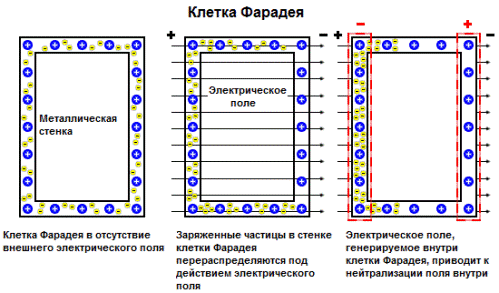
Но клетка Фарадея действует и наоборот, когда мы в неё поместим заряд, который с ней не контактирует.
Наглядкая картинка о нелинейности процесса распределения силовых линий электрического поля.
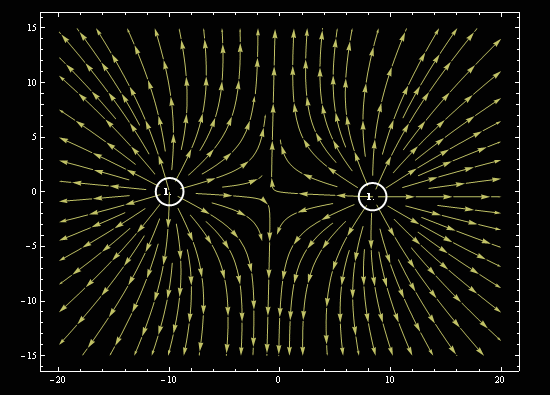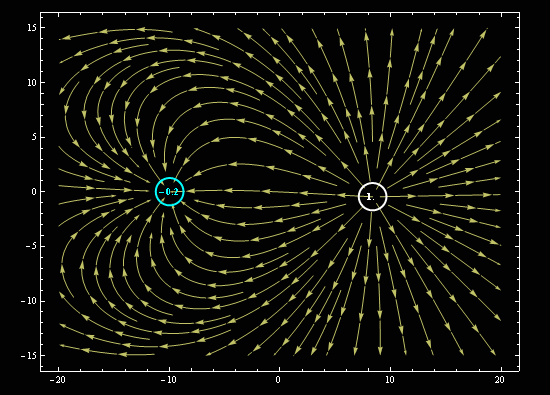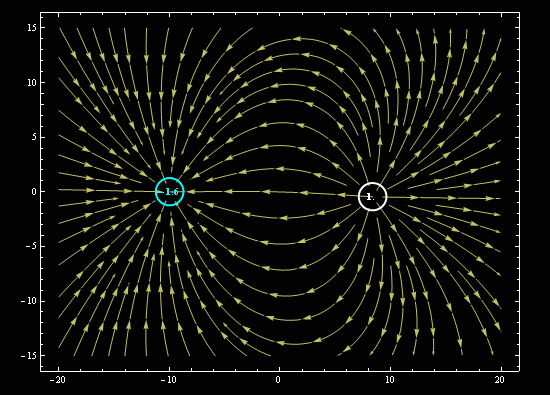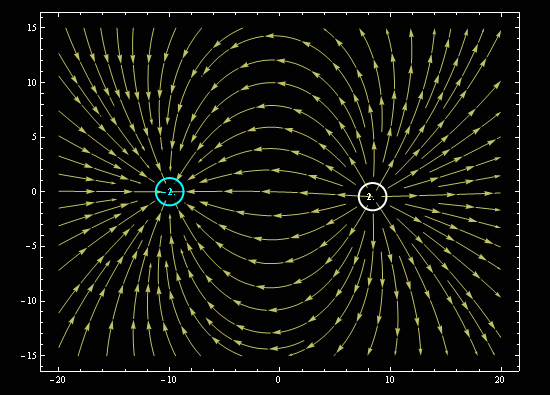

#51124 zam :Так теорема именно это и объясняет.
А вы знаете, что это такое — теорема о единственности решения электростатической задачи? Вот она: Теорема единственности .
Давайте попробую словами.
Главное во всей этой истории то, что шар металлический, то есть, хороший проводник. Это значит, что в статике все точки шара имеют один и тот же потенциал (иначе в шаре был бы электрический ток, что противоречит тому, что задача по электростатике). Значит, и внешняя поверхность шара, и поаерхность шарообразной полости являются эквипотенциальными поверхностими. А линии напряжённости поля перпендикулярны эквипотенциальным поверхностям (поверхностям равного потенциала). Потому что напряженность — это градиент потенциала (с противоположным знаком).
Ну а линии, перпендикулярные поверхности шара — это радиусы шара.
Если мы будем двигать заряд внутри полости, то это приведёт к тому, что изменится распределение заряда на поверхности шара. И распределится он именно так, чтобы поле снаружи шара не изменилось (в полости поле, конечно, изменится).
Все равно остается непонятным. Если вы ВНЕ шара расположите заряд — то распределение заряда — что индуцированного что собственного будет СИЛЬНО зависеть от расположения заряда. Причем вне зависимости от расположения — и линии ВСЕ равно будут перпендикулярными и эквипотенциальность сохраняется. Так что они тут непосредственно ни при чем. И Кстати — /Вы пишете " Если мы будем двигать заряд внутри полости, то это приведёт к тому, что изменится распределение заряда на поверхности шара. И распределится он именно так, чтобы поле снаружи шара не изменилось"
А в ответе — следующее «Поскольку внутри проводника
 = 0,
= 0,
а снаружи окружающие предметы расположены далеко от шара, этот заряд
распределён по поверхности шара равномерно»
Конкретно почему распределение заряда то равномерное? Или оно не равномерное, а равномерное только поле вне шара?

НУ очень много вопросов. Может быть начать с одного.
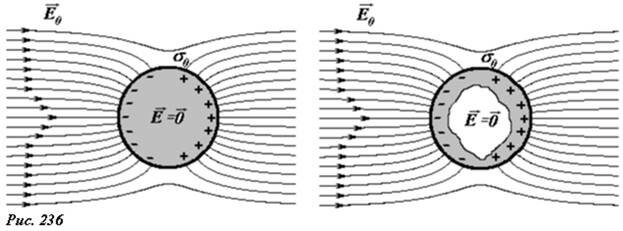
Как видите у сферы есть заряд и он не равномерный, если сфера под действием электричесого поля. Но силовые линии из сферы выходят перпендикулярно поверхности сферы.
Если же мы одарили сферу зарядом, а внешнее поле равно нулю, то весь заряд равномерно распределится по поверхности сферы.
заряд внутри сферы
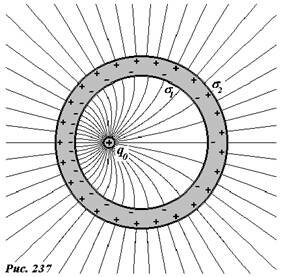
Хотя в этой картинке есть вопрос, что же такое может быть что разделяет заряды в проводнике. Почему нет тока от поверхности сферы к её центру. Но ответ тоже есть — поле заряда помещенного внутрь сферы. Но вопрос все же остается — если мы закрыли заряд сферой, дотронулись до неё — то к нам перешел заряд сферы ? Что то мне подсказывет, что на поверхности сферы сила поля будет гораздо меньше чем внутри сферы.
не прав был я что клетка фарадея работает наоборот. Всему виной закон сохранения заряда.
Подчеркнем, что сплошная металлическая оболочка экранирует электрическое поле, находящееся снаружи от оболочки, но не те, которые находятся внутри нее. Пусть точечный заряд +q0 находится внутри металлической сферической оболочки (рис. 237). Этот заряд создает электрическое поле, которое индуцирует электрические заряды, как на внутренней, так и на внешней поверхностях оболочки. Рассмотрим, как в этом случае изменится распределение электрического поля.
На внутренней поверхности распределятся отрицательные заряды с некоторой поверхностной плотностью σ1. Внутри металла напряженность поля равна нулю, поэтому отрицательные индуцированные заряды σ1 полностью экранируют поля заряда q0. Используя теорему Гаусса, легко показать, что суммарный заряд, индуцированный на внутренней поверхности, равен -q0. Суммарный заряд оболочки остается равным нулю, следовательно, на ее внешней поверхности индуцируется положительный заряд равный +q0. На поверхностное распределение этого заряда σ2, заряды внутренней поверхности и заряд полости не действуют, поэтому они распределятся по поверхности оболочки равномерно, и вне оболочки будут создавать электрическое поле эквивалентное полю точечного заряда +q0, помещенного в центр сферической оболочки. Подчеркнем такое распределение поля вне оболочки не зависит от положения заряда внутри полости – смещение этого заряда приведет к изменению поля внутри полости, изменению распределения зарядов на внутренней поверхности, но не изменяет поля вне оболочки.
Чтобы «убрать» поле снаружи от оболочки ей необходимо сообщить дополнительный отрицательный заряд, такого эффекта можно добиться, заземлив оболочку.
отредактировал(а) givigudze: 2022-09-01 19:15 GMT

#51163 givigudze :Сам заряд по металлическим телам распределяется равномерно по поверхности.
Только если поверхность металлического тела сферическая. Иначе — неравномерно. На выпуклостях (особенно остриях) плотность заряда максимальная На впадинах — минимальная. Поэтому огни Сятого Эльма зажигаются на кончиках мачт и рей. Поэтому концы молниеотводов заостряют.
Не забывем про клетку Фарадея.

Тут всё верно.
Но клетка Фарадея действует и наоборот, когда мы в неё поместим заряд, который с ней не контактирует.
А это не понятно.

#51165 iliaborisov :Если вы ВНЕ шара расположите заряд — то распределение заряда — что индуцированного что собственного будет СИЛЬНО зависеть от расположения заряда. Причем вне зависимости от расположения — и линии ВСЕ равно будут перпендикулярными и эквипотенциальность сохраняется.
Да, всё так. Только силовые линии уже не будут прямолинейными. И густота их будет переменной (где плотность заряда выше, там линии гуще).
И ещё. Никакого индуцированного заряда не бывает. Только собсвенный. Индуцрованным бывает электрическое поле.
И Кстати — /Вы пишете " Если мы будем двигать заряд внутри полости, то это приведёт к тому, что изменится распределение заряда на поверхности шара. И распределится он именно так, чтобы поле снаружи шара не изменилось"
Я имел в виду внутреннюю поверхность шара (границу шара (металла) и полости внутри шара). (Ведь был же уверен, что это написал; оказывается — не написал).
Эх, видно, картинку рисовать придётся.
Конкретно почему распределение заряда то равномерное? Или оно не равномерное, а равномерное только поле вне шара?
Распределение заряда на внешней поверхности шара — равномерное.
Напряжённось поля в проводнике равна нулю (статика!). Значит, на заряд на поверхности шара (электрон) «изнури» никакая сила не действует. Внешние предметы очень далеко. тоже не действуют. Остаются силы между зарядами на поверхности проводника. Это силы отталкивания. Они стремятся распределить заряды по поверхности сферы равномерно. (Дейсвительно, если где-то возникнет пятно с повышенной плотностью заряда, то на электроны на краю пятна будет действовать сила изнутри пятна больше, чем сила снаружи (с той стороны, где концентрация электронов меньше). Пятно рассосётся.

#51187 givigudze :

Ну вот! Есть картинка, мне рисовать не пришлось.
Хотя в этой картинке есть вопрос, что же такое может быть что разделяет заряды в проводнике.
Поле внутреннего заряда.
Почему нет тока от поверхности сферы к её центру.
Потому что нет разницы потенциалов.
Но вопрос все же остается — если мы закрыли заряд сферой, дотронулись до неё — то к нам перешел заряд сферы ?
Вы станете заряжены положительно. Сфера станет заряжена отрицательно. Закон сохранения электрического заряда.
Что то мне подсказывет, что на поверхности сферы сила поля будет гораздо меньше чем внутри сферы.
Смотрите на картинку. Где силовые линии гуще, там сила (а точнее — напряжённость) поля больше.
отредактировал(а) zam: 2022-09-02 08:11 GMT

#51187 givigudze :
На внутренней поверхности распределятся отрицательные заряды с некоторой поверхностной плотностью σ1. Внутри металла напряженность поля равна нулю, поэтому отрицательные индуцированные заряды σ1 полностью экранируют поля заряда q0. Используя теорему Гаусса, легко показать, что суммарный заряд, индуцированный на внутренней поверхности, равен -q0. Суммарный заряд оболочки остается равным нулю, следовательно, на ее внешней поверхности индуцируется положительный заряд равный +q0. На поверхностное распределение этого заряда σ2, заряды внутренней поверхности и заряд полости не действуют, поэтому они распределятся по поверхности оболочки равномерно, и вне оболочки будут создавать электрическое поле эквивалентное полю точечного заряда +q0, помещенного в центр сферической оболочки. Подчеркнем такое распределение поля вне оболочки не зависит от положения заряда внутри полости – смещение этого заряда приведет к изменению поля внутри полости, изменению распределения зарядов на внутренней поверхности, но не изменяет поля вне оболочки.
Чтобы «убрать» поле снаружи от оболочки ей необходимо сообщить дополнительный отрицательный заряд, такого эффекта можно добиться, заземлив оболочку.
Понял, Большущее спасибо! Я чтото затупил — пытался представить, что поле внутри металлической части шара равно нулю только засчет трех слоев заряда. А оно нулю засчет двух внутренних и таким образом — да, на поверрхностные заряды внутренние слои не действуют, «обнуляя» себя. А поверхностные тоже дают ноль внутри.
отредактировал(а) iliaborisov: 2022-09-02 12:48 GMT

#51199 zam :Но клетка Фарадея действует и наоборот, когда мы в неё поместим заряд, который с ней не контактирует.
А это не понятно.
Ну да, это противоречит Гауссу — поток же вне клетки не будет равен нулю, т.е. поле будет ненулевым.

Хм, все же подумав — извиняюсь за свою въедливость -нашел небольщой изъян в этих рассуждениях.
Итак — повторим цепочку рассуждений… Из равенства нулю поля в толще проводника (при любом расположении любых зарядов — хотя еще будучи школьником понял что это может быть не всегда так — но это вопрос не имющий отношения к ситуации) -> поток -согласно Гауссу-равен нулю (через поверхность охватывающую заряд точечный в полости q0 и индуцируемые им заряды на поврехности этой полости σ1) -> сумма зарядов равна тоже нулю. По этот момент я согласен. НО далее делается сомнительный с точки зрения строгости вывод, что и поле, создаваемое суммарно этим положит точечным зарядом q0 и индуцированным отриц зарядом на поверхности полости (не шара!) σ1 в пространстве во вне по отношению поверхности полости (к примеру в толще проводника или на поверхности шара) тоже будет нулевым
А вот элементарный пример — берем диполь, окружаем его произвольной — можно сферической можно не сферической — поверхностью (гипотетической, нематериальной) — и да — ГАусс дает поток ноль. А вот поле ни фига не нулевое! Так что просто на основании суммы заряда и потока нельзя говорить, что поле создаваемое суммарно нулевыми зарядами будет тоже ноль.
А ведь именно на основании этого довода — что заряд Q и заряды сигма1 дают вне себя нулевое поле — мы делаем вывод, что внешний заряд на шаре будет гарантированно равномерен — ибо на него не действует внутреннее поле, т.к. оно равно нулю
отредактировал(а) iliaborisov: 2022-09-02 13:59 GMT

#51241 iliaborisov :Итак — повторим цепочку рассуждений…
Давайте. Аккуратно, не торопясь.
Из равенства нулю поля в толще проводника (при любом расположении любых зарядов — хотя еще будучи школьником понял что это может быть не всегда так — но это вопрос не имющий отношения к ситуации)
«Из равенства нулю поля». Нужно говорить так: «Из равенства нулю напряжённости поля». Вы же это имеете в виду? Равенство напряженности нулю не означает отсутствия поля. Ведь потенциал там совсем не обязательно равен нулю.
В статике напряжённость поля в проводнике равна нулю всегда. Заряды расположатся именно так, чтобы напряженность была равной нулю.
-> поток -согласно Гауссу-равен нулю (через поверхность охватывающую заряд точечный в полости q0 и индуцируемые им заряды на поврехности этой полости σ1)
Нет. Это не следует из предыдущего. Поток вектора напряженности через замкнутую поверхность равен заряду, окружённому этой поверхностью (с точностью до коэффициента).
-> сумма зарядов равна тоже нулю.
Ну как же она равна нулю? В полости есть заряд. Шар в целом не заряжен (заряд на внешней поверхности равен и противоположен по знаку заряду на внутренней поверхности и они по модулю равны заряду в полости). Так что, сумма зарядов не ноль, а равна заряду в полости.
По этот момент я согласен. НО далее делается сомнительный с точки зрения строгости вывод, что и поле, создаваемое суммарно этим положит точечным зарядом q0 и индуцированным отриц зарядом на поверхности полости (не шара!) σ1 в пространстве во вне по отношению поверхности полости (к примеру в толще проводника или на поверхности шара) тоже будет нулевым
Такого вывода не делается. Нельзя сделать такой вывод. Теорема Гаусса — она про полный поток через поверхность. Равенство нулю полного потока не означает, что вектор напряженности на всех участках поверхности равен нулю. Он может быть не нулев и направлен как «внутрь», так и «наружу».
В толще проводника напряжённость равна нулю по той причине, что иначе в проводнике будет электрический ток (плотность электрического тока пропорциональна напряжённости электрического поля — закон Ома). А у нас статика — никаких токов.
А вот элементарный пример — берем диполь, окружаем его произвольной — можно сферической можно не сферической — поверхностью (гипотетической, нематериальной) — и да — ГАусс дает поток ноль.
Да.
А вот поле ни фига не нулевое!
А напряженность поля не нулевая. Положительный, отрицательный заряд диполя даёт поток вектрора напряжённости вовнутрь. Суммарный поток — ноль.
Так что просто на основании суммы заряда и потока нельзя говорить, что поле создаваемое суммарно нулевыми зарядами будет тоже ноль.
Никто этого и не гоаорит.
А ведь именно на основании этого довода — что заряд Q и заряды сигма1 дают вне себя нулевое поле — мы делаем вывод, что внешний заряд на шаре будет гарантированно равномерен — ибо на него не действует внутреннее поле, т.к. оно равно нулю
Нет. Я вам дал другое объяснение равномерного распределения заряда на внешней поверхности шара.

#51247 zam :Из равенства нулю поля в толще проводника (при любом расположении любых зарядов — хотя еще будучи школьником понял что это может быть не всегда так — но это вопрос не имющий отношения к ситуации)
«Из равенства нулю поля». Нужно говорить так: «Из равенства нулю напряжённости поля». Вы же это имеете в виду? Равенство напряженности нулю не означает отсутствия поля. Ведь потенциал там совсем не обязательно равен нулю.
Ну я конечно же имел ввиду да — напряженность.
В статике напряжённость поля в проводнике равна нулю всегда. Заряды расположатся именно так, чтобы напряженность была равной нулю.
Оффтоп. но я еще — как писал — в школе придумал вариант, когда это не будет. Да, электроны металла под воздействием внешнего поля выстраиваются так, что полностью скомпенсирують внешнее поле. Но надо же понимать, что максимально возможное «ответное» поле (напряженность) определяется количеством электронов (скорее всего даже не всех, а только проводимости) которое есть в этом куске металла. А оно не бесконечное. поэтому если поместить кусок металла в такое сильное поле, которое будет больше того, что могут создать все электроны данного куска металла, то напряженность поля внутри понятное дело не будет равно нулю — просто не хватит электронов, чтобы полностью скомпенсировать огромное внешнее поле. Но это так, оффтоп
-> поток -согласно Гауссу-равен нулю (через поверхность охватывающую заряд точечный в полости q0 и индуцируемые им заряды на поврехности этой полости σ1)
Нет. Это не следует из предыдущего. Поток вектора напряженности через замкнутую поверхность равен заряду, окружённому этой поверхностью (с точностью до коэффициента).
Следует. Если напряженность везде по границе поверхности равна нулю (а она равна нулю в проводнике), то и сам поток, которые есть интеграл произведения скалярного Е на площадь тоже равен нулю так как Е=0
-> сумма зарядов равна тоже нулю.
Ну как же она равна нулю? В полости есть заряд. Шар в целом не заряжен (заряд на внешней поверхности равен и противоположен по знаку заряду на внутренней поверхности и они по модулю равны заряду в полости). Так что, сумма зарядов не ноль, а равна заряду в полости.
ИМеется ввиду q0 и σ1 в обозначениях givigudze — так как мы берем замкнутую поверхность, охватывающую только q0 и σ1, но не σ2
По этот момент я согласен. НО далее делается сомнительный с точки зрения строгости вывод, что и поле, создаваемое суммарно этим положит точечным зарядом q0 и индуцированным отриц зарядом на поверхности полости (не шара!) σ1 в пространстве во вне по отношению поверхности полости (к примеру в толще проводника или на поверхности шара) тоже будет нулевым
Такого вывода не делается. Нельзя сделать такой вывод. Теорема Гаусса — она про полный поток через поверхность. Равенство нулю полного потока не означает, что вектор напряженности на всех участках поверхности равен нулю. Он может быть не нулев и направлен как «внутрь», так и «наружу».
С этим абсолютно согласен

Нет. Я вам дал другое объяснение равномерного распределения заряда на внешней поверхности шара.
Вы дали такое — "
Распределение заряда на внешней поверхности шара — равномерное.
Напряжённось поля в проводнике равна нулю (статика!). Значит, на заряд на поверхности шара (электрон) «изнури» никакая сила не действует. Внешние предметы очень далеко. тоже не действуют. Остаются силы между зарядами на поверхности проводника. Это силы отталкивания. Они стремятся распределить заряды по поверхности сферы равномерно. (Дейсвительно, если где-то возникнет пятно с повышенной плотностью заряда, то на электроны на краю пятна будет действовать сила изнутри пятна больше, чем сила снаружи (с той стороны, где концентрация электронов меньше). Пятно рассосётся."
Тут в моем понимании ключевая фраза «Значит, на заряд на поверхности шара (электрон) «изнутри» никакая сила не действует»
НО то что изнутри никакая сила не действует — это то мы не доказали. Равеноство нулю напряженности поля внутри проводника означает СТРОГО говоря, что СУПЕРПОЗИЦИЯ ПОЛЕЙ от ТРЕХ скоплений заряда — двух слоев заряда -σ1 и σ2 и точечного q0 в толще металла равна нулю (под полем сейчас и далее имею ввиду напряженность, коли это разные понятия). ВЕДЬ если бы мы рассматривали бы ситуацию с внешним посторонним зарядом вне шара, то Вас бы не удивило бы то, что в таком случае сторонний заряд ТАК влияет на распределение внешнего заряда на поверхности металла, что он распределен не равномерно. ХОТЯ внутри этого проводника поле ВСЕ равно остается равным нулю. А вот когда речь заходит о внутренних зарядах — то они почему то не влияют на распределение. Вот это то и непонятно
Ведь поле внутри проводника создается в ТОМ числе и зарядам на поверхности шара — к этому моменту УЖЕ как то распределенному. А не то, что сначала поле внутри проводника становится нулевым, а потом уже идет какое то распределение заряда по поверхности — в таком случае да — УЖЕ сложившиеся НУЛЕВОЕ внутреннее поле НЕ повлияло бы на равномерное распределение зарядо по поверхности
отредактировал(а) iliaborisov: 2022-09-02 16:11 GMT

А если поле изнутри в каждой точке сферы направленно из центра во внешнее пространстрво и никак не мешает электронам вставать в ровные ряды по поверхности сферы ?
Хотя могу выдвинуть такую гипотезу. Что поле именно на поверхности сферы равно нулю, но как только мы чуток внутрь — так оно сразу начинает расти. И нашим бедным электронам некуда дется от этого сильного поля, остается только выстроится на поверхности сферы.
Но дело в том что сами электроны же образуют поле, поэтому там где есть заряды не может быть нулевое поле. Видите внутри сферы то точечный заряд. А наповерхности рапределенный заряд, а в той теории, которую нам дают мы думает о большом массиве электронов. Но теорема Гаусса не оперирует электронами. Нужно так и думать что на сфере один рапределенный заряд.
Я бы не рассматривал в школе такую задачу. Сильно много всего нужно знать. Вот кто из Вас расскажет как распределенно статическое электрическое поле в тоще металла. С каким коэффициентом оно уменьшается, оно же не может оставаться таким же как и было. Вот если мы в толщу диэлектрика между обкладками конденсатора просунем тонкую металлическую пластинку — то емкость уменьшится. Какая минимальная тощина металла в сфере должна быть что бы заряд по внешней поверхности распространялся равномерно при наличии внутри заряда в какой-то точке. Вот сделали мы сферу из нанофольги и ? Ну в общем на практике Вы же понимаете что все не так. А ну сделали мы сферу из графита и ?
Из общей теории и то о чем говорил Гаусс. Металлическая сфера обладает сверхпроводимостью. Изходя из этого и думаем.

#51251 iliaborisov :Оффтоп. но я еще — как писал — в школе придумал вариант, когда это не будет. Да, электроны металла под воздействием внешнего поля выстраиваются так, что полностью скомпенсирують внешнее поле. Но надо же понимать, что максимально возможное «ответное» поле (напряженность) определяется количеством электронов (скорее всего даже не всех, а только проводимости) которое есть в этом куске металла. А оно не бесконечное. поэтому если поместить кусок металла в такое сильное поле, которое будет больше того, что могут создать все электроны данного куска металла, то напряженность поля внутри понятное дело не будет равно нулю — просто не хватит электронов, чтобы полностью скомпенсировать огромное внешнее поле. Но это так, оффтоп
Конечно, рассматриваются только электроны проводимости (свободные электроны). Их количество не бесконечно, но огромно.
Такого сильного поля мы не можем даже близко создать.
Но если бы смогли, то. электроны стали бы выраваться из металла и улетать под действием поля. Это называется электростатическая (автоэлектронная) эмиссия. Кусок металла заряжался бы положительно, в конце концов электростатические силы отталкивания разрушили бы кусок металла (на уровне кристаллической решётки, он перестал бы быть металлом).
Так что, в толще металла напряжённость эллектрического поля равна нулю (в статике).
Следует. Если напряженность везде по границе поверхности равна нулю (а она равна нулю в проводнике), то и сам поток, которые есть интеграл произведения скалярного Е на площадь тоже равен нулю так как Е=0
На поверхности расположен заряженный слой (тонкий, примерно 2-3 межатомных расстояния). Поэтому напряжённость поля ноль в толще проводника, но не ноль на поверхности.

ИМеется ввиду q0 и σ1 в обозначениях givigudze — так как мы берем замкнутую поверхность, охватывающую только q0 и σ1, но не σ2
Тогда ваша поверхность находится в толще проводника. Естественно, поток вектора напряжённости через неё равен нулю.

#51254 iliaborisov :ВЕДЬ если бы мы рассматривали бы ситуацию с внешним посторонним зарядом вне шара, то Вас бы не удивило бы то, что в таком случае сторонний заряд ТАК влияет на распределение внешнего заряда на поверхности металла, что он распределен не равномерно. ХОТЯ внутри этого проводника поле ВСЕ равно остается равным нулю. А вот когда речь заходит о внутренних зарядах — то они почему то не влияют на распределение. Вот это то и непонятно
Внешний заряд влияет на распределение заряда на внешней поверхности шара и не влияет на распределение заряда на границе «шар-полость». Заряд в полости влияет на распределение заряда на границе «шар-полость» и не влияет на распределение заряда на поверхности шара. Всё логично. Поверхность металла — это и есть клетка Фарадея, которая маскирует всё, что находится по другую сторону от неё (за исключением величины заряда, если заряд внутри).
Поэтому изнутри клетки нельзя вести радиопередачу. Поэтому подводная лодка для ведения (да и для приёма) радиопередачи должна высунуть антенну над поверхностью моря.

#51258 givigudze :Хотя могу выдвинуть такую гипотезу. Что поле именно на поверхности сферы равно нулю, но как только мы чуток внутрь — так оно сразу начинает расти. И нашим бедным электронам некуда дется от этого сильного поля, остается только выстроится на поверхности сферы.
В точности наоборот. На поверхности сферы напряжённость поля есть, а чуток внутрь — и сразу ноль. И электроны никакого поля не чувствуют, с покойненько участвуют только в хаотическом тепловом движении.
Но дело в том что сами электроны же образуют поле, поэтому там где есть заряды не может быть нулевое поле.
Там и отрицательные электроны, и положительные ионы, в одинаковой концентрации. Напряжённость их суммарного поля ноль.
Но теорема Гаусса не оперирует электронами.
Для теоремы Гаусса абсолютно безразлично, что является носителем электрического заряда.
Вот кто из Вас расскажет как распределенно статическое электрическое поле в тоще металла.
Вроде бы всё уже рассказано.
С каким коэффициентом оно уменьшается, оно же не может оставаться таким же как и было.
Рассматривается статика. Вот перемещались заряды, была динамика, поле изменялось. А потов всё остановилось, и больше уже не изменяется.
Вот если мы в толщу диэлектрика между обкладками конденсатора просунем тонкую металлическую пластинку — то емкость уменьшится. Какая минимальная тощина металла в сфере должна быть что бы заряд по внешней поверхности распространялся равномерно при наличии внутри заряда в какой-то точке.
2-3 шага кристаллической решётки.
А ну сделали мы сферу из графита и ?
И всё точно так же. Графит — хороший проводник.
Металлическая сфера обладает сверхпроводимостью.
Обычно нет. Но может быть и сверхпроводящая. Тогда она ещё и магнитное поле будет выталкивать.

Тогда ваша поверхность находится в толще проводника. Естественно, поток вектора напряжённости через неё равен нулю.
Да, я ее и имел ввиду

#51431 zam :#51254 iliaborisov :ВЕДЬ если бы мы рассматривали бы ситуацию с внешним посторонним зарядом вне шара, то Вас бы не удивило бы то, что в таком случае сторонний заряд ТАК влияет на распределение внешнего заряда на поверхности металла, что он распределен не равномерно. ХОТЯ внутри этого проводника поле ВСЕ равно остается равным нулю. А вот когда речь заходит о внутренних зарядах — то они почему то не влияют на распределение. Вот это то и непонятно
Заряд в полости влияет на распределение заряда на границе «шар-полость» и не влияет на распределение заряда на поверхности шара.
А как это строго показать\доказать? То есть как доказать, что заряд внутри полости вкупе со слоем заряда (индуцированного) на поверхности полости дают суммарно напряженность ноль в толще шара (вне зависимости от того, какой заряд на внешней поврехности шара и как он распределен там ) в том числе когда эта полость находится не в центре шара? Когда в центре — там в общем действительно все ясно, исходя из симметрии — слои заряда соответственно тоже распределены равномерно, что дает равномерное поле с напряженностью ноль, точнее отдельно внешний слой заряда дает ноль внутри себя, т.к. равномерно распределен, а также слой заряда на поврехности полости — тоже оптому что равномерен — вкупе с точечным в центре центрированной полости дает ноль.

#51446 iliaborisov :А как это строго показать\доказать? То есть как доказать, что заряд внутри полости вкупе со слоем заряда (индуцированного) на поверхности полости дают суммарно напряженность ноль в толще шара в том числе когда эта полость находится не в центре шара?
Напряжённость поля внутри проводника равна нулю по той причине, что если бы было не так, то был бы электрический ток. Закон Ома: \({\displaystyle \mathbf {J} =\sigma \mathbf {E} }\), словами: (вектор плотности электрического тока) = (удельная проводимость)*(вектор напряжённости электрического поля). А у нас статика, никаких токов нет \(\displaystyle \mathbf {J} =0 \implies \mathbf {E}=0\).
Значит поток вектора напряжённости по любой оболочке, проходящей по телу проводника, равен нулю.
Значит, сумма зарядов внутри оболочки равна нулю (теорема Гаусса).
Значит, величина центрального заряда равна заряду на границе «металл-полость» (с противоположным знаком).

Есть ли формула (закон) о расспространении (распределении) электростатического поля внутри металла (в толще металла)?
Для переменного поля есть понятие скин-слоя, формулы и прочее. Никакой экран полностью не экранирует переменное электромагнитное поле. Просто когда волна проходит толщину скин-слоя она уменьшается в 2,7 раза.
Да, действительно если в проводнике (в металле) появится электрическое поле то и появится электрический ток. Но поле от разности потенцилов от одного конца провода до другого — это одно, а просто один заряд, от которого мы условно рисует силовые линии — это другое. Ток будет в металле когда есть разность потенциалов.
Опять же когда у нас есть длинный провод и разность потенциалов на концах — именно электрическое поле распространчется в металле и запускает электрический ток (постоянный). Да переменный ток течет в границе раздела сред между проводом и изолятором или между проводом и воздухом. Но у нас то постоянный ток.
И тогда вполне резонный вопрос. Мы взяли сферу из реального металла — там из алюминия, поместили внутрь заряд, она зарядилась и все стало как на картинке. Будет ли это состоягие сохраняться значительно долго (ну хотя бы секунд 5) или же тут же побегут токи в сфере и весь заряд уйдет на нагрев током металла?
Почему бы одному заряду из внешнего слоя не пробратся внутрь сферы к противоположному ? Какая сила его держит на поврехности сферы ? В диоде — там понятно потенциальный барьер.
Что-то я припоминаю что электрическое поле распространяется по поверхности метала, а перпендикулярно вглубь — нет. Но где формула, где закон, где прочитать ?

#51448 zam :#51446 iliaborisov :А как это строго показать\доказать? То есть как доказать, что заряд внутри полости вкупе со слоем заряда (индуцированного) на поверхности полости дают суммарно напряженность ноль в толще шара в том числе когда эта полость находится не в центре шара?
Напряжённость поля внутри проводника равна нулю по той причине, что если бы было не так, то был бы электрический ток. Закон Ома: \({\displaystyle \mathbf {J} =\sigma \mathbf {E} }\), словами: (вектор плотности электрического тока) = (удельная проводимость)*(вектор напряжённости электрического поля). А у нас статика, никаких токов нет \(\displaystyle \mathbf {J} =0 \implies \mathbf {E}=0\).
Значит поток вектора напряжённости по любой оболочке, проходящей по телу проводника, равен нулю.
Значит, сумма зарядов внутри оболочки равна нулю (теорема Гаусса).
Значит, величина центрального заряда равна заряду на границе «металл-полость» (с противоположным знаком).
«А у нас статика, никаких токов нет \(\displaystyle \mathbf {J} =0 \implies \mathbf {E}=0\).» Да, только напряженность поля, равное нулю создается суперпозицией полей от ТРЕХ зарядов, в том числе и на внешней поверхности. А нам надо доказать, что оно равно нулю УЖЕ от двух — от центрального +на границе полости. Третье уже да, тогда автоматом идет равное нулю.

#51452 givigudze :Есть ли формула (закон) о расспространении (распределении) электростатического поля внутри металла (в толще металла)?
Написано выше.
Для переменного поля есть понятие скин-слоя, формулы и прочее. Никакой экран полностью не экранирует переменное электромагнитное поле. Просто когда волна проходит толщину скин-слоя она уменьшается в 2,7 раза.
Да. Говорят, можно позвонить на мобильник, лежащий в кастрюле. Только мне кажется, это из-за неплотно лежащей крышки. Во всяком случае, когда я захожу в лифт и двери закрываются, связь прерывается.
Да, действительно если в проводнике (в металле) появится электрическое поле то и появится электрический ток.
Появится поле с ненулевой напряжённостью. Да.
Но поле от разности потенцилов от одного конца провода до другого — это одно, а просто один заряд, от которого мы условно рисует силовые линии — это другое.
Поле не бывает от разности потенциалов. Электрическое поле бывает от электрических зарядов (1) и от переменного магнитного поля (2). А потенциал — универсальная характеристика электрического поля для случая (1). Для случая (2) понятия электрического потенциала нет (поле вихревое).
Ток будет в металле когда есть разность потенциалов.
Да.
Опять же когда у нас есть длинный провод и разность потенциалов на концах — именно электрическое поле распространчется в металле и запускает электрический ток (постоянный). Да переменный ток течет в границе раздела сред между проводом и изолятором или между проводом и воздухом.
Переменный ток течёт и через изолятор, и через воздух - в общем, через конденсатор. Он в этом случае называется током смещения.
Но у нас то постоянный ток.
Где? Я считал, что у нас тока нет, статика.
И тогда вполне резонный вопрос. Мы взяли сферу из реального металла — там из алюминия, поместили внутрь заряд, она зарядилась и все стало как на картинке. Будет ли это состоягие сохраняться значительно долго (ну хотя бы секунд 5) или же тут же побегут токи в сфере и весь заряд уйдет на нагрев током металла? сос
Это состояние будет сохраняться вечно.
Почему бы одному заряду из внешнего слоя не пробратся внутрь сферы к противоположному ? Какая сила его держит на поврехности сферы ? В диоде — там понятно потенциальный барьер.
Электростатическая сила отталкивания от соседей. Равнодействующая таких сил направлена от центра сферы. Вопрос — почему же он не улетает? А вот тут как раз потенциальный барьер на поверхности металла. Чтобы его преодолеть, необходимо электрону придать дополнительную энергию (работа выхода)..
Что-то я припоминаю что электрическое поле распространяется по поверхности метала, а перпендикулярно вглубь — нет. Но где формула, где закон, где прочитать ?
Пожалуй там, с чего начали - теорема о единственности решения электростатической задачи. Ссылка в сообщении 51124

Да. Говорят, можно позвонить на мобильник, лежащий в кастрюле. Только мне кажется, это из-за неплотно лежащей крышки. Во всяком случае, когда я захожу в лифт и двери закрываются, связь прерывается.
ВЫскажу предполложение — так как тут электрическое поле переменное, то электроны, которые перестраиваясь в куске металла под воздействием внешнего поля своим полем противодействуют внешнему — изза скорости изменения вектора напряженности — не успевают должным образом переместиться и таким образом лишь частично гасят внешнее поле. Плюс уже забыл — каак там ведет себя магнитное поле по отношению к металлу — гасится или нет.

Магнитное поле как переменное так и постоянное проходит сквозь металл с определенной зависимостью, описывется это уравнениями Максвелла.
Теорема об единственности решения — это об распределении заряда по сфере и о том что поле внутри равно нулю. Но не ораспределении электрического поля в толще металла. Доказательство теоремы — слабое. Если то не то — то это не это, а то то нето то не туда, а сюда. Сильное доказательство будет опираться на уравнения Максвелла.

#51481 iliaborisov :каак там ведет себя магнитное поле по отношению к металлу — гасится или нет.
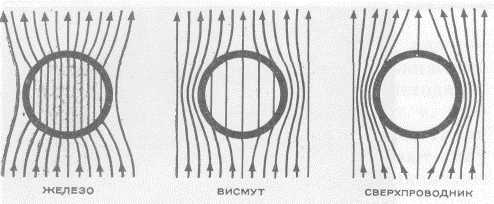
Тут слева ферромагнетик, в центре парамагнетик, справа сверхпроводник (идеальныйдиамагнетик).

Это про постоянные магнитные поля ? А есть ли доказательства про сверхпроводник ? Какая сила будет выталкивать магнитное поле из сферы из сверхпроводника ?
Магнитное поле действует только на движущиеся заряды. Так же только движущиеся заряды создают магнитное поле.
В феррамагнитеках там есть магнитные диполи соединенные в домены. Какие структуры образуются в сверхпроводящей сфере ?
Когда в школе рассказывали про диамагнетики и парамагнетики — было все понятно. Но после изучения уравнений Максвелла и технической электродинамики появились серьезные сомнения.
Феррамагнетики — структурируются по полю и как бы втягивают поле в себя. Условно говоря усиливают его в себе и немного разряжают вокруг.
Диамагенетики — структурируются приемущественно против поля (не знаю почему и как) и гасят поле внутри себя за счет усиления вокруг себя.
А вот что со сверхпроводником ? По сопротивлению висмут от железа то не особо отличаются. Хотя вот есть медь — диамагнетик, хороший проводник.
Создаются ли в сверхпроводнике магнитные диполи ?
Впринципе то все верно. Но есть ли объяснения образования магнитных диполей в сверхпроводнике ?

#51562 givigudze :Это про постоянные магнитные поля ? А есть ли доказательства про сверхпроводник ?
Какие доказаельства? Это наблюдаемый эффект.

Магнит висит над чашкой из сверхпроводящего матерала. И будет так висеть вечно, пока поддерживается сверхпроводимость.
Какая сила будет выталкивать магнитное поле из сферы из сверхпроводника ?
Это так условно говорится — выталкивает. На самом деле внешнее магнитное поле полностью компенсируется полем внутренним, созданным электрическими токами внутри сверхпроводника. Ведь электронам (точнее, куперовскм парам) ничто не мешает двигаться — сверхпроводнк, сопротивление ноль.
Магнитное поле действует только на движущиеся заряды. Так же только движущиеся заряды создают магнитное поле.
Ещё магнитные диполи создают магнитное поле.
В феррамагнитеках там есть магнитные диполи соединенные в домены. Какие структуры образуются в сверхпроводящей сфере ?
Никакие не образуются.
Создаются ли в сверхпроводнике магнитные диполи ?
Нет.
Кстати. Ферромагнетизм (как и сверхпроводимость) на может быть объяснён в рамках классической физики. Только квантовая.




