Помогите решить задачу

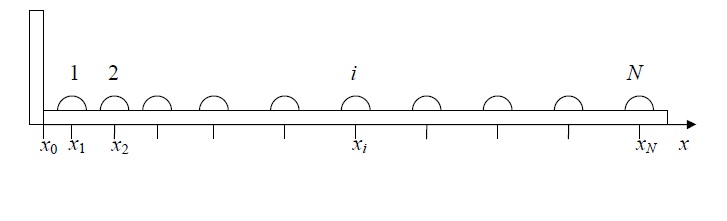
На длинном гладком прямом горизонтальном жёлобе расположено чётное число N одинаковых

маленьких гладких шариков. С левой стороны жёлоб ограничен вертикальной стенкой (см. рис.).

Ось х направлена вправо от стенки так, что координата стенки х0, а координата i-го шарика (1 ≤ i ≤

N) равна xi. При этом выполняются соотношения: x1-х0=a/2 и, для i>1, xi - xi-1 = a, где a = 1 вершок. В

начальный момент времени все шарики одновременно начинают двигаться с одной и той же по

модулю скоростью v, причём шарики с нечётными номерами – вправо, а с чётными – влево. Через

время t = 100 с после начала движения первый шарик оказался в первоначальном положении

последнего (в точке с координатой xN). Найдите скорость v. Столкновения шариков между собой и

со стенкой считайте абсолютно упругими; размерами шариков по сравнению с величиной a

пренебрегите. Справка: вершок – старинная русская единица длины; составляет 4,445 см.

Система

x1-х0=4,445/2

xi - xi-1 = 4.445