2 закон Ньютона

Тело массой m вращается в вертикальной плоскости на жесткой невесомой штанге.Найти разность сил натяжения штанги в двух случаях
1)скорость вращения постоянна
2)скорость вращения не постоянна ,а вызвана силой тяжести

Вот Вам силы и помня, что центростремительное ускорение всегда направлено к центру напишите уравнение динамики для двух положений и всё решится для постоянной скорости. Для второго случая надо использовать закон сохранения энергии. Предложите Ваши мысли.


C 1 случаем я решил
1)aцm=mg+T2
-ацm=mg-T1
T1-T2=2mg
С б) проблема была, но сейчас попробую с помощью сохранения энергии решить
Благодарю за подсказку
Добавлено спустя 42 минут
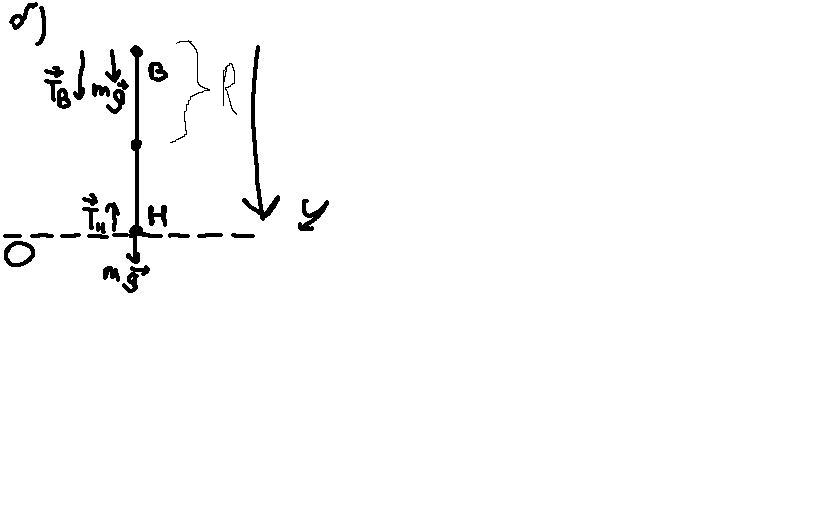
Как я понимаю во втором случае ац будет зависит от g. В точке В ускорение равно ац=u^2/r ,но u=0 потому что тело начинает двиг из положения равновесия из этого следует
1)0=mg+T(в)
По ЗСМЭ в точке Н (рассматриваем движение относительно оси 0)
2)Е до=Е после
2Rmg=U^2/2 из этого следует, что U^2=4Rg
По 2 закону Ньютона
На точку Н действуют
3)-ацm=mg-T(н)
подставив в (3) (2) получим
4)T(н)=5mg
5)T(в)= -mg
6)T(н)-T(в)=6mg
ПРАВИЛЬНО?
отредактировал(а) grisha2207: 2012-11-10 16:51 GMT

Всё верно. У меня бы были такие студенты! Удачи.




