Распространение механической волны, представляющее собой последовательную передачу движения от одного участка среды к другому, означает тем самым передачу энергии. Эту энергию доставляет источник волны, когда он приводит в движение непосредственно прилегающий к нему слой среды. От этого слоя энергия передается следующему слою и т. д. Таким образом, распространение волны создает в среде ноток энергии, расходящийся от источника. Представление о потоке энергии, переносимой волнами, впервые ввел в 1874г. русский физик Николай Алексеевич Умов (1840—1915), Он получил и формулу, позволяющую вычислить интенсивность волны.
При встрече волны с различного рода телами переносимая ею энергия может произвести работу или превратиться в другие виды энергии.
Яркий пример такого переноса энергии без переноса вещества дают нам взрывные волны. На расстояниях во много десятков метров от места разрыва бомбы, куда недолетают ни осколки, ни поток горячего воздуха, взрывная волна выбивает стекла, ломает стены и т. п., т. е. производит большую механическую работу. Но энергия переносится, конечно, и самыми слабыми волнами; например, летящий комар излучает звуковую волну («комариный писк»), мощность которой, т. е. энергия, излучаемая в
![]() , составляет около
, составляет около
![]() .
.
Если размеры источника достаточно малы и энергия от него распространяется во все стороны равномерно, то источник можно рассматривать как точенный, а расходящаяся от него волна будет сферической. В этом случае энергия, изучаемая источником, равномерно распределяется по всей поверхности волновой сферы. Нетрудно видеть, что энергия, приходящаяся на единицу поверхности этой сферы, будет тем меньше, чем больше радиус сферы. Площадь сферы или любого вырезанного в ней конусом участка (рис. 80) растет пропорционально квадрату радиуса, т. е. при увеличении расстояния от источника вдвое площадь увеличивается вчетверо, и на каждую единицу поверхности сферы приходится вчетверо меньшая энергия волны.
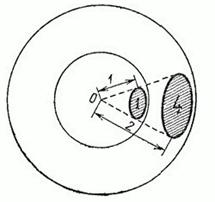
Рис. 80. При увеличении радиуса вдвое площадь поверхности возрастает вчетверо
Энергию, переносимую волной через сечение, площадь которого равна
![]() , за время, равное
, за время, равное
![]() , т. е. мощность, переносимую через единичное сечение, называют интенсивностью волны. Таким образом, интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника.
, т. е. мощность, переносимую через единичное сечение, называют интенсивностью волны. Таким образом, интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника.
Указанная выше мощность звука летящего комара на расстоянии
![]() от него распределяется по сферической поверхности, площадь которой равна
от него распределяется по сферической поверхности, площадь которой равна
![]() , т. е. интенсивность звука составляет на таком расстоянии около
, т. е. интенсивность звука составляет на таком расстоянии около
![]() Эта ничтожная величина близка к порогу слышимости и дает представление о чрезвычайно высоком чувствительности нашего уха.
Эта ничтожная величина близка к порогу слышимости и дает представление о чрезвычайно высоком чувствительности нашего уха.
Если ограничить возможность расхождения волны в стороны, то и убывание интенсивности уменьшится. Так, например, звуковая волна, распространяющаяся в трубе, не расходится в стороны и поэтому на длинном пути сохраняет большую интенсивность. На этом основано применение переговорных труб, которые и теперь еще зачастую можно видеть на небольших кораблях, где они служат для связи капитанского мостика с машинным отделением, с кабиной рулевого и т. п. (рис. 81).
Для увеличения громкости звука на больших расстояниях иногда применяются рупоры (рис. 82). Следует, однако, иметь в виду, что вне рупора расхождение волны в стороны уже не ограничено и причина усиления звука здесь иная: рупор концентрирует энергию волны в некотором телесном угле, т. е. создает направленное излучение (§ 42). Но внутри этого телесного угла интенсивность убывает обратно пропорционально квадрату расстояния. Интенсивность волны, распространяющейся в цилиндрической трубе, не должна была бы уменьшаться с расстоянием, так как энергия переносится здесь через сечения одинаковой площади. Однако в действительности происходит ослабление, вызванное поглощением энергии волны той средой, в которой она распространяется. В каждой точке на пути волны часть переносимой ею энергии тратится на работу против сил трения (вязкости) в среде и переходит в тепло. Благодаря поглощению интенсивность сферической волны убывает фактически еще быстрее, чем обратно пропорционально квадрату расстояния. При распространении в трубе энергия волны поглощается, кроме того, и стенками самой трубы.
Рис. 81. Переговорная труба на корабле
Рис. 82. Рупор (мегафон) дает направленное излучение
Электромагнитные волны представляют собой передачу изменений электромагнитного поля. Они, конечно, тоже переносят энергию, но не в форме кинетической и потенциальной энергии частиц среды, а в виде энергии электрического и магнитного полей. Именно в таком виде поступает от Солнца вся энергия, за счет которой поддерживается жизнь на Земле. Общая мощность электромагнитных волн, излучаемых Солнцем, выражается числом
![]() . На расстоянии 150 миллионов километров, т. е. на таком удалении от Солнца, на котором находится Земля, интенсивность электромагнитных волн равна
. На расстоянии 150 миллионов километров, т. е. на таком удалении от Солнца, на котором находится Земля, интенсивность электромагнитных волн равна
![]() . Эта последняя величина называется солнечной постоянной. Из-за отражения от облаков, рассеяния и поглощения в атмосфере до земной поверхности доходит примерно
. Эта последняя величина называется солнечной постоянной. Из-за отражения от облаков, рассеяния и поглощения в атмосфере до земной поверхности доходит примерно
![]() этой энергии (см. том I, §308).
этой энергии (см. том I, §308).
Если бы Солнце удалилось от нас на расстояние ближайшей звезды, т. е. на 4 световых года, то интенсивность его электромагнитного излучения у Земли составила бы всего
![]() . И все же, если бы даже лишь сотая часть этой энергии приходилась на видимый свет, то и тогда интенсивность последнего во много раз превосходила бы порог чувствительности нашего глаза.
. И все же, если бы даже лишь сотая часть этой энергии приходилась на видимый свет, то и тогда интенсивность последнего во много раз превосходила бы порог чувствительности нашего глаза.
Интересно отметить, что порог чувствительности глаза примерно такой же, как и уха. Глаз способен реагировать на потоки световой энергии около
![]() . Впрочем, современные радиоприемники могут соперничать по чувствительности с глазом: хороший приемник может «услышать» радиостанцию, волны которой имеют в месте приема интенсивность
. Впрочем, современные радиоприемники могут соперничать по чувствительности с глазом: хороший приемник может «услышать» радиостанцию, волны которой имеют в месте приема интенсивность
![]() .
.












Комментарии: (0)