Изучение видимого движения планет на неизменном фоне звездного неба позволило дать полное кинематическое описание движения планет относительно инерциальной системы отсчета Солнце — звезды. Траектории планет оказались замкнутыми кривыми, получившими название орбит. Орбиты близки к окружностям с центром в Солнце, а движение планет по орбитам оказалось близким к равномерному. Исключение составляют только кометы и некоторые астероиды, расстояние от которых до Солнца и скорость движения которых меняются в широких пределах, а орбиты сильно вытянуты. Расстояния от планет до Солнца (радиусы орбит) и времена обращения этих планет вокруг Солнца весьма различны (табл. 2). Обозначения первых шести планет, приведенные в таблице, сохранились еще со времен астрологов.
Таблица 2. Сведения о планетах
Название и обозначение планеты | Расстояние от Солнца | Время обращения в земных годах | |
В радиусах земной орбиты | В млн. км | ||
Меркурий Венера Земля Марс Юпитер Сатурн Уран Нептун Плутон | 0,387 0,723 1,000 1,524 5,203 9,938 19,191 30,071 39,6 | 58 108 149 228 778 1426 2868 4494 6000 | 0,241 0,615 1,000 1,881 11,862 29,457 84,013 164,783 248 |
В действительности орбиты планет не вполне круговые, а их скорости не вполне постоянны. Точное описание движений всех планет было дано немецким астрономом Иоганном Кеплером (1571—1630) — в его время были известны только первые шесть планет — в виде трех законов (рис. 199).
1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.
2. Радиус-вектор планеты (вектор, проведенный от Солнца к планете) в равные времена описывает равные площади.
3. Квадраты времен обращения любых двух планет относятся как кубы больших полуосей их орбит.
Из этих законов можно сделать ряд выводов о силах, под действием которых движутся планеты. Рассмотрим вначале движение какой-либо одной планеты. Ближайший к Солнцу ( ![]() ) конец
) конец ![]()
![]() большой оси орбиты называют перигелием; другой конец
большой оси орбиты называют перигелием; другой конец ![]() называют афелием (рис. 200). Так как эллипс симметричен относительно обеих своих осей, то радиусы кривизны в перигелии и афелии равны. Значит, согласно сказанному в § 27, нормальные ускорения
называют афелием (рис. 200). Так как эллипс симметричен относительно обеих своих осей, то радиусы кривизны в перигелии и афелии равны. Значит, согласно сказанному в § 27, нормальные ускорения ![]() и
и ![]() в этих точках относятся как квадраты скоростей планеты
в этих точках относятся как квадраты скоростей планеты ![]() и
и ![]() :
:
![]() (123.1)
(123.1)
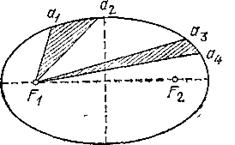
Рис. 199. Если из точки ![]() в точку
в точку ![]() планета перемещается за то же время, что из точки
планета перемещается за то же время, что из точки ![]() в точку
в точку ![]() , то площади, заштрихованные на рисунке, равны
, то площади, заштрихованные на рисунке, равны
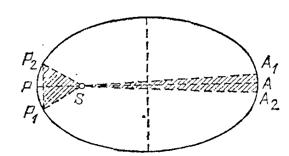
Рис. 200. К определению отношения скоростей планеты в перигелии и афелии
Рассмотрим малые пути ![]() и
и ![]() , симметричные относительно перигелия и афелия и совершаемые за одинаковые промежутки времени
, симметричные относительно перигелия и афелия и совершаемые за одинаковые промежутки времени ![]() . Согласно второму закону Кеплера площади секторов
. Согласно второму закону Кеплера площади секторов ![]() и
и ![]() должны быть равны. Дуги эллипса
должны быть равны. Дуги эллипса ![]() и
и ![]() равны
равны ![]() и
и ![]() . На рис.200 для наглядности дуги сделаны довольно большими. Если же взять эти дуги крайне малыми (для чего промежуток времени
. На рис.200 для наглядности дуги сделаны довольно большими. Если же взять эти дуги крайне малыми (для чего промежуток времени ![]() должен быть малым), то отличием дуги от хорды можно пренебречь и рассматривать описанные радиус-вектором секторы как равнобедренные треугольники
должен быть малым), то отличием дуги от хорды можно пренебречь и рассматривать описанные радиус-вектором секторы как равнобедренные треугольники ![]() и
и ![]() . Их площади равны соответственно
. Их площади равны соответственно ![]() и
и ![]() , где
, где ![]() и
и ![]() — расстояния от афелия и перигелия до Солнца. Значит,
— расстояния от афелия и перигелия до Солнца. Значит, ![]() , откуда
, откуда ![]() . Наконец, подставляя это соотношение в (123.1), найдем
. Наконец, подставляя это соотношение в (123.1), найдем
![]() . (123.2)
. (123.2)
Так как в перигелии и афелии тангенциальные ускорения равны нулю, то ![]() и
и ![]() представляют собой ускорения планеты в этих точках. Они направлены к Солнцу (вдоль большой оси орбиты).
представляют собой ускорения планеты в этих точках. Они направлены к Солнцу (вдоль большой оси орбиты).
Расчет показывает, что и во всех других точках траектории ускорение направлено к Солнцу и изменяется по тому же закону, т. е. обратно пропорционально квадрату расстояния планеты от Солнца; поэтому для любой точки орбиты
![]() , (123.3)
, (123.3)
где ![]() — ускорение планеты,
— ускорение планеты, ![]() — расстояние от нее до Солнца. Таким образом, ускорение планеты обратно пропорционально квадрату расстояния между Солнцем и планетой. Рассматривая угол, составляемый радиус-вектором планеты с касательной к траектории, видим (рис. 201), что при движении планеты от афелия к перигелию тангенциальная составляющая ускорения
— расстояние от нее до Солнца. Таким образом, ускорение планеты обратно пропорционально квадрату расстояния между Солнцем и планетой. Рассматривая угол, составляемый радиус-вектором планеты с касательной к траектории, видим (рис. 201), что при движении планеты от афелия к перигелию тангенциальная составляющая ускорения ![]() положительная скорость планеты растет; наоборот, при движении от перигелия к афелию скорость планеты уменьшается. В перигелии планета достигает наибольшей скорости, в афелии — наименьшей скорости движения.
положительная скорость планеты растет; наоборот, при движении от перигелия к афелию скорость планеты уменьшается. В перигелии планета достигает наибольшей скорости, в афелии — наименьшей скорости движения.
Для выяснения зависимости ускорения планеты от расстояния ее до Солнца мы воспользовались первыми двумя законами Кеплера. Эту зависимость удалось найти потому, что планеты движутся по эллипсам, изменяя свое расстояние от Солнца. Если бы планеты двигались по окружностям, расстояние от планеты до Солнца и ее ускорение не менялись бы, и мы не смогли бы найти эту зависимость.
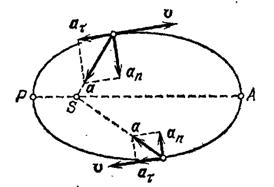
Рис. 201. При движении планеты от перигелия к афелию сила притяжения уменьшает скорость планеты, при движении от афелия к перигелию – увеличивает скорость планеты
Но при сравнении между собой ускорений различных планет можно удовлетвориться приближенным описанием движения планет, считая, что они движутся равномерно по окружностям. Обозначим радиусы орбит двух каких-нибудь планет через ![]() и
и ![]() , а периоды их обращения — через
, а периоды их обращения — через ![]() и
и ![]() . Тогда их скорости выразятся формулами
. Тогда их скорости выразятся формулами
![]() ,
,
а центростремительные ускорения, согласно (27.1),— формулами.
![]() .
.
Так как движение по окружности мы считаем равномерным, то ![]() и
и ![]() можно считать ускорениями, направленными к центру орбиты — к Солнцу. Отношение ускорений планет
можно считать ускорениями, направленными к центру орбиты — к Солнцу. Отношение ускорений планет
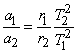 . (123.4)
. (123.4)
Но, согласно третьему закону Кеплера,
![]() .
.
Подставляя отношение квадратов времен обращения в формулу (123.4), найдем
![]() .
.
Этот вывод можно переписать в таком виде: для любой планеты, находящейся на расстоянии ![]() от Солнца, ее ускорение
от Солнца, ее ускорение
![]() (123.5)
(123.5)
где ![]() — одна и та же постоянная для всех планет солнечной системы. Таким образом, ускорения планет обратно пропорциональны квадратам их расстояний от Солнца и направлены к Солнцу.
— одна и та же постоянная для всех планет солнечной системы. Таким образом, ускорения планет обратно пропорциональны квадратам их расстояний от Солнца и направлены к Солнцу.

 (или
(или  )
)
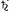

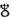
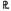












Комментарии: (0)