Средняя скорость. В § 9 мы говорили, что утверждение о равномерности данного движения справедливо только с той степенью точности, с которой произведены измерения. Например, применив секундомер, можно обнаружить, что движение поезда, представлявшееся при грубом измерении равномерным, оказывается неравномерным при более тонком измерении.
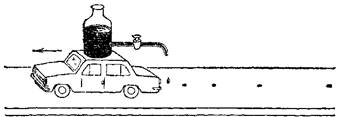
Но когда поезд подходит к станции, мы обнаружим неравномерность его движения даже без секундомера. Даже грубые измерения покажут нам, что промежутки времени, за которые поезд проходит расстояния от одного телеграфного столба до другого, становятся все больше и больше. С той малой степенью точности, которую дает измерение времени по часам, движение поезда на перегоне равномерно, а при подходе к станции — неравномерно. Поместим на игрушечный заводной автомобиль капельницу, заведем его и пустим катиться по столу. В середине движения расстояния между каплями оказываются одинаковыми (движение равномерно), но затем, когда завод приблизится к концу, будет заметно, что капли ложатся все ближе одна к другой — движение неравномерно (рис. 25).
|
| Рис. 25. Следы капель, равномерно падающих из капельницы, помещенной на движущийся заводной автомобиль, перед окончанием завода |
При неравномерном движении нельзя говорить о какой-то определенной скорости, так как отношение пройденного пути к соответственному промежутку времени не одинаково для разных участков, как это имело место для равномерного движения. Если, однако, нас интересует движение только на каком-либо определенном участке пути, то это движение в целом можно охарактеризовать, введя понятие средней скорости движения:средней скоростью неравномерного движения на данном участке пути называют отношение длины этого участка к промежутку времени, за который этот участок пройден:
|
|
Отсюда видно, что средняя скорость равна скорости такого равномерного движения, при котором тело прошло бы данный участок пути за тот же промежуток времени, что и при действительном движении.
Как и в случае равномерного движения, можно пользоваться формулой
![]() для определения пути, пройденного за данный промежуток времени при определенной средней скорости, и формулой
для определения пути, пройденного за данный промежуток времени при определенной средней скорости, и формулой
![]() для определения времени, за которое пройден данный путь с данной средней скоростью. Но пользоваться этими формулами можно только для того участка пути и для того промежутка времени, для которых эта средняя скорость была рассчитана. Например, зная среднюю скорость на участке пути АВ и зная длину АВ, можно определить время, за которое был пройден этот участок, но нельзя найти время, за которое была пройдена половина участка АВ, так как средняя скорость на половине участка при неравномерном движении, вообще говоря, не будет равна средней скорости на всем участке.
для определения времени, за которое пройден данный путь с данной средней скоростью. Но пользоваться этими формулами можно только для того участка пути и для того промежутка времени, для которых эта средняя скорость была рассчитана. Например, зная среднюю скорость на участке пути АВ и зная длину АВ, можно определить время, за которое был пройден этот участок, но нельзя найти время, за которое была пройдена половина участка АВ, так как средняя скорость на половине участка при неравномерном движении, вообще говоря, не будет равна средней скорости на всем участке.
Если для любых участков пути средняя скорость оказалась одинаковой, то это значит, что движение равномерное и средняя скорость равна скорости этого равномерного движения.
Если средняя скорость известна за отдельные последовательные промежутки времени, то можно найти среднюю скорость и за суммарное время движения. Пусть, например, поезд двигался в течение двух часов, причем его средняя скорость за первые 10 мин равнялась 18 км/ч, за следующие полтора часа — 50 км/ч и за остальное время — 30 км/ч. Найдем пути, пройденные за отдельные промежутки времени. Они будут равны
![]() км;
км;
![]() км;
км;
![]() км. Значит, общий путь, пройденный поездом, есть
км. Значит, общий путь, пройденный поездом, есть
![]() км. Поскольку весь этот путь был пройден за два часа, искомая средняя скорость
км. Поскольку весь этот путь был пройден за два часа, искомая средняя скорость
![]() км/ч.
км/ч.
Из этого примера видно, как вычислять среднюю скорость и в общем случае, когда известны средние скорости движения
![]() с которыми тело двигалось в течение последовательных промежутков времени
с которыми тело двигалось в течение последовательных промежутков времени
![]() . Средняя скорость всего движения выразится формулой
. Средняя скорость всего движения выразится формулой
|
|
Важно отметить, что в общем случае средняя скорость не равна среднему значению от средних скоростей на отдельных участках пути.
14.1. Покажите, что средняя скорость на всем пути будет больше наименьшей из средних скоростей на отдельных участках и меньше наибольшей из них.
14.2. Поезд проходит первые 10 км со средней скоростью 30 км/ч, вторые 10 км — со средней скоростью 40 км/ч, третьи 10 км — со средней скоростью 60 км/ч. Какова была средняя скорость поезда на всем 30-ти километровом отрезке пути?













Комментарии: (0)