Если траектория движения точки известна, то зависимость пути
![]() , пройденного точкой, от истекшего промежутка времени
, пройденного точкой, от истекшего промежутка времени
![]() дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.2). Связь между
дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.2). Связь между
![]() и
и
![]() для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид
для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид
![]() . Составим таблицу пути и времени такого движения:
. Составим таблицу пути и времени такого движения:
| t, с | 1 | 2 | 3 | 4 | 5 | 6 | … |
| s, м | 2 | 4 | 6 | 8 | 10 | 12 | … |
Зависимость одной величины от другой часто бывает удобно изображать не формулами или таблицами, а графиками, которые более наглядно показывают картину изменения переменных величин и могут облегчать расчеты. Построим график зависимости пройденного пути от времени для рассматриваемого движения. Для этого возьмем две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс) назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для изображения промежутков времени и пути и примем точку пересечения осей за начальный момент и за начальную точку на траектории. Нанесем на осях значения времени и пройденного пути для рассматриваемого движения (рис. 18). Для «привязки» значений пройденного пути к моментам времени проведем из соответственных точек на осях (например, точек 3 с и 6 м) перпендикуляры к осям. Точка пересечения перпендикуляров соответствует одновременно обеим величинам: пути
![]() и моменту
и моменту
![]() , — этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных путей, получая для каждой такой пары значений время — путь одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.
, — этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных путей, получая для каждой такой пары значений время — путь одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.
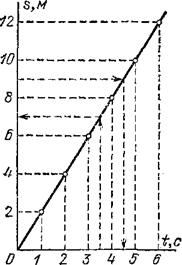
Рис. 18. График пути равномерного движения со скоростью 2 м/с
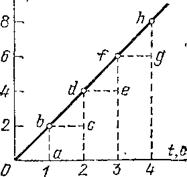
Рис. 19. К упражнению 12.1
В нашем случае график пути оказался прямой линией. Можно показать, что график пути равномерного движения всегда есть прямая линия; и обратно: если график зависимости пути от времени есть прямая линия, то движение равномерно.
Повторяя построение для другой скорости движения, найдем, что точки графика для большей скорости лежат выше, чем соответственные точки графика для меньшей скорости (рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.
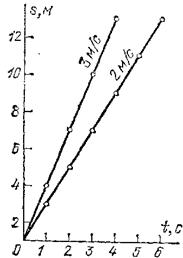
Рис. 20. Графики пути равномерных движений со скоростями 2 и 3 м/с
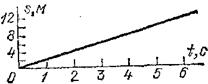
Рис. 21. График того же движения, что на рис. 18, вычерченный в другом масштабе
Наклон графика зависит, конечно, не только от числового значения скорости, но и от выбора масштабов времени и длины. Например, график, изображенный на рис. 21, дает зависимость пути от времени для того же движения, что и график рис. 18, хотя и имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков можно только в том случае, если они вычерчены в одном и том же масштабе.
С помощью графиков пути можно легко решать разные задачи о движении. Для примера на рис. 18 штриховыми линиями показаны построения, необходимые для того, чтобы решить следующие задачи для данного движения: а) найти путь, пройденный за время 3,5 с; б) найти время, за которое пройден путь 9 м. На рисунке графическим путем (штриховые линии) найдены ответы: а) 7 м; б) 4,5 с.
На графиках, описывающих равномерное прямолинейное движение, можно откладывать по оси ординат вместо пути
![]() координату
координату
![]() движущейся точки. Такое описание открывает большие возможности. В частности, оно позволяет различать направление движения по отношению к оси
движущейся точки. Такое описание открывает большие возможности. В частности, оно позволяет различать направление движения по отношению к оси
![]() . Кроме того, приняв начало отсчета времени за нуль, можно показать движение точки в более ранние моменты времени, которые следует считать отрицательными.
. Кроме того, приняв начало отсчета времени за нуль, можно показать движение точки в более ранние моменты времени, которые следует считать отрицательными.
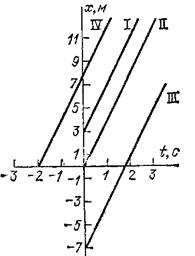
Рис. 22. Графики движений с одной и той же скоростью, но при различных начальных положениях движущейся точки
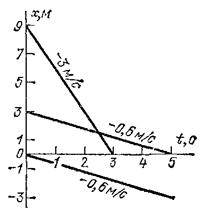
Рис. 23. Графики нескольких движений с отрицательными скоростями
Например, на рис. 22 прямая I есть график движения, происходящего с положительной скоростью 4 м/с (т. е. в направлении оси
![]() ), причем в начальный момент движущаяся точка находилась в точке с координатой
), причем в начальный момент движущаяся точка находилась в точке с координатой
![]() м. Для сравнения на том же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в точке с координатой
м. Для сравнения на том же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в точке с координатой
![]() (прямая II). Прямая. III соответствует случаю, когда в момент
(прямая II). Прямая. III соответствует случаю, когда в момент
![]() движущаяся точка находилась в точке с координатой
движущаяся точка находилась в точке с координатой
![]() м. Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела координату
м. Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела координату
![]() в момент
в момент
![]() с.
с.
Мы видим, что наклоны всех четырех графиков одинаковы: наклон зависит только от скорости движущейся точки, а не от ее начального положения. При изменении начального положения весь график просто переносится параллельно самому себе вдоль оси
![]() вверх или вниз на соответственное расстояние.
вверх или вниз на соответственное расстояние.
Графики движений, происходящих с отрицательными скоростями (т. е. в направлении, противоположном направлению оси
![]() ), показаны на рис. 23. Они представляют собой прямые, наклоненные вниз. Для таких движений координата
), показаны на рис. 23. Они представляют собой прямые, наклоненные вниз. Для таких движений координата
![]() точки с течением времени уменьшается.
точки с течением времени уменьшается.
12.3.
График пути для точки, движущейся со скоростью
![]() , отсекает на оси ординат отрезок
, отсекает на оси ординат отрезок
![]() . Как зависит от времени расстояние
. Как зависит от времени расстояние
![]() от начальной точки? Напишите формулу этой зависимости.
от начальной точки? Напишите формулу этой зависимости.
12.4.
Точка, движущаяся со скоростью
![]() , в момент
, в момент
![]() находится на расстоянии
находится на расстоянии
![]() от начальной. Как зависит от времени расстояние
от начальной. Как зависит от времени расстояние
![]() ?
?
12.5.
Точка, двигаясь равномерно вдоль оси
![]() , имела координаты
, имела координаты
![]() м и
м и
![]() м в моменты времени
м в моменты времени
![]() с и
с и
![]() с соответственно. Найдите графически, в какой момент точка проходила через начало координат и какова была координата
с соответственно. Найдите графически, в какой момент точка проходила через начало координат и какова была координата
![]() в начальный момент. Найдите проекцию скорости на ось
в начальный момент. Найдите проекцию скорости на ось
![]() .
.
12.6. Найдите при помощи графика пути, когда и на каком расстоянии от точки А автомашину, вышедшую из точки А, догонит вторая автомашина, вышедшая из той же точки через 20 мин после первой, если первая машина движется со скоростью 40 км/ч, а вторая — со скоростью 60 км/ч.
12.7. Найдите при помощи графика пути, где и когда встретятся автомашины, вышедшие одновременно навстречу друг другу со скоростями 40 и 60 км/ч из пунктов А и В, лежащих на расстоянии 100 км друг от друга.
Графики пути можно строить и для случаев, в которых тело движется равномерно в течение определенного промежутка времени, затем движется равномерно, но с другой скоростью в течение другого промежутка времени, затем снова меняет скорость и т. д. Например, на рис. 26 показан график движения, в котором тело двигалось в течение первого часа со скоростью 20 км/ч, в течение второго часа — со скоростью 40 км/ч и в течение третьего часа — со скоростью 15 км/ч.
12.8. Постройте график пути для движения, в котором за последовательные часовые промежутки тело имело скорости 10, -5, 0, 2, -7 км/ч. Чему равно суммарное перемещение тела?














Комментарии: (0)