Равнопеременное Прямолинейное Движение
Для этого случая, как и для предыдущего, достаточно выбрать одну из осей координат и направить ее вдоль траектории движения.
Положение материальной точки также будет описываться уравнением движения:
х = ft(t) или у = f2(t), или z = f3(t).
Равнопеременным движением называют такое движение, при котором ускорение есть величина постоянная ( а = const). Направление вектора ускорения при этом может совпадать с направлением начальной скорости движения или же быть направлено в противоположную сторону.
Если на каком-то отрезке времени скорость и ускорение совпадают по направлению, то движение называется равноускоренным, если же на данном отрезке времени эти векторные величины имеют противоположные направления - движение называется равнозамедленным.
Итак, при равнопеременном прямолинейном движении ускорение есть величина постоянная:
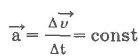
Отсюда следует:
Если отсчет времени вести от нуля, а начальную скорость соответственно обозначить v0, то можно записать:
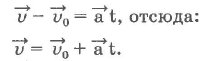
Соответственно в проекциях на ось Ох:
vx; v0 ; ax могут быть как положительными, так и отрицательными числами. Если знаки величин v0 и ах совпадают - движение равноускоренное, если они различны - движение равнозамедленное (при t, близких к нулю). Например, уравнения vx = 3 + 2t или vх = -1 - 3t - описывают равноускоренные движения.
Уравнения vх = 3 - 2t или vх = -2 + 3t при достаточно малых t показывают, что движения являются равнозамедленными.
Из уравнений ясно, что зависимость проекции скорости от времени является линейной, так как независимая переменная t входит в уравнение первой степени.
Чтобы вывести формулу зависимости координаты от времени для этого вида движения, обратимся к графику скорости.
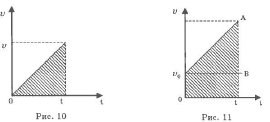
Для случая, при котором V0равно нулю, получаем зависимость v = at, где перемещение численно равно заштрихованной площади (рис. 10).
Отсюда
Если же v0 не равно 0, то перемещение будет равно площади трапеции, которая может быть представлена суммой площадей прямоугольника и треугольника (рис. 11).
Нетрудно доказать, что
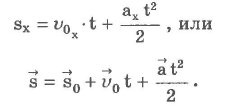
Если перемещение по оси Ох представить как (х - х0), то получим:
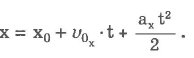
Для определения вида движения следует применить прежнее правило: если совпадают знаки у v0 и ах - движение равноускоренное, в противном случае - движение в начальный момент является равнозамедленным.
Указание на начальный момент означает, что при несовпадении знаков у v0 и ах рано или поздно движение все же станет равноускоренным, так как изменение скорости приведет в конечном итоге к тому, что ускорение и скорость будут совпадать по направлению. Например, при движении брошенного вверх тела сначала его скорость по своему направлению противоположна ускорению свободного падения. Движение при этом будет равнозамедленным. Скорость убывает, становится равной нулю и затем меняет свое направление (после того, как тело достигнет наивысшей точки полета). Далее движение становится равноускоренным.
При этом ускорение остается величиной постоянной и по модулю, и по направлению. Сформулируем основную и обратную задачи механики. Основная задача. Определить местоположение материальной точки в любой заданный момент времени. Чтобы ее решить, необходимо составить уравнения движения: х = ft(t); у = f2(t); z = f3(t).
Обратная задача. Зная местоположение тела в любой заданный момент времени, определить характеристики его движения (v и a). Графически равнопеременное прямолинейное движение можно изобразить графиком зависимости проекции ускорения от времени (рис. 12).
Движения 1, 2, 3 являются равнопеременными. Не зная начальных скоростей, нельзя судить о том, являются ли эти движения равнозамедленными или равноускоренными.
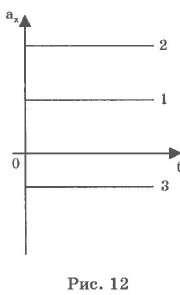
Ясно только одно: а1 и а2 совпадают по направлению с выбранной осью Ох, а а3 направлено в противоположную сторону. Графики скорости дают более конкретные сведения о движении тела (рис. 13): Движения 1 и 2 - равноускоренные с ускорениями а2>а,. Движения 3 и 4 - равнозамедленные с ускорениями а3 > а4
Из графика зависимости проекции скорости от времени можно получить более точные сведения о движении.
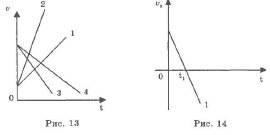
Так, из рис. 14 видно, что при равнозамедленном движении проекция скорости vх при времени t1 обратилась в ноль, а затем модуль скорости стал возрастать, а знак проекции изменился, следовательно, движение с этого момента стало равноускоренным.
Нетрудно заметить, что на графике скорости ускорение будет равно тангенсу угла наклона графика к оси времени (рис. 14).
Поскольку в уравнение проекции перемещения (координаты) время входит во второй степени, то соответствующий график должен быть параболой (рис. 15).
Проанализируем различные движения, отображенные на графиках х = f(t) (рис. 15 и 16).
Графики на рис. 15 соответствуют условиям:
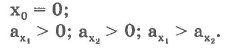
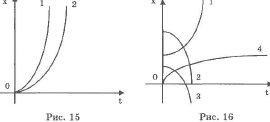
При более общих условиях возможны следующие случаи (рис. 16):
- Движение равноускоренное: ах > 0; v0x > 0; х0 > 0.
- Движение равноускоренное: ах < 0; v0x < 0; х0 > 0.
- Движение равноускоренное: ах < 0; v0x, < 0; х0 > 0.
- Движение равнозамедленное: v0x > 0; ах < 0, конечная координата не меняется с течением времени, что означает остановку.













Комментарии: (0)