Движение тела, брошенного под углом к горизонту
Основные формулы криволинейного движения
1. Скорость движения материальной точки
\(\vec V=\frac{d\vec r}{dt}\),
где \(\vec r\) - радиус-вектор точки.
2. Ускорение материальной точки
\(\vec a=\frac{d\vec V}{dt}=\frac{d^2\vec r}{dt^2}\),
\(a=\sqrt{a^2_{\tau}+a^2_n}\),
где \(a_{\tau}\) - тангенциальное ускорение, \(a_n\) - нормальное ускорение.
3. Тангенциальное ускорение
\(a_{\tau}=\frac{dV}{dt}=\frac{d^2s}{dt^2}\)
4. Нормальное ускорение
\(a_n=\frac{V^2}{R}\),
где \(R\) - радиус кривизны траектории.
5. для равнопеременного движения
\(S=V_0t+\frac{at^2}{2}\)
\(V=V_0+at\)
Выразив из второго равенства \(t\) и подставив в первое, получим полезную формулу
\(2aS=V^2-V_0^2\)
Примеры решения задач
В задачах о движении тела в поле силы тяжести будем полагать \(a=g=9.8\) м/с2.
Задача 1.
Снаряд вылетает из орудия с начальной скоростью 490 м/с под углом 300 к горизонту. Найти высоту, дальность и время полета снаряда, не учитывая его вращение и сопротивление воздуха.
Решение задачи
Найти: \(h, S, t\)
Дано:
\(V_0=490\) м/с
\(\alpha=30^0\)
Свяжем ИСО с орудием.
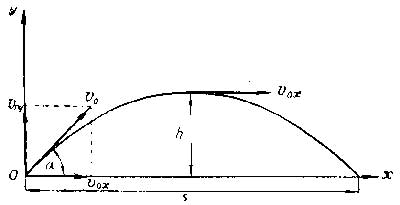
Составляющие скорости по осям Ox и Oy в начальный момент времени равны:
\(V_{0x}=V_0\cos\alpha\) - остается неизменной во все время полета снаряда,
\(V_{0y}=V_0\sin\alpha\) - меняется согласно уравнению равнопеременного движения
\(V_y=V_0\sin\alpha-gt\).
В наивысшей точке подъема \(V_y=V_0\sin\alpha-gt_1=0\), откуда
\(t_1=\frac{V_0\sin\alpha}{g}\)
Полное время полета снаряда
\(t=2t_1=\frac{2V_0\sin\alpha}{g}=50\) c.
Высоту подъема снаряда определим из формулы пути равно замедленного движения
\(h=V_{0y}t_1-\frac{gt_1^2}{2}=\frac{V_0^2\sin^2\alpha}{2g}=3060\) м.
Дальность полета определим как
\(S=V_{0x}t=\frac{V_0^2\sin{2\alpha}}{g}=21000\) м.
Задача 2.
Из точки А свободно падает тело. Одновременно из точки В под углом \(\alpha\) к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол \(\alpha\) не зависит от начальной скорости \(V_0\) тела, брошенного из точки В, и определить этот угол, если \(\frac{H}{S}=\sqrt3\). Сопротивлением воздуха пренебречь.
Решение задачи.
Найти: \(\alpha\)
Дано: \(\frac{H}{S}=\sqrt3\)
Свяжем ИСО с точкой В.
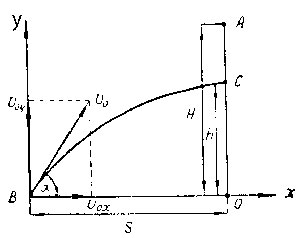
Оба тела могут встретиться на линии ОА (см. рис.) в точке С. Разложим скорость \(V_0\) тела, брошенного из точки В, на горизонтальную и вертикальную составляющие:
\(V_{0x}=V_0\cos\alpha\); \(V_{0y}=V_0\sin\alpha\).
Пусть от начала движения до момента встречи пройдет время
\(t=\frac{S}{V_{0x}}=\frac{S}{V_0\cos\alpha}\).
За это время тело из точки А опуститься на величину
\(H-h=\frac{gt^2}{2}\),
а тело из точки В поднимется на высоту
\(h=V_{0y}t-\frac{gt^2}{2}=V_0\sin\alpha{t}-\frac{gt^2}{2}\).
Решая последние два уравнения совместно, находим
\(H=V_0\sin\alpha{t}\).
Подставляя сюда ранее найденное время, получим
\(\tan\alpha=\frac{H}{S}=\sqrt3\),
т.е. угол бросания не зависит от начальной скорости.
\(\alpha=60^0\)
Задача 3.
С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Решение задачи.
Найти: \(\alpha\)
Дано: \(V_0=40\) м/с. \(t=3\) c.
Свяжем ИСО с башней.
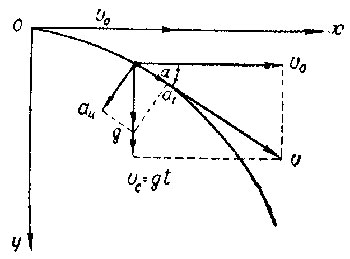
Тело одновременно участвует в двух движениях: равномерно в горизонтальном направлении со скоростью \(V_0\) и в свободном падении со скоростью \(V_y=gt\). Тогда полная скорость тела есть
\(V=\sqrt{V_0^2+g^2t^2}=50 м/с.\)
Направление вектора скорости определяется углом \(\alpha\). Из рисунка видим, что
\(\cos\alpha=\frac{V_0}{V}=\frac{V_0}{\sqrt{V_0^2+g^2t^2}}=0.8\)
\(\alpha=37^0\)
Задача 4.
Два тела брошены вертикально вверх из одной точки одно вслед за другим с интервалом времени, равным \(\Delta{t}\), с одинаковыми скоростями \(V_0\). Через какое время \(t\) после бросания первого тела они встретятся?
Решение задачи.
Найти: \(t\)
Дано: \(V_0\), \(\Delta{t}\)
Из анализа условия задачи, ясно, что первое тело поднимется на максимальную высоту и на спуске встретится со вторым телом. Запишем законы движения тел:
\(h_1=V_0t-\frac{gt^2}{2}\)
\(h_2=V_0(t-\Delta{t})-\frac{g(t-\Delta{t})^2}{2}\).
В момент встречи \(h_1=h_2\), откуда сразу получаем
\(t=\frac{V_0}{g}+\frac{\Delta{t}}{2}\)













Комментарии: (0)