Решение задачи о сложении нескольких сил, направленных под углом друг к другу, начнем со случая, когда на тело действуют только две силы, не лежащие на одной прямой. В этом случае, как показывает опыт, равновесие тела невозможно; значит, равнодействующая таких сил не может равняться нулю. Например, на тело, подвешенное на нити, действует вертикально сила тяжести, и если нить (а значит, и сила натяжения нити) расположена наклонно к вертикали, то тело не остается в покое. На этом основано устройство отвеса.
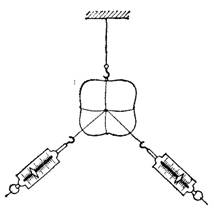
Рис. 64. Если динамометры растянуты, то равновесие груза при вертикальном положении нити невозможно
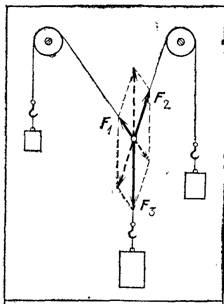
Рис. 65. Условия равновесия трех сил, действующих под углом друг к другу
Другой пример: к телу, подвешенному на нити, прикрепим два динамометра, расположенных горизонтально под углом друг к другу (рис. 64). Легко проверить на опыте, что и в этом случае тело не останется в покое и нить не будет вертикальной ни при каком растяжении динамометров.
Найдем равнодействующую двух сил, направленных под углом друг к другу. Так как равнодействующая равна по модулю и противоположна по направлению уравновешивающей силе (§ 39), то для решения задачи достаточно найти условия равновесия тела под действием трех сил (двух данных и третьей уравновешивающей). Для нахождения этих условий поставим опыт, в котором модули и направления всех сил легко определить. Свяжем три нити, привяжем к ним разные грузы и перекинем две из нитей через блоки (рис. 65). Если масса каждого из грузов меньше суммы масс двух других, то узел займет некоторое положение и будет оставаться в покое; значит, это положение будет положением равновесия. При этом все нити расположатся в одной вертикальной плоскости. На узел действуют силы![]() ,
, ![]() и
и![]() , равные по модулю силам тяжести, действующим на грузы, и направленные вдоль нитей. Каждая из этих сил уравновешивает две остальные. Изобразим силы, приложенные к узлу, отрезками, отложенными от узла, направленными вдоль нитей и равными, в выбранном масштабе, модулям сил. Оказывается, что при равновесии отрезок, изображающий любую из этих сил, совпадает с диагональю параллелограмма, построенного на отрезках, изображающих две другие силы. Эти параллелограммы показаны на рисунке штриховыми линиями. Значит, диагональ параллелограмма изображает равнодействующую двух сил, изображаемых его сторонами, причем равнодействующая направлена в сторону, противоположную третьей силе. Таким образом, силы складываются (как и перемещения) по правилу параллелограмма, т. е. по правилу векторного сложения.
, равные по модулю силам тяжести, действующим на грузы, и направленные вдоль нитей. Каждая из этих сил уравновешивает две остальные. Изобразим силы, приложенные к узлу, отрезками, отложенными от узла, направленными вдоль нитей и равными, в выбранном масштабе, модулям сил. Оказывается, что при равновесии отрезок, изображающий любую из этих сил, совпадает с диагональю параллелограмма, построенного на отрезках, изображающих две другие силы. Эти параллелограммы показаны на рисунке штриховыми линиями. Значит, диагональ параллелограмма изображает равнодействующую двух сил, изображаемых его сторонами, причем равнодействующая направлена в сторону, противоположную третьей силе. Таким образом, силы складываются (как и перемещения) по правилу параллелограмма, т. е. по правилу векторного сложения.
Из правила параллелограмма сил следует, что модуль равнодействующей силы зависит не только от модулей слагаемых сил, но также и от угла между их направлениями. При изменении угла модель равнодействующей изменяется в пределах от суммы модулей сил (если угол равен нулю) до разности модулей большей и меньшей сил (если угол равен 180°). В частном случае сложения двух равных по модулю сил можно, в зависимости от угла между силами, получить любое значение модуля равнодействующей в пределах от удвоенного модуля одной из сил до нуля.
Вместо правила параллелограмма можно применять правило треугольника, как мы это делали для перемещений. При сложении более чем двух сил можно либо прибавлять их векторно одну за другой, либо строить из векторов ломаную; тогда равнодействующая изобразится звеном, замыкающим ломаную. При равновесии ломаная замкнется: равнодействующая будет равна нулю. Например, ломаная из трех уравновешивающихся сил образует треугольник.











Комментарии: (0)