В § 2 мы объяснили, что одно и то же движение тела имеет различный характер в зависимости от того, к какой системе отсчета отнесено это движение. Рассмотрим случай, когда одна из систем отсчета движется относительно другой поступательно. Ясно, что в этом случае вторая система движется относительно первой также поступательно.
Для примера возьмем за такие системы отсчета Землю и железнодорожную платформу, движущуюся по прямому участку пути. Пусть по платформе идет человек. Как, зная движение человека относительно платформы и движение платформы относительно Земли, найти движение человека относительно Земли?
Если перемещение человека относительно платформы изображается вектором
![]() , а перемещение платформы относительно Земли изображается вектором
, а перемещение платформы относительно Земли изображается вектором
![]() , то, как видно из рис. 52, перемещение человека относительно Земли изобразится вектором
, то, как видно из рис. 52, перемещение человека относительно Земли изобразится вектором
![]() , представляющим собой диагональ параллелограмма, построенного на векторах
, представляющим собой диагональ параллелограмма, построенного на векторах
![]() и
и
![]() как на сторонах; это значит, что выполняется векторное равенство
как на сторонах; это значит, что выполняется векторное равенство
![]() (28.1)
(28.1)
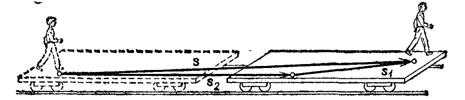
Рис. 52. Сложение перемещений при движениях относительно разных систем отсчета
Так же можно найти перемещение тела и в других случаях: можно показать, что при переходе от одной системы отсчета к другой перемещение тела и перемещение системы отсчета складываются векторно.
Если движение человека относительно платформы и движение платформы относительно Земли — прямолинейные и равномерные, то движение человека относительно Земли также будет прямолинейным и равномерным. В этом случае, разделив обе части равенства (28.1) на промежуток времени
![]() , в течение которого произошли перемещения, найдем
, в течение которого произошли перемещения, найдем
![]() (28.2)
(28.2)
где
![]() — скорость человека относительно платформы,
— скорость человека относительно платформы,
![]() — скорость платформы относительно Земли и
— скорость платформы относительно Земли и![]() — скорость человека относительно Земли. Значит, в этом случае скорость тела и скорость системы отсчета также складываются векторно.
— скорость человека относительно Земли. Значит, в этом случае скорость тела и скорость системы отсчета также складываются векторно.
Можно доказать, формула (28.2) справедлива и для неравномерных движений, если под величинами![]() понимать мгновенные скорости тела и системы отсчета.
понимать мгновенные скорости тела и системы отсчета.
Если платформа движется равномерно и прямолинейно, то, как бы ни двигался человек по платформе, его скорость относительно Земли будет отличаться от скорости относительно платформы только постоянной добавкой
![]() . Значит, все изменения скорости человека будут одинаковы в обеих системах, а значит, одинаковы будут и ускорения человека относительно обеих систем.
. Значит, все изменения скорости человека будут одинаковы в обеих системах, а значит, одинаковы будут и ускорения человека относительно обеих систем.
Итак, если две системы отсчета движутся поступательно, равномерно и прямолинейно относительно друг друга, то ускорения тел относительно обеих систем отсчета будут равны. Скорости же движения тел относительно обеих систем, конечно, будут различны.
28.1. Покажите, что если человек движется относительно платформы прямолинейно, но неравномерно, а платформа движется относительно Земли прямолинейно и равномерно, то человек может двигаться относительно Земли криволинейно.
28.2. За три часа пловец проплывает в стоячей воде 3 км, а бревно вниз по течению — 1 км. Какое расстояние проплывет пловец против течения за это же время?
28.3. Пароход идет вниз по течению от пункта А к пункту В 2 ч, а вверх по течению — 3 ч. Сколько времени будет плыть бревно от пункта А к пункту В?
28.4. Чтобы проплыть некоторое расстояние вниз по течению на лодке, требуется времени втрое меньше, чем вверх по течению. Во сколько раз скорость лодки больше скорости течения?
28.5. Поезд проходит за 15 с мимо телеграфного столба и за 45 с проходит туннель, имеющий длину 450 м. При встрече с поездом длины 300 м оба поезда идут один мимо другого в течение 21 с. Найдите скорость второго поезда.
28.6. Гусеничный трактор движется со скоростью 5 м/с. С какой скоростью движется относительно Земли: а) верхняя часть гусеницы; б) нижняя часть гусеницы? Каковы скорости этих частей гусеницы относительно трактора?
28.7. Моторная лодка развивает в стоячей воде скорость 10 км/ч. Течение реки имеет скорость 5 км/ч. Сколько времени затратит лодка, чтобы пройти вверх по течению 10 км и спуститься обратно на то же место?













Комментарии: (0)