Любой вектор можно представить как сумму нескольких векторов. Например, перемещение тела можно представить как результат нескольких последовательных перемещений, переводящих тело из того же начального в то же конечное положение. Замену одного вектора векторной суммой нескольких других называют разложением вектора на составляющие. Составляющие вектора, конечно, тоже векторы. Разложение вектора на составляющие можно произвести бесконечным числом способов. Можно, например, разложить вектор по двум данным направлениям. Тогда разлагаемый вектор будет служить диагональю параллелограмма, а с заданными направлениями составляющих совпадут стороны параллелограмма (рис. 43).

Рис. 43. Разложение скорости самолета, набирающего высоту, на вертикальную и горизонтальную составляющие
Если задать направление только одной составляющей, то задача о разложении вектора не будет иметь определенного ответа; на рис. 44 мы видим, что можно построить сколько угодно параллелограммов с заданной диагональю (разлагаемый вектор) и заданным направлением одной стороны (направление одной из составляющих).
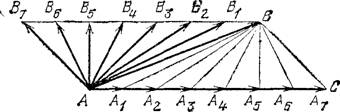
Рис. 44. Разложение вектора ![]() , в котором задано только направление
, в котором задано только направление
![]() одной составляющей. Вектор
одной составляющей. Вектор
![]() может быть представлен как суммы векторов
может быть представлен как суммы векторов
![]() и
и
![]() ,
,
![]() и
и
![]() ,
,
![]() и
и
![]() и т. д.
и т. д.
Задача: 24.1. Самолет должен приземлиться в пункте А, лежащем в 300 км к юго-западу от аэродрома вылета, но предварительно он должен сбросить вымпел над аэродромом В, лежащим в 400 км к юго-востоку от аэродрома вылета, Чему равен модуль перемещения
?
Чаще всего производят разложение векторов по направлениям осей какой-либо прямоугольной системы координат (рис. 45, а). На рис. 45, б изображен вектор \(a\) (он же
![]() ). Проведем из точек А и В перпендикуляры к осям
). Проведем из точек А и В перпендикуляры к осям
![]() и
и
![]() .Точка пересечения перпендикуляра с осью называется проекцией соответствующей точки (A или В) на данную ось (
.Точка пересечения перпендикуляра с осью называется проекцией соответствующей точки (A или В) на данную ось (
![]() или
или
![]() ). На рисунке указаны координаты этих проекций. Разность
). На рисунке указаны координаты этих проекций. Разность
![]() обозначается
обозначается
![]() и называется проекцией вектора \(a\) на ось
и называется проекцией вектора \(a\) на ось
![]() ; аналогично, разность
; аналогично, разность
![]() обозначается
обозначается
![]() и называется проекцией вектора \(a\) на ось
и называется проекцией вектора \(a\) на ось
![]() . Проекции называют также компонентами вектора по координатным осям (
. Проекции называют также компонентами вектора по координатным осям (
![]() — компонента вектора \(a\) по оси
— компонента вектора \(a\) по оси
![]() и т. д.). Проекции (компоненты) являются скалярами.
и т. д.). Проекции (компоненты) являются скалярами.
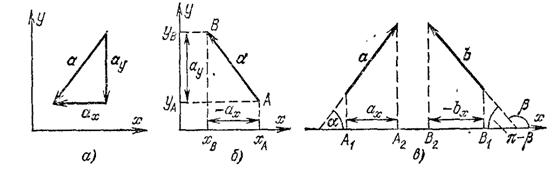
Рис. 45. а) Пример разложения вектора на составляющие, параллельные координатным осям. б) и в) Проекции вектора на координатные оси
Для вектора, изображенного на рис. 45, б,
![]() , вследствие чего проекция на ось
, вследствие чего проекция на ось
![]() отрицательна
отрицательна
![]() ; поскольку
; поскольку
![]() , проекция на ось
, проекция на ось
![]() положительна
положительна
![]() . На рис. 45, б показаны длины отрезков, заключенных между проекциями на ось начала и конца вектора. Эти длины должны выражаться положительными числами. Поэтому значение длины отрезка между проекциями точек А и В на ось
. На рис. 45, б показаны длины отрезков, заключенных между проекциями на ось начала и конца вектора. Эти длины должны выражаться положительными числами. Поэтому значение длины отрезка между проекциями точек А и В на ось
![]() указано в виде
указано в виде
![]() (само
(само
![]() ). Отметим, что проекция вектора \(a\), изображенного на рис. 45, в, положительна, а проекция вектора \(b\) отрицательна.
). Отметим, что проекция вектора \(a\), изображенного на рис. 45, в, положительна, а проекция вектора \(b\) отрицательна.
Дадим еще одно определение проекции вектора. На рис. 45, в показаны векторы \(a\) и \(b\) и их проекции на произвольную ось
![]() . Проекция вектора \(a\) (т. е.
. Проекция вектора \(a\) (т. е.
![]() ) равна длине отрезка
) равна длине отрезка
![]() , взятой со знаком плюс (так как
, взятой со знаком плюс (так как
![]() ); проекция вектора \(b\) (т. е.
); проекция вектора \(b\) (т. е.
![]() ) равна длине отрезка
) равна длине отрезка
![]() , взятой со знаком минус (так как
, взятой со знаком минус (так как
![]() ). Напомним, что на рисунке проставлена длина отрезка
). Напомним, что на рисунке проставлена длина отрезка
![]() , которая выражается положительным числом, равным
, которая выражается положительным числом, равным
![]() .
.
Из рис. 45, в видно, что длина отрезка
![]() (т. е.
(т. е.
![]() ) равна длине отрезка, изображающего вектор \(a\) (т. е. модулю вектора \(a\) ), умноженной на косинус угла
) равна длине отрезка, изображающего вектор \(a\) (т. е. модулю вектора \(a\) ), умноженной на косинус угла
![]() между направлением оси
между направлением оси
![]() и направлением вектора. Следовательно,
и направлением вектора. Следовательно,
![]() . Длина отрезка
. Длина отрезка
![]() равна длине отрезка, изображающего вектор \(b\) (т. е. модулю вектора \(b\) ), умноженной на косинус угла
равна длине отрезка, изображающего вектор \(b\) (т. е. модулю вектора \(b\) ), умноженной на косинус угла
![]() . Проекция вектора \(b\) равна этой длине, взятой со знаком минус. Следовательно,
. Проекция вектора \(b\) равна этой длине, взятой со знаком минус. Следовательно,
![]() .
.
Таким образом, независимо от того, какой угол образует направление вектора с направлением оси
![]() , проекция вектора на ось определяется формулой
, проекция вектора на ось определяется формулой
|
|
Если
![]() , то
, то
![]() , если
, если
![]() , то
, то
![]() . При
. При
![]() проекция вектора равна нулю.
проекция вектора равна нулю.
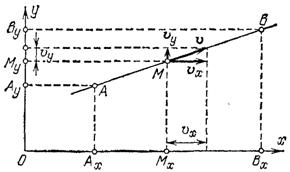
Рис. 46. Проектирование движения точки М на оси координат
Очевидно, что модуль и направление вектора (а следовательно, и сам вектор) полностью определяются заданием проекций вектора на координатные оси. В частности, для векторов, лежащих в плоскости
![]() , модуль определяется формулой
, модуль определяется формулой
![]() . «Длины» и знаки проекций определяют направление вектора.
. «Длины» и знаки проекций определяют направление вектора.
Пусть какая-либо точка движется по прямой. Выберем какую-нибудь систему координат
![]() и спроектируем движущуюся точку на оси координат (рис. 46). На рисунке показаны проекции
и спроектируем движущуюся точку на оси координат (рис. 46). На рисунке показаны проекции
![]() и
и
![]() точки, занимающей в данный момент положение
точки, занимающей в данный момент положение
![]() . При движении точки будут двигаться и ее проекции. Если точка
. При движении точки будут двигаться и ее проекции. Если точка
![]() совершила перемещение
совершила перемещение
![]() , то за то же время ее проекции совершили перемещения
, то за то же время ее проекции совершили перемещения
![]() ,
,
![]() по соответственным осям. Из построения видно, что проекции перемещения движущейся точки
по соответственным осям. Из построения видно, что проекции перемещения движущейся точки
![]() равны перемещениям ее проекций
равны перемещениям ее проекций
![]() и
и
![]() по осям координат. Если точка двигалась равномерно, то проекции также двигались равномерно. Разделив перемещения точки и ее проекций на время
по осям координат. Если точка двигалась равномерно, то проекции также двигались равномерно. Разделив перемещения точки и ее проекций на время
![]() движения точки, найдем скорости
движения точки, найдем скорости
![]() и
и
![]() точки
точки
![]() и ее проекций
и ее проекций
![]() и
и
![]() .
.
Можно показать, что проекция скорости точки равна скорости движения ее проекции. Точно так же можно показать, что при неравномерном движении точки по прямой проекции ее мгновенной скорости и ускорения равны мгновенным скоростям и ускорениям ее проекций. Обратно, если известны перемещения, скорости или ускорения проекций движущейся точки на оси координат, то можно найти перемещение, скорость или ускорение, складывая получившиеся составляющие искомого вектора по правилу параллелограмма.
Таким образом, вместо того чтобы рассматривать движение точки в произвольном направлении, мы всегда можем рассматривать движение только вдоль определенных прямых — осей координат. В ряде случаев выбор осей подсказывается самими условиями задачи. Например, изучая движение брошенного тела, удобно выбрать ось координат по вертикали и но горизонтали.











Комментарии: (0)