Задачи на движение тела, брошенного под углом к горизонту

 3361 сообщений
3361 сообщенийhttp://alexandr4784.narod.ru/
Откуда: Псков
Кто: книгоиздательство
Движение тела, брошенного под углом к горизонту
Основные формулы криволинейного движения
1. Скорость движения материальной точки
\(\vec V=\frac{d\vec r}{dt}\),
где \(\vec r\) - радиус-вектор точки.
2. Ускорение материальной точки
\(\vec a=\frac{d\vec V}{dt}=\frac{d^2\vec r}{dt^2}\),
\(a=\sqrt{a^2_{\tau}+a^2_n}\),
где \(a_{\tau}\) - тангенциальное ускорение, \(a_n\) - нормальное ускорение.
3. Тангенциальное ускорение
\(a_{\tau}=\frac{dV}{dt}=\frac{d^2s}{dt^2}\)
4. Нормальное ускорение
\(a_n=\frac{V^2}{R}\),
где \(R\) - радиус кривизны траектории.
5. для равнопеременного движения
\(S=V_0t+\frac{at^2}{2}\)
\(V=V_0+at\)
Выразив из второго равенства \(t\) и подставив в первое, получим полезную формулу
\(2aS=V^2-V_0^2\)
Примеры решения задач
В задачах о движении тела в поле силы тяжести будем полагать \(a=g=9.8\) м/с2.
Задача 1.
Снаряд вылетает из орудия с начальной скоростью 490 м/с под углом 300 к горизонту. Найти высоту, дальность и время полета снаряда, не учитывая его вращение и сопротивление воздуха.
Решение задачи
Найти: \(h, S, t\)
Дано:
\(V_0=490\) м/с
\(\alpha=30^0\)
Свяжем ИСО с орудием.
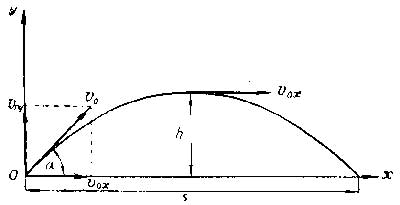
Составляющие скорости по осям Ox и Oy в начальный момент времени равны:
\(V_{0x}=V_0\cos\alpha\) - остается неизменной во все время полета снаряда,
\(V_{0y}=V_0\sin\alpha\) - меняется согласно уравнению равнопеременного движения
\(V_y=V_0\sin\alpha-gt\).
В наивысшей точке подъема \(V_y=V_0\sin\alpha-gt_1=0\), откуда
\(t_1=\frac{V_0\sin\alpha}{g}\)
Полное время полета снаряда
\(t=2t_1=\frac{2V_0\sin\alpha}{g}=50\) c.
Высоту подъема снаряда определим из формулы пути равно замедленного движения
\(h=V_{0y}t_1-\frac{gt_1^2}{2}=\frac{V_0^2\sin^2\alpha}{2g}=3060\) м.
Дальность полета определим как
\(S=V_{0x}t=\frac{V_0^2\sin{2\alpha}}{g}=21000\) м.
Задача 2.
Из точки А свободно падает тело. Одновременно из точки В под углом \(\alpha\) к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол \(\alpha\) не зависит от начальной скорости \(V_0\) тела, брошенного из точки В, и определить этот угол, если \(\frac{H}{S}=\sqrt3\). Сопротивлением воздуха пренебречь.
Решение задачи.
Найти: \(\alpha\)
Дано: \(\frac{H}{S}=\sqrt3\)
Свяжем ИСО с точкой В.
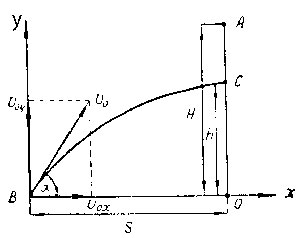
Оба тела могут встретиться на линии ОА (см. рис.) в точке С. Разложим скорость \(V_0\) тела, брошенного из точки В, на горизонтальную и вертикальную составляющие:
\(V_{0x}=V_0\cos\alpha\); \(V_{0y}=V_0\sin\alpha\).
Пусть от начала движения до момента встречи пройдет время
\(t=\frac{S}{V_{0x}}=\frac{S}{V_0\cos\alpha}\).
За это время тело из точки А опуститься на величину
\(H-h=\frac{gt^2}{2}\),
а тело из точки В поднимется на высоту
\(h=V_{0y}t-\frac{gt^2}{2}=V_0\sin\alpha{t}-\frac{gt^2}{2}\).
Решая последние два уравнения совместно, находим
\(H=V_0\sin\alpha{t}\).
Подставляя сюда ранее найденное время, получим
\(\tan\alpha=\frac{H}{S}=\sqrt3\),
т.е. угол бросания не зависит от начальной скорости.
\(\alpha=60^0\)
Задача 3.
С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Решение задачи.
Найти: \(\alpha\)
Дано: \(V_0=40\) м/с. \(t=3\) c.
Свяжем ИСО с башней.
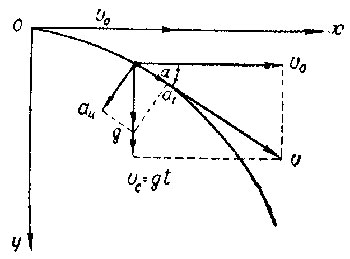
Тело одновременно участвует в двух движениях: равномерно в горизонтальном направлении со скоростью \(V_0\) и в свободном падении со скоростью \(V_y=gt\). Тогда полная скорость тела есть
\(V=\sqrt{V_0^2+g^2t^2}=50 м/с.\)
Направление вектора скорости определяется углом \(\alpha\). Из рисунка видим, что
\(\cos\alpha=\frac{V_0}{V}=\frac{V_0}{\sqrt{V_0^2+g^2t^2}}=0.8\)
\(\alpha=37^0\)
Задача 4.
Два тела брошены вертикально вверх из одной точки одно вслед за другим с интервалом времени, равным \(\Delta{t}\), с одинаковыми скоростями \(V_0\). Через какое время \(t\) после бросания первого тела они встретятся?
Решение задачи.
Найти: \(t\)
Дано: \(V_0\), \(\Delta{t}\)
Из анализа условия задачи, ясно, что первое тело поднимется на максимальную высоту и на спуске встретится со вторым телом. Запишем законы движения тел:
\(h_1=V_0t-\frac{gt^2}{2}\)
\(h_2=V_0(t-\Delta{t})-\frac{g(t-\Delta{t})^2}{2}\).
В момент встречи \(h_1=h_2\), откуда сразу получаем
\(t=\frac{V_0}{g}+\frac{\Delta{t}}{2}\)

А как будет двигаться тело, брошенное со скоростью 20м/сек в сторону центра земли с борта геостационарного спутника?
Могут маги, я могу.
#24714 Борис Попов :А как будет двигаться тело, брошенное со скоростью 20м/сек в сторону центра земли с борта геостационарного спутника?
Однозначно, по эллипсу, с периодической встречей этого спутника в точке пересечения орбит.
Но это отдельная тема, а тут это офтоп.
Не стоит тут этого продолжать, это не та беседка где общаются, тут просто подборка формул для студентов.
Уважаемый Борис Попов
если хотите пообщаться, то по данному вопросу, коль он вам очень интересен, заведите новую тему, с соответствующим названием, о баллистике тел на орбитах.
О том, можно ли запустить спутник на орбиту непосредственно с поверхности Земли минуя её корректировку (например, запуск спутника выстрелом из пушки).
Реально ли воспроизвести выстрел Мюнхаузена. который Барон с полётом на Луну и тд
отредактировал(а) VladimirSS: 2017-07-25 16:58 GMT

VladimirSS #24717 2017-07-23 21:49 GMT Однозначно, по эллипсу, с периодической встречей этого спутника в точке пересечения орбит.
А как это движение будет выглядеть для космонавта, находящегося на борту геостационарного спутника?
Могут маги, я могу.

Точнее задача бросания предмета с башни рещается при ИСО центр Земли. Уситывактся разность линейных скоростей основания и верха башни. На форумах с этим много путаницы.

Скажите, а по какой формуле можно расчитать время и скорость вертикального падения, например градинки 500 -1000 микрон из стратосферы?
Здесь вероятно большую роль должна играть меняющаяся плотность атмосферы. И не знаю будет ли иметь большое влияние меняющаяся сила гравитации.
(в идеальных условиях, без учета всяких сложных вихревых воздействий ) .
Спасибо.
отредактировал(а) Sergey Tree: 2020-08-12 20:24 GMT

Здравствуйте. kstu.kz

#38801 Sergey Tree : Скажите, по какой формуле можно расчитать время и скорость вертикального падения, например градинки 500 -1000 микрон из стратосферы?
Ни по какой. Вы не задали условие задачи. Набор слов который вы даете не является условием задачи.
Градина может растаять в воздуе и не долететь до земли. Превратиться в каплю воды, испариться. Есть столкновения градин.Она может слипнуться с другой или разбиться на части.
В таких случаях сначало составляется набор возможных вариантов решения. Например 16 вариантов. Из низ 7 вариантов дают вероятность того, что градина долетит до земли.
Используется система интегро-дифференциальных уравнений Больцмана для разряженного газа.
Затем когда плотность воздуха повысится, используется уравнение Навье-Стокса и уравнение энергии.
И численные методы решения на компьютере.
Такие системы очень чувствительны к изменению данных. Поэтому можно рассчитать параметры траектории градины на небольшое расстояние. Их вероятностные величины. С какой вероятностью градина долетит до земли.
Это тоже самое, если бы вы сказали.У меня крупинка сахара. Есть ли формула, которая позволит рассчитат ее падение на дно чашки с горячим чаем?
Нет конечно. Формулы описывают только самые простейшие процессы в природе. Вероятность того, что она не растаяет опустившись на дно равна нулю.
Я изучаю градины под микроскопом. В них иногда пузырьки воздуха. Они напоминают клубок ниток. Т.к. капли наматываются на градину и застывают. Температура в небе от -50С до -100С примерно. Это какой-то особенный вид льда. В Монреале примерно раз в 30 лет бывают градины огромные, которые разбивают стекла автомашин! Здесь очень холодные массы воздуха прилетают с Гренландии, с северо-ледовитого океана. Я впервые увидел на улице голубя, лежащего, еще живого. Он обморозился в воздухе во время бури зимой. Также и капля воды.
отредактировал(а) marsdmitri: 2021-02-27 23:05 GMT

Для образовательных целей напишите программу, которая на экране одновременно рисует траектории двух брошенных тел под разными углами к горизонту.
В какой-то точке они пересекуться, и упадут на землю. Мне очень пригодился навык написания такой программы. На бэйсике, яве, с++, Питоне или каком-то другом языке. Если вы можете написать такую программы, то можете составить множества других и понимаете школьную механику.
как пример
https://www.cyberforum.ru/csharp-beginners/thread1750986.html
https://www.CyberForum.ru/csharp-beginners/thread2112834.html
На Visual Basic
Вам очень пригодится в жизни умение писать такие простые программы с графикой.
Если вы решили задачу попробуйте затем ее промоделировать с графикой.
отредактировал(а) marsdmitri: 2022-06-12 04:54 GMT
#41383 marsdmitri :Для образовательных целей сделайте программу,
Программы НЕ ДЕЛАЮТ, а пишут… делают детей.
«Целкни кобылу в нос — она взмахнет хвостом.»
«Зри в корень» К.Прутков С
Я умею читать мысли других, но только тогда, когда они у них есть

Здравствуйте. В КарТУ все эти задачи решат. kstu.kz

Pдравствуйте. Отлично kstu.kz